CIE RGB

CIE RGB est un espace de couleur défini par la Commission internationale de l'éclairage (CIE) en 1931. Il fait partie de la famille des espaces Rouge Vert Bleu et est l'une des premières tentatives de quantification de la couleur. Ces trois couleurs ont une importance particulière car elles sont proches des maxima de réponse des trois types de cônes de la rétine de l'œil humain. Pour étudier de manière approfondie un tel espace, la CIE a particularisé les trois couleurs primaires par des couleurs pures de longueurs d'onde bien définies.

L'espace CIE RGB est basé sur les expériences menées par John Guild et William David Wright sur la vision humaine dans les années 1920 auprès d'un échantillon de la population dépourvu de défaut visuel.

Les espaces RGB présentent l'inconvénient de recourir à des composantes négatives pour caractériser les couleurs très saturées non-incluses dans le gamut qui prend la forme d'un triangle dans les représentations graphiques. En effet, ils permettent de reproduire ces mêmes couleurs mais seulement en les blanchissant pour en diminuer la saturation. C'est le cas tout particulièrement pour les couleurs pures dont les teintes sont identifiées physiquement par des longueurs d'onde inférieures à 550 nm environ. Pour impliquer toutes les couleurs distinguées par la vision humaine et ainsi échapper au caractère arbitraire d'un espace RGB particulier, la CIE a également défini la même année l'espace CIE XYZ et ainsi fondé la colorimétrie scientifique.

Définition de l'espace CIE RGB

Espace vectoriel des couleurs

Le système visuel humain est composé de trois entrées, les trois stimuli (ou le tristimulus) issus des trois types de cônes photosensibles, et d'une sortie, la couleur, synthèse additive des trois entrées. Du fait de cette trivariance visuelle, on munit un espace vectoriel à trois dimensions d'une base orthonormée dont les vecteurs {P₁}, {P₂} et {P₃}, appelés couleurs primaires, représentent les trois stimuli. Une couleur quelconque peut alors être définie dans cet espace par un vecteur {C} dont les trois coordonnées C₁, C₂ et C₃, appelées composantes trichromatiques, représentent les pondérations des trois stimuli produisant cette couleur. Le module de {C} correspond à la luminosité de la couleur et la direction à sa chromaticité :

$\{C\}\equiv C_{1}\cdot \{P_{1}\}+C_{2}\cdot \{P_{2}\}+C_{3}\cdot \{P_{3}\}.$

La relation est une relation d'équivalence visuelle, notée $\equiv$, sur les stimuli produisant ces couleurs. Elle signifie que les pondérations C₁, C₂ et C₃ des trois stimuli {P₁}, {P₂} et {P₃} produisant la couleur du membre de droite sont équivalents aux pondérations des trois stimuli produisant la couleur {C}. En revanche elle n'implique pas l'égalité des deux spectres des rayonnements électromagnétiques à l'origine de ces deux tristimuli et donc à l'origine de ces deux couleurs (si leurs spectres sont différents on parle de couleurs métamères).

Par ailleurs, tout rayonnement électromagnétique peut se décomposer en une somme de rayonnements monochromatiques pondérés par une fonction chromatique f(λ) représentant le spectre électromagnétique du rayonnement. Cette décomposition du rayonnement étant spectralement identique au rayonnement, elle produit le même tristimulus et donc la même couleur {C} :

$\{C\}\equiv \int _{0}^{\infty }f(\lambda )\cdot \{C_{\lambda }\}\,\mathrm {d} \lambda ,$

où {C_λ} est la couleur pure produite par le rayonnement monochromatique de longueur d'onde λ.

Chaque couleur pure {C_λ} étant produite par un tristimulus particulier :

$\{C_{\lambda }\}\equiv c_{1}(\lambda )\cdot \{P_{1}\}+c_{2}(\lambda )\cdot \{P_{2}\}+c_{3}(\lambda )\cdot \{P_{3}\},$

où c₁(λ), c₂(λ) et c₃(λ) désignent les composantes trichromatiques spectrales, aussi appelées fonctions colorimétriques, déterminées une fois pour toutes par la CIE à partir d'un panel d'observateurs dépourvus de défaut visuel.

À partir de ces égalités, on obtient

$\{C\}\equiv \int _{0}^{\infty }f(\lambda )c_{1}(\lambda )\,\mathrm {d} \lambda \cdot \{P_{1}\}+\int _{0}^{\infty }f(\lambda )c_{2}(\lambda )\,\mathrm {d} \lambda \cdot \{P_{2}\}+\int _{0}^{\infty }f(\lambda )c_{3}(\lambda )\,\mathrm {d} \lambda \cdot \{P_{3}\},$

et par identification avec la première équation, on déduit les composantes trichromatiques C₁, C₂ et C₃ :

${\begin{cases}\displaystyle C_{1}=\int _{0}^{\infty }f(\lambda )c_{1}(\lambda )\,\mathrm {d} \lambda \\\displaystyle C_{2}=\int _{0}^{\infty }f(\lambda )c_{2}(\lambda )\,\mathrm {d} \lambda \\\displaystyle C_{3}=\int _{0}^{\infty }f(\lambda )c_{3}(\lambda )\,\mathrm {d} \lambda .\end{cases}}$

On voit ainsi qu'une fois les fonctions colorimétriques c₁(λ), c₂(λ) et c₃(λ) définies, toute couleur produite par un spectre électromagnétique f(λ) connu peut être représentée par trois nombres en calculant les composantes C₁, C₂ et C₃.

Fonctions colorimétriques

Fonctions colorimétriques r(λ), g(λ) et b(λ) de l'espace CIE RGB. Elles représentent les quantités des trois couleurs primaires nécessaires pour obtenir par superposition une couleur équivalente à la couleur monochromatique de test de longueur d'onde λ.

Durant les années 1920, John Guild et William David Wright menèrent indépendamment une série d'expériences sur la vision humaine qui posèrent les bases de la définition de l'espace de couleurs CIE RGB en 1931. Les travaux de Guild, réalisés entre 1926 et 1928 et publiés en 1931, concernaient sept observateurs, tandis que ceux de Wright, réalisés entre 1928 et 1929 et publiés en 1929, en concernaient dix.

Les expériences utilisaient un écran circulaire de diamètre angulaire 2°, ce qui correspond à l'angle de la fovéa humaine, partie de la rétine où les cônes sont le plus densément présents. Un côté de l'écran était éclairé par une source de lumière monochromatique de test, l'autre était éclairé par trois sources primaires qui se superposaient pour donner lieu à une synthèse additive des couleurs. L'observateur devait ajuster l'intensité des trois sources primaires en faisant varier leur position longitudinale ou en rétrécissant leur flux à l'aide de diaphragmes calibrés, afin de parvenir à une couleur équivalente visuellement à la couleur monochromatique de test de l'autre moitié de l'écran. L'équivalence visuelle n'était pas possible avec toutes les couleurs de tests. Dans ces cas, une des trois sources primaires était retirée de la moitié de l'écran et superposée à la couleur de test de l'autre moitié de l'écran afin d'aboutir à une couleur équivalente à celle issue des deux sources primaires restantes. La quantité de primaire ajoutée à la couleur de test était alors considérée comme négative. De cette façon, l'étendue complète de la perception des couleurs de la vision humaine pouvait être traitée. Trois courbes représentant la quantité de lumière des trois sources primaires furent ainsi tracées en fonction de la longueur d'onde de la couleur monochromatique de test. Ces trois courbes sont les fonctions colorimétriques de l'expérience.

Pour ses expériences, Guild utilisa trois primaires monochromatiques obtenues avec des filtres en gélatine correspondant à des lumières de longueur d'onde 627,7 nm, 542 nm et 461,6 nm. Wright utilisa quant à lui trois primaires monochromatiques de longueurs d'onde 650 nm, 530 nm et 460 nm. Lors du Comité de colorimétrie de la CIE qui se tint en 1931, Guild proposa de choisir de façon définitive des primaires de longueur d'onde

• λ_R = 700 nm (rouge) ;
• λ_G = 546,1 nm (vert) ;
• λ_B = 435,8 nm (bleu).

Bien que difficile à reproduire en 1931, λ_R fut choisie pour la stabilité de la teinte perçue lors de faibles variations de la longueur d'onde autour de cette valeur. λ_G et λ_B furent choisies car elles correspondaient à deux raies d'émission des lampes à vapeur de mercure utilisées comme standard par le National Physical Laboratory, laboratoire où travaillait Guild. Après de longues délibérations, la proposition de Guild fut adoptée, ces primaires devenant les primaires NPL (National Physical Laboratory). Comme les fonctions colorimétriques des expériences de Guild et Wright utilisaient des primaires différentes, les fonctions furent transformées pour correspondre aux primaires NPL puis moyennées, ce qui aboutit à la définition des fonctions colorimétriques r(λ), g(λ) et b(λ) de l'espace CIE RGB. Ces trois fonctions constituent l'observateur de référence CIE 2° ou l'observateur de référence CIE 1931 et établissent un système international de notation des couleurs.

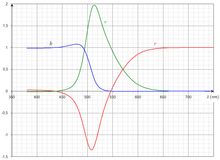
Les fonctions colorimétriques sont les quantités nécessaires des trois couleurs primaires pour obtenir par superposition une couleur équivalente à la couleur monochromatique de test. Ces fonctions sont tracées dans la figure de droite. On remarque que r(λ) et g(λ) sont nulles à λ_B = 435,8 nm, que r(λ) et b(λ) sont nulles à λ_G = 546,1 nm et que g(λ) et b(λ) sont nulles à λ_R = 700 nm, puisque pour ces trois longueurs d'onde la couleur monochromatique de test est la même que l'une des trois primaires. Les trois fonctions colorimétriques sont nulles en dehors de la plage 380 nm (violet extrême) et 780 nm pour le (rouge extrême), ce qui fixe les limites du spectre visible. Ces limites sont fixées quelque peu arbitrairement car l'œil humain est capable de voir jusqu'à 810 nm, mais avec une sensibilité plusieurs milliers de fois inférieure à la sensibilité au vert.

Couleur	Rouge R	Vert G	Bleu B	Blanc E
Longueur d'onde	700,0 nm	546,1 nm	435,8 nm	équi-énergétique
Luminance relative	1	4,590 7	0,060 1	5,650 8

Le blanc de référence est un blanc neutre, c'est-à-dire équi-énergétique (densité spectrale de puissance plate). Expérimentalement, une couleur métamère du blanc équi-énergétique {E} est obtenue lorsqu'on superpose les couleurs primaires rouge {R}, verte {G} et bleue {B} de flux énergétiques (en watts) proportionnels aux valeurs 72,0962 / 1,3791 / 1 respectivement. Ces flux énergétiques correspondent à des flux lumineux (en lumens) proportionnels aux valeurs 1 / 4,5907 / 0,0601 respectivement (cf. le tableau ci-dessus).

Si on normalise les valeurs auxquelles sont proportionnels les flux lumineux de façon à obtenir des valeurs dont la somme est égale à 1, on obtient les valeurs normalisées 0,17697 / 0,81240 / 0,010630 respectivement, qui sont encore trop inégales pour une utilisation pratique. Ceci peut s'expliquer par la grande contribution du bleu et, dans une moindre mesure, du rouge à la sensation colorée, par rapport à leur faible contribution à la luminance. Cela conduit à choisir les luminances de chaque couleur primaire de façon que les composantes R, G et B du blanc {E} soient égales. Pour cela, on affecte aux luminances de chaque couleur primaire les valeurs précédemment trouvées :

${\begin{cases}L_{\mathrm {\{R\}} }=1\ \mathrm {cd} \cdot \mathrm {m} ^{-2}\\L_{\mathrm {\{G\}} }=4{,}590\,7\ \mathrm {cd} \cdot \mathrm {m} ^{-2}\\L_{\mathrm {\{B\}} }=0{,}060\,1\ \mathrm {cd} \cdot \mathrm {m} ^{-2}.\end{cases}}$

Avec cette convention, le blanc {E} a pour composantes R = 1, G = 1 et B = 1, pour coordonnées r = 1/3, g = 1/3 et b = 1/3, et pour luminance

$L_{\mathrm {\{E\}} }=1\cdot L_{\mathrm {\{R\}} }+1\cdot L_{\mathrm {\{G\}} }+1\cdot L_{\mathrm {\{B\}} }=5{,}650\,8\ \mathrm {cd} \cdot \mathrm {m} ^{-2}.$

Cependant les grandeurs utilisées sont souvent des luminances relatives (par rapport au blanc qui est toujours le plus lumineux) et sont donc données sans unité.

Soit un blanc équi-énergétique {E} de luminance énergétique L′_{E} (en W sr⁻¹ m⁻²). La luminance énergétique spectrale S_{E}(λ) (en W sr⁻¹ m⁻² m⁻¹) est définie par

$S_{\mathrm {\{E\}} }(\lambda )={\frac {\Delta L'_{\mathrm {\{E\}} }}{\Delta \lambda }}={\frac {L'_{\mathrm {\{E\}} }}{\lambda _{2}-\lambda _{1}}}.$

Les limites du visible en colorimétrie et en photométrie sont fixées par λ₁ = 380 nm pour le violet extrême et λ₂ = 780 nm pour le rouge extrême.

Le spectre de E est découpé en tranches juxtaposées de largeur ∆λ, correspondant à une couleur quasi-monochromatique, centrées sur la longueur d'onde λ. La luminance énergétique sur chacune de ces bandes vaut ∆L′_{E} = S_{E}(λ)∆λ.

L'égalisation de la sensation colorée d'une tranche ∆λ, est assurée par les composantes trichromatiques ∆R, ∆G et ∆B.

Les fonctions colorimétriques sont alors définies, en fonction de la longueur d'onde centrale λ :

${\begin{cases}{\overline {r}}(\lambda )={\dfrac {\Delta {\overline {R}}(\lambda )}{\Delta \lambda }}\\{\overline {g}}(\lambda )={\dfrac {\Delta {\overline {G}}(\lambda )}{\Delta \lambda }}\\{\overline {b}}(\lambda )={\dfrac {\Delta {\overline {B}}(\lambda )}{\Delta \lambda }}.\end{cases}}$

Les valeurs négatives s'expliquent par le fait qu'il faut ajouter du rouge aux couleurs cyans pures (par exemple) pour pouvoir égaliser la sensation colorée par addition de vert et de bleu. Cela signifie qu'on ne pourra pas obtenir toutes les couleurs visibles à partir de cet espace.

Remarque. — Les fonctions colorimétriques une fois pondérées par le poids des primaires égalisent la fonction d'efficacité lumineuse relative spectrale :

$V(\lambda )=1{,}000\,0\cdot {\overline {r}}(\lambda )+4{,}590\,7\cdot {\overline {g}}(\lambda )+0{,}060\,1\cdot {\overline {b}}(\lambda ).$

Composantes trichromatiques

Les fonctions colorimétriques permettent de reconstituer toute couleur {C} à partir de sa densité spectrale de luminance énergétique S(λ) (en W sr⁻¹ m⁻² m⁻¹). R, G, B sont les composantes trichromatiques de ce stimulus :

$\{C\}\equiv R\cdot \mathrm {\{R\}} +G\cdot \mathrm {\{G\}} +B\cdot \mathrm {\{B\}} .$

Elles peuvent être calculées grâce aux relations

${\begin{cases}R=k\int _{0}^{\infty }{\overline {r}}(\lambda )S(\lambda )\,\mathrm {d} \lambda \\G=k\int _{0}^{\infty }{\overline {g}}(\lambda )S(\lambda )\,\mathrm {d} \lambda \\B=k\int _{0}^{\infty }{\overline {b}}(\lambda )S(\lambda )\,\mathrm {d} \lambda ,\end{cases}}$

où k est une constante de normalisation.

Le choix k = K_m = 683,002 lm/W, l'efficacité lumineuse spectrale maximale, permet d'obtenir des coordonnées R = G = B = 1 pour un blanc équi-énergétique {E} de luminance L_{E} = 5,650 8 cd m⁻².

Ces composantes permettent d'une part de calculer la luminance d'une couleur, d'autre part de déterminer la proportion de chaque couleur primaire utilisée pour reconstituer la couleur {C}.

Luminance

La luminance d'une couleur {C} peut être obtenue à partir de ses composantes trichromatiques R, G, B, connaissant les luminances L_{R}, L_{G}, L_{B} des couleurs primaires. On obtient la formule suivante :

$L_{\{C\}}=1{,}000\,0\cdot R+4{,}590\,7\cdot G+0{,}060\,1\cdot B.$

La nécessité de passer par cette formule pour calculer la luminance rend le standard CIE RGB moins pratique que le standard CIE XYZ.

Coordonnées trichromatiques x, y, z

Les coordonnées trichromatiques r, g, b, sont obtenues à partir des composantes trichromatiques en se ramenant à une couleur de luminance donnée, de façon que la somme des coordonnées soit égale à 1. Elles indiquent les proportions de chacune des primaires :

${\begin{cases}r={\dfrac {R}{R+G+B}}\\g={\dfrac {G}{R+G+B}}\\b={\dfrac {B}{R+G+B}}=1-r-g.\end{cases}}$

Diagramme de chromaticité CIE (r, g)

Diagramme de chromaticité CIE (r, g). La courbe rouge correspond aux couleurs monochromatiques. Elle entoure le domaine des couleurs visibles. Le triangle coloré montre les couleurs qu'on peut reconstituer avec l'espace CIE RGB. Certaines couleurs visibles ne sont pas reconstituables.

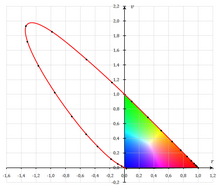
Les coordonnées trichromatiques permettent de représenter les couleurs dans un plan. Le diagramme de chromaticité (r, g) est constitué d'un repère dont l'origine est la primaire bleue (r = g = 0 et donc b = 1), l'axe r des abscisses contient la primaire rouge (r = 1, g = 0 et donc b = 0) et l'axe g des ordonnées contient la primaire verte (r = 0, g = 1 et donc b = 0). Une couleur de coordonnées trichromatiques (r, g, b) est représentée par le point d'abscisse r et d'ordonnée g, la dernière coordonnée b se déduisant des deux autres par la relation b = 1 − r − g. Les couleurs qu'on peut reconstituer dans l'espace CIE RGB forment un triangle.

Coordonnées trichromatiques du lieu du spectre.

Une bande quasi-monochromatique ayant pour composantes r(λ)∆λ, g(λ)∆λ et b(λ)∆λ, il vient que les coordonnées r(λ), g(λ) et b(λ) pour une lumière monochromatique de longueur d'onde λ sont données par

${\begin{cases}r(\lambda )={\dfrac {{\overline {r}}(\lambda )}{{\overline {r}}(\lambda )+{\overline {g}}(\lambda )+{\overline {b}}(\lambda )}}\\g(\lambda )={\dfrac {{\overline {g}}(\lambda )}{{\overline {r}}(\lambda )+{\overline {g}}(\lambda )+{\overline {b}}(\lambda )}}\\b(\lambda )={\dfrac {{\overline {b}}(\lambda )}{{\overline {r}}(\lambda )+{\overline {g}}(\lambda )+{\overline {b}}(\lambda )}}.\end{cases}}$

Diagramme de chromaticité CIE (x, y)

Diagramme dans l'espace CIE RGB montrant la construction du triangle spécifiant l'espace CIE XYZ. Les nouvelles couleurs {X}, {Y}, {Z} sont désignées sur ce graphique par les lettres C_r, C_g, C_b.

Diagramme de chromaticité du système XYZ, et représentation du triangle des couleurs reconstructibles par le système RGB d'un écran d'ordinateur.

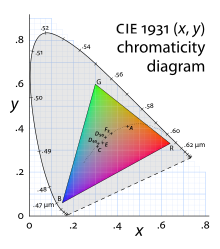
Comme expliqué précédemment, les calculs dans l'espace CIE RGB font intervenir des formules d'emploi malaisé ; l'espace CIE XYZ a été mis au point pour s'affranchir de ces contraintes. Pour cela on choisit trois couleurs fictives dénommées {X}, {Y} et {Z} telles que :

• {X} et {Z} ont une luminance nulle. Cela assurera que, dans le nouvel espace, la luminance sera donnée par la composante selon {Y}.
• Dans le diagramme de chromaticité RGB, {X} et {Y} appartiennent à la tangente en {R} à la courbe des couleurs monochromatiques.
• La droite passant par {X} et {Z} est tangente à la même courbe.
• Le blanc équi-énergétique {E} est égal à {X} + {Y} + {Z}.
• Dans le diagramme de chromaticité RGB, l'aire du triangle défini par {X}, {Y} et {Z}, sous les contraintes précédentes, est d'aire minimale.

L'ensemble des couleurs visibles est alors inclus dans le triangle précédent, de sorte que les fonctions colorimétriques correspondantes sont toutes positives ou nulles. Les formules précises de passage d'un espace à l'autre sont exposées dans l'article détaillé.

Bibliographie

• Alain Pelat, Imagerie et télévision : une introduction : vision – photométrie – colorimétrie, Paris, Ellipses Marketing, 1998, 175 p. (ISBN 2-7298-8826-8)
• Robert Sève, Science de la couleur : Aspects physiques et perceptifs, Marseille, Chalagam, 2009, 374 p. (ISBN 978-2-9519607-5-6 et 2-9519607-5-1)
• Jacques Gaudin, Colorimétrie appliquée à la vidéo, Paris, Dunod, 2006, 278 p. (ISBN 2-10-049515-1)
• (en) Jànos Schanda, Colorimetry : Understanding the Cie System, New Jersey, Wiley-Blackwell, 2007, 459 p. (ISBN 978-0-470-04904-4)

Voir aussi

Articles connexes

• Espace de couleur
• Système ordonné de couleurs

Liens externes

• Calcul des coordonnées du lieu du spectre et des fonctions colorimétriques CIE 1931 RGB à partir des données expérimentales
• CIE Color Space, Gernot Hoffman
• Documents CIE en téléchargement libre
• Comprendre la couleur et maîtriser les profils ICC