Carré des liaisons
Le carré des liaisons est une représentation graphique utile dans l’analyse factorielle d’un tableau individus x variables. Cette représentation complète les représentations classiques de l’Analyse en composantes principales (ACP) et de l’Analyse des correspondances multiples (ACM), à savoir celles des individus, des variables quantitatives (par leur coefficient de corrélation avec les facteurs) et celle des modalités des variables qualitatives (au barycentre des individus qui les possèdent).
Définition en ACM
modifierLe premier intérêt du carré des liaisons est de représenter les variables qualitatives elles-mêmes, et non leurs modalités, ce qui est d’autant plus précieux que les variables sont nombreuses. Pour cela on calcule, pour chaque variable qualitative et chaque facteur (, facteur de rang , est le vecteur des coordonnées des individus le long de l’axe ; en ACP, est appelé composante principale de rang s), le carré du rapport de corrélation entre le facteur et la variable , soit :
Ainsi, à chaque plan factoriel, on peut associer une représentation des variables qualitatives elles-mêmes[1].
Leurs coordonnées étant comprises entre 0 et 1, les variables apparaissent nécessairement dans le carré dont les sommets sont, outre l’origine, les points de coordonnées (0,1), (1,0) et (1,1).
Exemple en ACM
modifierSix individus sont décrits par trois variables qualitatives ayant respectivement, 3, 2 et 3 modalités.
| -a | -d | -f | |
| -b | -d | -f | |
| -c | -d | -g | |
| -a | -e | -g | |
| -b | -e | -h | |
| -c | -e | -h |
Appliquée à ces données, l’ACM du package R FactoMineR conduit au graphique classique de la figure 1.
 |
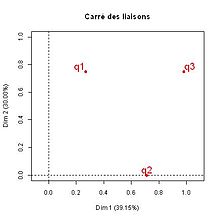 |
Le carré des liaisons (figure 2) aide la lecture du graphique classique. Il indique que :
- Le premier facteur est lié aux trois variables mais surtout à et ensuite à .
- Le deuxième facteur est lié uniquement à et et ce de manière forte et égale.
Tout ceci est, bien sûr, visible sur le graphique classique. Le rôle du carré des liaisons est d’abord d’aider à une lecture structurée du graphique classique.
Extensions
modifierCette représentation peut être complétée par celles de variables quantitatives, les coordonnées de ces dernières étant des carrés de coefficients de corrélation (et non de rapports de corrélation). Le second intérêt du carré des liaisons réside donc dans la possibilité de représenter simultanément des variables quantitatives et qualitatives [2]. Le carré des liaisons peut être construit à partir de n’importe quelle analyse factorielle d’un tableau individus x variables. En particulier, il est (ou devrait être) systématiquement utilisé, outre en ACM, en ACP lorsqu’il y a beaucoup de variables qualitatives supplémentaires et en Analyse Factorielle de Données Mixtes. Une extension de ce graphique aux groupes de variables est utilisée en Analyse Factorielle Multiple (AFM)[3],[4].
Conclusion
modifierEn ACM, le carré des liaisons apporte une visualisation synthétique des liaisons entre facteurs et variables d’autant plus précieuse que les variables sont nombreuses et possèdent beaucoup de modalités.
Notes
modifier- Exemple au sein d'une interprétation d'ACM dans Husson et al 2009, p. 53 et suiv.
- Exemple comportant les deux types de variables dans Pagès 2013, p. 72
- Pagès 2013, p. 125 et suiv.
- Exemple avec des variables et des groupes de variables dans Escofier&Pagès 20o8, p. 161 et suiv.
Bibliographie
modifier- Brigitte Escofier et Jérôme Pagès, Analyses factorielles simples et multiples : objectifs, méthodes et interprétation, Paris, Dunod, Paris, 2008, 4e éd. (1re éd. 1988), 318 p. (ISBN 978-2-10-051932-3)
- François Husson, Sébastien Lê et Jérôme Pagès, Analyse des données avec R, Presses Universitaires de Rennes, , 224 p. (ISBN 978-2-7535-0938-2)
- Jérôme Pagès, Analyse factorielle multiple avec R, Les Ulis, EDP sciences, Paris, , 253 p. (ISBN 978-2-7598-0963-9)
Liens externes
modifierFactoMineR, une bibliothèque de fonctions R destinée à l'analyse des données














