Domaine de Weiss

Un domaine magnétique, ou domaine de Weiss, est une région d'un matériau dans laquelle les moments magnétiques sont orientés dans la même direction, l'orientation de l'aimantation y est donc uniforme. La région séparant les domaines magnétiques est appelée paroi de domaine, dans laquelle l’aimantation change progressivement de direction. Dans un domaine magnétique, les moments magnétiques de chaque atome sont alignés les uns avec les autres et pointent dans la même direction. La structure des domaines magnétiques est responsable du comportement magnétique des matériaux ferromagnétiques comme le fer, le nickel, le cobalt et de leurs alliages, mais cela concerne aussi les matériaux ferrimagnétiques.

Grains microcristallins dans un morceau de NdFeB (alliage utilisé dans les aimants au néodyme) avec des domaines magnétiques rendus visibles grâce à un microscope Kerr. Les domaines sont les rayures claires et foncées visibles dans chaque grain.

Les domaines magnétiques se forment dans des matériaux ayant un ordre magnétique, c’est-à-dire que les dipôles magnétiques du matériau s'alignent spontanément sous l'effet de l’interaction d’échange. Il s’agit des matériaux ferromagnétiques, ferrimagnétiques et antiferromagnétiques. Les matériaux paramagnétiques et diamagnétiques, dans lesquels les dipôles s’alignent en réponse à un champ externe, mais ne s’alignent pas spontanément, n’ont pas de domaines magnétiques.

Développement de la théorie des domaines

La théorie des domaines magnétiques a été développée par le physicien français Pierre-Ernest Weiss qui, en 1906, suggéra l’existence de domaines magnétiques dans les matériaux ferromagnétiques. Il suggéra qu’un grand nombre de moments magnétiques atomiques (environ 10¹² à 10¹⁸) y seraient alignés parallèlement. La direction d’alignement des domaines varie d’un domaine à l’autre d’une manière plus ou moins aléatoire, bien que certains axes cristallographiques, appelés axes de facile aimantation, soient privilégiés par les moments magnétiques. Weiss devait toujours expliquer la raison pour laquelle les moments magnétiques atomiques s’alignaient spontanément au sein d’un matériau ferromagnétique. Il exposa alors sa théorie du champ moyen, plus connue sous son nom anglais : Mean Field Theory. Il supposa dans cette théorie que, dans un matériau, un moment magnétique donné était soumis à un fort champ magnétique dû à l’aimantation de ses voisins. Dans sa théorie initiale, le champ moyen était proportionnel à l’aimantation du matériau M, tel que $H_{e}=\alpha \ M$ où $\alpha \$ est la constante du champ moyen. Cependant, ceci n’est pas applicable au matériau ferromagnétique à cause de la variation d’aimantation d’un domaine à l’autre. Dans ce cas le champ d’interaction est.

$$H_{e}=\alpha \ M_{s}$$

où $M_{s}$ est l’aimantation de saturation à 0 K.

Plus tard, la physique quantique a permis de comprendre l’origine microscopique du champ moyen (ou champ de Weiss). L’interaction d’échange entre spins locaux favorise un alignement parallèle (matériau ferromagnétique) ou antiparallèle (matériau antiferromagnétique) des moments magnétiques voisins.

La structure des domaines

Énergies régissant les matériaux magnétiques dans un champ magnétique extérieur

Les matériaux magnétiques, et notamment les ferromagnétiques, ont une structure qui dépend de plusieurs énergies. L'énergie totale de la structure est donnée par :

$$E_{tot}=E_{ex}+E_{m}+E_{\lambda }+E_{k}+E_{H}\,$$

Avec:

• E_ex est l’énergie d'échange : c'est l'énergie due à l'interaction d'échange entre les sites magnétiques des matériaux ferromagnétiques, ferrimagnétiques et antiferromagnétiques. Dans le cas des matériaux ferromagnétiques, elle est à son minimum quand tous les dipôles sont dirigés dans la même direction, ainsi elle est responsable de l'aimantation des matériaux magnétiques. Quand deux domaines avec différentes directions d'aimantation sont l'un à côté de l'autre, les dipôles magnétiques sont orientés dans différentes directions au sein de la paroi de Bloch ce qui augmente l’énergie d’échange. Cette énergie d'échange supplémentaire est proportionnelle à la surface totale des parois de Bloch.
• E_m est l’énergie magnéto-statique : c'est une auto-énergie due à l'interaction du champ magnétique créé par l'aimantation dans une certaine partie de l'échantillon sur d'autres parties du même échantillon. Elle dépend du volume occupé par le champ magnétique se prolongeant en dehors du domaine magnétique. Cette énergie est réduite en réduisant au minimum la longueur des boucles de lignes de champ magnétique en dehors du domaine. Par exemple, ceci tend à encourager l'aimantation à devenir parallèle aux surfaces de l'échantillon, de telle sorte que les lignes de champ ne passent pas en dehors de l'échantillon. La réduction de cette énergie est la raison principale de l'existence des domaines magnétiques.
• E_λ est l’énergie d'anisotropie magnéto-élastique : cette énergie est due à l'effet de la magnétostriction, qui induit une légère modification des dimensions du cristal une fois aimanté. Ceci implique des tensions élastiques dans le réseau, et la direction de l'aimantation qui réduit au minimum ces énergies de tension sera favorisée. Cette énergie tend à être réduite au minimum quand tous les axes d'aimantation des domaines dans un cristal sont parallèles.
• E_k est l’énergie d'anisotropie magnéto-cristalline : lorsqu'un atome est placé au sein d'un cristal, ses orbitales atomiques subissent une levée de dégénérescence. Par exemple, les orbitales 3d ne sont plus toutes équivalentes : celles dont la forme minimise l'énergie électrostatique due à la présence des ions voisins sont favorisées énergétiquement. Cela conduit à minimiser l'énergie lorsque le moment orbital pointe dans certaines directions du réseau cristallin. La présence du couplage spin-orbite favorise donc certaines directions du moment magnétique total par rapport à d'autres. Le réseau cristallin est facile à aimanter selon une direction et plus difficile selon les autres. Cette énergie est réduite au minimum quand l'aimantation est le long de l'axe choisi (axe de facile aimantation). Ainsi l'aimantation de la plupart des domaines dans un réseau cristallin tend à être dans l'une ou l'autre des directions le long de l'axe de facile aimantation.
• E_H est l’énergie de Zeeman, ou énergie du champ externe : énergie potentielle d'un corps aimanté dans un champ magnétique externe. Elle est due à l'interaction entre le matériau magnétique et un champ magnétique extérieur appliqué.

Existence des domaines magnétiques

L'existence des domaines peut être expliquée par la minimisation de l’énergie totale du matériau donnée précédemment.

La minimisation de l'énergie d'échange explique l'existence de domaine. En effet E_ex dépend du produit scalaire entre deux spins consécutifs donc pour la minimiser il faut que les spins soient tous parallèles les uns aux autres cela implique que dans les domaines les spins sont alignés.

Pour minimiser E_k il faut que les moments magnétiques soient orientés selon les axes de facile aimantation. C'est pourquoi dans un cristal cubique, puisqu’il existe deux axes de faciles aimantation orientés à 90° l'un de l'autre, on peut trouver une configuration telle que celle-ci:

Orientation des domaines d'un cristal à réseau cubique

Mise en évidence de la réduction du champ magnétique lors de l'existence de plusieurs domaines.

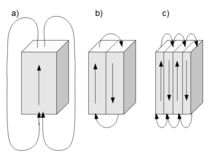
Si l'on néglige l'influence de E_λ, et en l'absence de champ magnétique extérieur ( E_H =0), E_m reste à minimiser :

$E_{m}=\mu _{0}/2\iiint H^{2}dv$ (SI) évalué sur toute la surface

avec H le champ magnétique, $\mu _{0}$ la perméabilité du vide et $dv$ un élément de volume.

Dans le cas :

a) où le matériau serait constitué d'un seul domaine magnétique les champs magnétiques générés seraient très grands et E_m serait maximum.

b) où le matériau contient deux domaines, E_m est divisé environ par deux et par quatre si le matériau est dans la configuration c).

Cependant il n'existe pas de matériau avec un nombre infini de domaines réduisant ainsi son énergie magnéto-statique à zéro. En effet, chaque domaine est séparé par une paroi qui a une énergie s'ajoutant à l'énergie totale du système. Le nombre de domaines est alors déterminé par un équilibre entre l'énergie des domaines et celle des parois de façon que l'énergie totale du système soit minimisée.

Énergie magnéto-statique par unité de surface d'un mono-domaine

L'énergie magnéto-statique d'un seul domaine magnétique dans un cristal mono-domaine est donnée par la formule suivante :

$E_{ms}=1/2N_{d}M_{s}^{2}$

où $N_{d}$ est le coefficient de démagnétisation du matériau et $M_{s}$ est l'aimantation du cristal constitué d'un seul domaine magnétique.

Pour un cube, dans une direction parallèle à un côté $N_{d}=1/3$ . Si l'on fait une approximation pour le schéma a), d'épaisseur L, on trouve une énergie magnétostatique sur le dessus du parallélépipède de :

$E_{ms}=1/6LM_{s}^{2}$ par unité de surface.

Énergie magnéto-statique par unité de surface d'un multi-domaine

L'énergie magnétostatique d'un domaine magnétique dans un cristal multi-domaine est donnée par la formule suivante :

$E_{ms}=0.85M_{s}^{2}D$

où D est l'épaisseur du domaine et $M_{s}$ est l'aimantation du cristal constitué de plusieurs domaines magnétiques.

Taille des domaines

Comme expliqué ci-dessus, à chaque fois qu'il y a plusieurs domaines, il a plusieurs parois. L'existence de parois a un coût énergétique, il faut donc que l'énergie dépensée par l'existence de la paroi ne soit pas supérieure à celle que l'on économise lors de la subdivision en domaines. Un matériau est dans son état d'équilibre quand son énergie totale est minimisée. Le nombre maximal de domaines correspond donc au nombre de domaines pouvant exister tant que l’énergie magnéto-statique économisée reste inférieure à l’énergie des parois de domaines en supposant que toutes les autres énergies soient minimisées.

L'énergie magnéto-statique par unité de surface associée est $E_{ms}=0.85M_{s}^{2}D$.

Il faut aussi considérer l'énergie par unité de surface d'une paroi à savoir : $E_{paroi}=\sigma {L \over D}$ avec $\sigma$ l'énergie par unité de surface, L la largeur totale et D la largeur du domaine.

$$E_{tot}=E_{ms}+E_{paroi}=0.85M_{s}^{2}D+\sigma {L \over D}$$

On cherche ensuite le minimum d'énergie lorsque ${dE \over dD}=0.85M_{s}^{2}-{\sigma L \over D^{2}}=0$

$D={\sqrt {\sigma L \over 0.85M_{s}^{2}}}$ et $E=2M_{s}{\sqrt {0.85\sigma L}}$

Dans la plupart des matériaux les domaines sont de taille microscopique, environ 10⁻⁴ à 10⁻⁶ m.

La structure des grains

Ce qui précède décrit la structure des domaines magnétiques dans un réseau cristallin parfait, comme c’est le cas pour le monocristal de fer. Toutefois la plupart des matériaux magnétiques sont polycristallins : composés de grains cristallins microscopiques. Les domaines ne sont pas identiques pour tous les grains. Chaque cristal a un axe de facile aimantation et est divisé en domaines avec l'axe d'aimantation qui lui est parallèle, selon des directions alternatives.

Photomicrographie de la surface d'un matériau ferromagnétique montrant les grains du cristal, chacun divisé en plusieurs domaines parallèles à l'axe "facile" d'aimantation.

Application d'un champ externe

Lors de l'application d'un champ magnétique externe l'énergie Zeeman s'ajoute à l’énergie totale et permet l'augmentation de la taille des domaines comme ci-dessous.

Augmentation de la taille des domaines magnétiques et leur orientation à la suite de l'application d'un champ magnétique extérieur.

Observation des domaines

Il existe de nombreuses techniques expérimentales pour mettre en évidence les domaines magnétiques ainsi que les parois qui les séparent. L'approche physique de l'observation des domaines est nettement différente suivant qu'il s'agit de matériaux ferromagnétiques, ferrimagnétiques ou antiferromagnétiques.

Domaines ferro- et ferrimagnétiques

La répartition d'aimantation agit directement sur différentes sondes : la lumière par les effets magnéto-optiques, les électrons par la force de Lorentz et les neutrons par le terme d'énergie potentielle d'interaction entre le champ et le moment magnétique du neutron, qui entraîne une contribution magnétique à la diffraction.

Observation d'une structure en domaine de Weiss par technique de Bitter

Méthode de Bitter

La méthode de Bitter, qui tient son nom du scientifique Francis Bitter, consiste à saupoudrer la surface polie du matériau magnétique à observer, d'une fine poudre ferromagnétique. Les hétérogénéités de l'aimantation présentes dans le matériau créent un champ dipolaire, dit champ de dispersion, qui attire ces fines particules magnétiques. Ces dernières se concentrent sur les parois magnétiques, permettant ainsi de déceler leur émergence à la surface de l'échantillon à l'aide d'un microscope optique, et de ce fait de révéler les domaines.

Observation par les effets magnéto-optiques

L'effet Faraday est utilisable pour observer les domaines, et cela grâce à une lumière polarisée rectilignement. Lorsque la lumière traverse l'échantillon, une rotation du plan de polarisation de cette dernière se produit. De plus, la polarisation de la lumière est proportionnelle à la projection de l'aimantation le long de la direction de propagation du faisceau, ainsi qu'à la longueur du projet parcouru. Pour deux domaines à 180°, c'est-à-dire dont l'aimantation est opposée, les sens de rotation de la polarisation sont opposés. L'effet Faraday n'est envisageable que pour des échantillons transparents. Un microscope polarisant de qualité moyenne suffit à observer la rotation de la polarisation.

Déplacement des domaines magnétiques dans un grain d'acier au silicium causé par l'application d'un champ magnétique externe croissant " vers le bas ", observé par un microscope Kerr. Les zones claires sont des domaines à aimantation "up", les zones sombres sont des domaines à aimantation "down".

Il est possible de suivre la réorganisation des domaines en temps réel en appliquant un champ magnétique.

Pour les échantillons métalliques non transparents, les observations sont tout de même possibles. Elles se font en réflexion en mettant en jeu l'effet Kerr magnéto-optique. Ce dernier permet de révéler les domaines lorsque l'aimantation possède une composante appréciable dans la direction perpendiculaire à la surface éclairée de l'échantillon.

L'effet Kerr longitudinal et l'effet Kerr transverse permettent de mettre en évidence les domaines lorsque les aimantations sont confinées dans le plan de la surface. Les rotations du plan de polarisation sont caractéristiques de l'effet longitudinal. Elles sont différentes suivant la composante dans le plan d'incidence de la direction de l'aimantation. L'effet transverse, se manifeste lui, par une différence d'intensité réfléchie suivant le signe de la composante de l'aimantation perpendiculaire au plan d'incidence.

L'observation par effet Kerr est plus difficile que par effet Faraday en raison de signaux plus faibles. Il exige une bonne instrumentation, c'est-à-dire un bon microscope polarisant ainsi qu'un excellent polissage de surface.

Observation par rayons X

L'imagerie par diffraction de Bragg des rayons X, souvent appelée topographie aux rayons X permet de faire l'image des défauts contenus dans un échantillon monocristallin ou dans des grains suffisamment grands. Son principe est que l'hétérogénéité du faisceau diffracté fournit une image de l'échantillon par le biais des déformations des plans réticulaires utilisés pour la réflexion de Bragg. Cette méthode révèle les domaines ou les parois entre les domaines, cependant leur visibilité est indirecte. En effet, le contraste est dû à l'effet secondaire que constitue la différence de distorsion, associé à la magnétostriction entre domaines. À l'intérieur d'un domaine, la magnétostriction tend à imposer une déformation spontanée qui dépend de la direction, mais non du sens de l'aimantation. La nécessité de raccorder le réseau cristallin entre deux domaines qui ont des directions d'aimantations différentes conduit généralement à une rotation relative du réseau dans les deux domaines.

Deux domaines à directions d'aimantation spontanée différentes sont alors dans des situations légèrement différentes vis-à-vis du faisceau incident et des conditions de Bragg. Si la divergence effective du faisceau est inférieur à leur différence d'orientation effective, les intensités diffractées par ces domaines sont différentes, ce qui conduit à des gris différents sur les régions correspondantes de l'image. Dans le cas contraire, quand l'écart angulaire entre les domaines est petit par rapport à la divergence effective du faisceau, les domaines ne se distinguent plus. Ce sont alors les parois que l'on observe, leurs images étant dues aux perturbations qu'elles imposent à la propagation des rayons X dans l'échantillon.

La topographie aux rayons X utilise des rayons X fournis par une source de rayonnement synchrotron. L'abondance des photons de haute énergie fournis par une machine telle que l'ESRF, la source européenne de rayonnement synchrotron, permet de voir des parois et domaines situés à l'intérieur d'un échantillon relativement épais. Les rayons X de rayonnement synchrotron sont exploités pour fournir des images par les effets de dichroïsme au voisinage de seuils d'absorption. Le dichroïsme désigne la variation d'absorption en fonction de l'état de polarisation du faisceau. Il est associé au fait que l'aimantation affecte profondément la répartition des états occupés et libres. Les photoélectrons sont émis, à la suite de domaines différents pour former l'image à l'aide d'une optique électronique. Cette observation, doit être fait sous ultra vide et ne concerne que le voisinage de la surface, à cause du faible parcours des photoélectrons.

Un microscope à rayons X mous utilise directement les rayons X transmis avec plus ou moins d'intensité selon l'absorption locale. Le caractère remarquable de cette technique est qu'elle concerne un élément chimique à la fois, celui dont on explore le seuil d'absorption. Elle donne donc des renseignements précieux sur le magnétisme des multicouches, et en particulier le couplage entre couches de compositions différentes.

Observation par les neutrons

Les neutrons interagissent avec la matière par deux mécanismes principaux. Ils subissent d'une part la diffusion nucléaire en raison de l'interaction forte avec les noyaux. D'autre part, ayant un moment magnétique associé à leur moment cinétique intrinsèque, ils ressentent le champ magnétique créé par les moments magnétiques atomiques à l'échelle microscopique. Ce mécanisme de diffusion magnétique des neutrons constitue la source de la plupart des informations dont on dispose sur les structures magnétiques.

Cette méthode peut fournir des images des domaines magnétiques de tous types à l'intérieur d'échantillons monocristallins massifs. À la différence des rayons X, l'information magnétique est directement associée à la définition des domaines et non à un effet secondaire. La technique la plus utile dans le cas des domaines ferro- ou ferrimagnétiques est basée sur les neutrons polarisés. Les contributions nucléaires et magnétiques à la diffraction s'ajoutent ou se retranchent suivant l'orientation relative de l'aimantation et de la polarisation des neutrons incidents. Pour une polarisation donnée du faisceau, il correspond un contraste entre domaines qui se renversent si on inverse la polarisation du faisceau. Sa résolution est médiocre (plusieurs dizaines de micromètres) en raison de la faible intensité des faisceaux disponibles.

Deux autres approches utilisent la précession de Larmor du moment magnétique des neutrons autour d'un champ magnétique moyen, ou d'une induction, pour cartographier des domaines. Un analyseur diffracte l'intensité et détecte une composante de polarisation du faisceau de neutrons transmis à travers l'échantillon. L'intensité varie selon la direction du champ magnétique ressenti donc de l'aimantation locale lorsque l'on déplace l'échantillon. Ce principe fournit des images de domaines grâce à un interféromètre neutronique.

L'interféromètre neutronique est constitué de trois ou quatre cristaux de silicium rigoureusement parallèles et parfaits, dans lequel le faisceau est divisé en deux de façon cohérente. Le faisceau est ensuite recombiné comme dans un interféromètre optique. Les cristaux de silicium opèrent la division, la déviation et la recombinaison des faisceaux par diffraction de Bragg.

Observation par les électrons

Les microscopies électroniques offrent des possibilités très riches d'observation de domaines ferromagnétiques. La technique la plus utilisée, et la plus directe, est la microscopie électronique en transmission (MET). Elle est basée sur le déphasage, ou en physique classique la force de Lorentz, qu'exerce le champ magnétique sur les électrons. Le renversement de l'aimantation entraîne l'inversion de la force de Lorentz, et donc une déviation en sens opposé du faisceau d'électrons. Les domaines ne sont pas observables dans l'image nette car les rayons issus d'un même point de l'objet convergent alors en un même point de l'image, quelle que soit leur déviation. Il faut donc défocaliser suffisamment le microscope pour pouvoir observer les domaines: les parois apparaissent sous forme de lignes sombres ou claires.

Observation par l'anisotropie d'une précipitation

D'après les travaux de Libovicky, il est possible d’observer à température ambiante les domaines existant vers 600 °C dans des échantillons de fer-silicium (10 à 15% atomique) grâce à l’anisotropie associée à la direction locale de l'aimantation et à la précipitation qui se produit lors d'un revenu. Le phénomène de ségrégation de phase métallurgique est sensible à la direction locale de l'aimantation. Cette technique ne se prête en aucun cas aux expériences en temps réel et est limitée à des matériaux aux diagrammes de phase complexes.

Domaines antiferromagnétiques

L’existence de domaines antiferromagnétiques ne conduit pas à l’abaissement de l’énergie libre d’un échantillon, contrairement au cas des domaines ferromagnétiques et ferrimagnétiques pour lesquels l’énergie dipolaire joue un rôle actif. Cependant, le passage de l’état paramagnétique à l’ordre antiferromagnétique étant associé à un abaissement de symétrie, plusieurs individus sont possibles. Ils se déduisent les uns des autres, géométriquement, par les éléments de symétrie perdus lors de la transition de phase. Leur étude est plus fondamentale que celle des ferro- ou ferrimagnétiques et très peu de travaux leur ont été consacrés.

Observation par microscopie optique

La visualisation des domaines antiferromagnétiques est quelquefois possible optiquement. L’oxyde de nickel, cubique au-dessus de sa température de Néel, comporte deux types de domaines :

• Domaines q ou domaines T (pour twin, nom donné à l’origine évoquant l’analogie avec les macles) : l’arrangement des moments magnétiques correspond à une alternance de plans dans lesquels les moments magnétiques sont alignés, le sens des moments étant inversé d’un plan au suivant. Cet ordre, qui correspond à une symétrie trigonale, caractérise quatre familles de domaines, suivant qu’il s’agit de l’une ou l’autre des quatre familles de plans {111}.
• Domaines S (pour spin) : l’orientation des moments magnétiques correspond à un abaissement supplémentaire de symétrie et donc à ces domaines.

Les biréfringences associées à ces distorsions permettent, en lumière polarisée, de voir les domaines. Il s’agit d’une visualisation indirecte dans la mesure où la distorsion est un effet secondaire de l’arrangement (striction d’échange) ou de l’orientation (magnétostriction) des moments magnétiques.

Observation par les rayons X et les électrons

La sensibilité de la diffraction de Bragg des rayons X à des distorsions cristallines permet à la topologie aux rayons X de déceler les domaines du type de ceux de NiO. Le mécanisme conduisant à leur visibilité est, comme dans le cas de la biréfringence optique de NiO, associé aux distorsions dues à l’arrangement et à l’orientation des moments magnétiques (striction d’échange et magnétostriction). La topographie aux rayons X présente généralement sur la lumière visible l’avantage d’une plus grande sensibilité à ces variations de distorsion, mais il s’agit également d’un effet indirect.

La microscopie électronique, moins sensible aux différences de distorsion, mais à résolution bien meilleure, a également permis des observations de domaines antiferromagnétiques basées sur les effets élastiques.

Observation par les neutrons

Le champ d’application le plus intéressant, sur le plan fondamental, de la topographie aux neutrons est probablement l’observation des domaines antiferromagnétiques. C’est en effet la seule technique qui les montre directement, par la contribution magnétique à la diffraction de Bragg. Dans le cas du NiO, l’arrangement des moments magnétiques des ions Ni²⁺  en feuillets à l’intérieur desquels ils sont parallèles conduit à une période spatiale doublée vis-à-vis de la sonde, sensible au sens des moments magnétiques, que constituent les neutrons. Des réflexions de Bragg purement magnétiques peuvent ainsi apparaître.

La topographie aux neutrons a également permis d’observer des domaines qu’aucune autre technique ne révèle. Dans le MnF₂ par exemple, les domaines à 180° peuvent être observés directement et en l’absence de champ magnétique, à l’aide de neutrons polarisés et d’une réflexion mixte (contributions nucléaires et magnétiques). La contribution nucléaire permet de distinguer les sommets et les centres de maille par la direction des voisins et la contribution magnétique permet de distinguer l’orientation des moments.

Sources

• L. Couture et R. Zitoun, Physique statistique, Ellipses, Paris, 1992
• Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], 1998 [détail des éditions]
• J.-P. Pérez, R. Carles et R. Fleckinger, Électromagnétisme. Fondements et applications, 3^e édition, Masson, coll. « Enseignement de la Physique », Paris, 1997
• Neil W. Ashcroft et N. David Mermin, Physique des solides [détail des éditions]
• Pierre HARTEMANN, Effets et matériaux magnétostrictifs, 1992, techniques de l'ingénieur.
• Sous la direction de Étienne du TREMOLET de LACHEISSERIE, Magnétisme, Tome I Collection Grenoble Sciences, janvier 1999