Fragilité (rhéologie)

En physique de la matière condensée, la fragilité d'un liquide vitrifiable caractérise la rapidité avec laquelle la dynamique du liquide ralentit lorsqu'il est refroidi vers la transition vitreuse : les liquides de grande fragilité se transforment en verre sur une plage de température relativement étroite, ceux de faible fragilité sur une plage relativement large. Physiquement, la fragilité peut être liée à la présence d'une hétérogénéité dynamique (en), et s'accompagne aussi d'une non validité de la relation de Stokes–Einstein entre viscosité et diffusion. Cette fragilité des liquides vitrifiables n'a pas de rapport direct avec la fragilité des matériaux solides.

Diagramme d'Angell (schématique), montrant la différence de comportement des liquides vitrifiables selon qu'ils sont « fragiles » ou « forts » (strong). η est la viscosité, T la température et T_g la température de transition vitreuse.

Définition

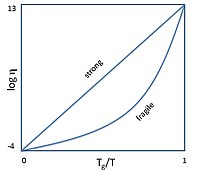
La fragilité reflète le degré auquel la dépendance à la température de la viscosité (ou du temps de relaxation) s'écarte du comportement d'Arrhenius. Cette classification a été initialement proposée par Austen Angell (en). La fragilité est caractérisée par l'« indice de fragilité cinétique » m, défini comme la dérivée (logarithmique) de la viscosité par rapport à la température à l'approche de la température de transition vitreuse (lors d'un refroidissement) :

$m=\left[{\frac {\partial \,\log _{10}\eta }{\partial \left(T_{\mathrm {g} }/T\right)}}\right]_{T=T_{\mathrm {g} }}={\frac {1}{\ln 10}}\left[{\frac {\partial \,\ln \eta }{\partial \left(T_{\mathrm {g} }/T\right)}}\right]_{T=T\mathrm {g} }=-{\frac {T_{\mathrm {g} }}{\ln 10}}\left({\frac {\partial \ln \eta }{\partial T}}\right)_{T=T\mathrm {g} }$

où η est la viscosité, T_g la température de transition vitreuse et T la température. Les liquides vitrifiables de grande fragilité sont dits « fragiles », ceux de faible fragilité sont dits « forts ». Par exemple la silice est « forte » tandis que certains polymères sont « fragiles ».

D'autres indices de fragilité ont été définis, notamment ceux de Bruning–- Sutton, d'Avramov et de Doremus :

• l'indice de fragilité de Bruning–Sutton, également noté m, repose sur la courbure ou la pente de la courbe représentant la viscosité en fonction de la température ;
• l'indice de fragilité d'Avramov, noté α (≥ 1), est fondé sur une formule de viscosité de type Kohlrausch dérivée pour les verres : un liquide vitrifiable est d'autant plus fragile que α est plus grand (α ≈ 1 pour les liquides forts) ;
• Doremus a remarqué que pratiquement tous les liquides suivent la loi d'Arrhenius à suffisamment basse ou haute température, mais avec des valeurs différentes pour l'énergie d'activation de la viscosité : une valeur élevée Q_H à basse température et une valeur faible Q_L à haute température (à température intermédiaire le comportement n'est plus arrhénien, l'énergie d'activation varie de Q_H à Q_L). L'indice de fragilité de Doremus est $R_{\mathrm {D} }=Q_{\mathrm {H} }/Q_{\mathrm {L} }$. Un liquide est d'autant plus fragile que R_D est plus élevé. Ses valeurs vont de 1,33 pour le dioxyde de germanium GeO₂ à 7,26 pour le diopside fondu CaMgSi₂O₆.

Aspects thermodynamiques et atomistiques

Le critère de fragilité de Doremus peut être exprimé en termes de paramètres thermodynamiques décrivant les défauts médiateurs de l'écoulement visqueux dans les oxydes fondus : $R_{\mathrm {D} }=1+{\frac {H_{\mathrm {d} }}{H_{\mathrm {m} }}}$, où $H_{\mathrm {d} }$ est l'enthalpie de formation et $H_{\mathrm {m} }$ l'enthalpie de mouvement de tels défauts. Par conséquent, la fragilité des oxydes fondus est un paramètre thermodynamique intrinsèque qui peut être déterminé sans ambiguïté par l'expérience.

La fragilité peut aussi s'exprimer analytiquement en fonction de paramètres physiques liés au potentiel d'interaction atomique ou moléculaire. Elle s'exprime notamment en fonction d'un paramètre qui mesure la raideur de la répulsion interatomique ou intermoléculaire, et du coefficient de dilatation thermique du liquide, lequel est au contraire lié à la partie attractive du potentiel d'interaction. L'analyse de différents systèmes (aussi bien des liquides de Lennard-Jones que des alliages métalliques) montre qu'une répulsion interatomique forte conduit à des liquides fragiles, et qu'inversement les atomes « mous » produisent des liquides forts.

Des expériences récentes de diffraction des rayons X par rayonnement synchrotron montrent un lien clair entre la fragilité du liquide et l'évolution structurale du liquide surfondu lors d'un refroidissement, par exemple l'intensification des pics Ni-P et Cu-P dans la fonction de distribution radiale près de la transition vitreuse.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fragility (glass physics) » (voir la liste des auteurs).