Graphe de Higman-Sims

Le graphe de Higman-Sims est, en théorie des graphes, un graphe 22-régulier possédant 100 sommets et 1100 arêtes.

Graphe de Higman-Sims
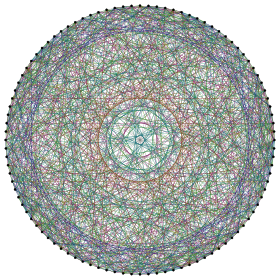Représentation du graphe de Higman-Sims
Nombre de sommets	100
Nombre d'arêtes	1100
Distribution des degrés	22-régulier
Rayon	2
Diamètre	2
Maille	4
Automorphismes	88 704 000
Propriétés	Fortement régulier Eulérien Hamiltonien

Propriétés

Propriétés générales

Le diamètre du graphe de Higman-Sims, l'excentricité maximale de ses sommets, est 2, son rayon, l'excentricité minimale de ses sommets, est 2 et sa maille, la longueur de son plus court cycle, est 4. Il s'agit d'un graphe 22-sommet-connexe et d'un graphe 22-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 22 sommets ou de 22 arêtes.

Propriétés algébriques

Le groupe d'automorphismes du graphe de Higman-Sims est un groupe d'ordre 88 704 000. Il est isomorphe au produit semi-direct du groupe de Higman-Sims d'ordre 44 352 000 avec le groupe cyclique d'ordre 2. Il agit transitivement sur l'ensemble des arêtes du graphe de Higman-Sims, faisant de lui un graphe arête-transitif, c'est-à-dire un graphe dont toutes les arêtes jouent exactement le même rôle.

Le polynôme caractéristique de la matrice d'adjacence du graphe de Higman-Sims est : $(x-22)(x-2)^{77}(x+8)^{22}$. Le graphe de Higman-Sims est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.

Voir aussi

Liens externes

(en) Eric W. Weisstein, « Higman-Sims Graph », sur MathWorld