Graphe de Nauru

En mathématiques, et plus précisément en théorie des graphes, le graphe de Nauru est un graphe 3-régulier possédant 24 sommets et 36 arêtes. Il a été nommé ainsi par David Eppstein d'après l'étoile à 12 branches ornant le drapeau de Nauru.

Graphe de Nauru
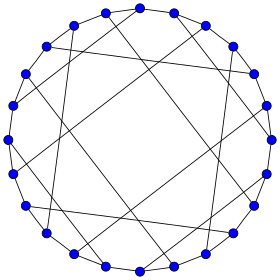Représentation du graphe de Nauru.
Notation	F24A
Nombre de sommets	24
Nombre d'arêtes	36
Distribution des degrés	3-régulier
Rayon	4
Diamètre	4
Maille	6
Automorphismes	144
Nombre chromatique	2
Indice chromatique	3
Propriétés	Régulier Biparti Cubique Intégral Hamiltonien Cayley

Propriétés

Propriétés générales

Le diamètre du graphe de Nauru, l'excentricité maximale de ses sommets, est 4, son rayon, l'excentricité minimale de ses sommets, est 4 et sa maille, la longueur de son plus court cycle, est 6. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.

Coloration

Le nombre chromatique du graphe de Nauru est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes. Ce nombre est minimal.

L'indice chromatique du graphe de Nauru est 3. Il existe donc une 3-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.

Propriétés algébriques

Le graphe de Nauru est symétrique, c'est-à-dire que son groupe d'automorphismes agit transitivement sur ses arêtes, ses sommets et ses arcs. Il est donc également arête-transitif et sommet-transitif. Le graphe de Nauru est l'unique graphe cubique symétrique à 24 sommets et sa notation dans le Foster Census, le catalogue classifiant tous les graphes cubiques symétriques, est F24A.

Le groupe d'automorphismes du graphe de Nauru est d'ordre 144. Sa structure exacte est connue : il est isomorphe au produit direct des groupes symétriques S₄ et S₃.

Le graphe de Petersen généralisé G(n,k) est sommet-transitif si et seulement si n = 10 et k =2 ou si k² ≡ ±1 (mod n). Il est arête-transitif seulement dans les sept cas qui suivent : (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), (24,5). Donc le graphe de Nauru est un des sept graphes de Petersen généralisés symétriques. Les six autres sont le graphe hexaédrique $G(4,1)$, le graphe de Petersen $G(5,2)$, le graphe de Möbius-Kantor $G(8,3)$, le graphe dodécaédrique $G(10,2)$ et le graphe de Desargues $G(10,3)$.

Le polynôme caractéristique de la matrice d'adjacence du graphe de Nauru est : $(x-3)(x-2)^{6}(x-1)^{3}x^{4}(x+1)^{3}(x+2)^{6}(x+3)$. Il n'admet que des racines entières. Le graphe de Nauru est donc un graphe intégral, un graphe dont le spectre est constitué d'entiers.

Propriétés topologiques

Le plongement symétrique du graphe de Nauru dans un tore, formé en collant ensemble les arêtes opposées de l'hexagone régulier externe

Un plongement symétrique du graphe de Nauru sur une surface de genre 4, ayant six faces dodécagonales.

Le graphe de Nauru possède deux plongements distincts qu'on peut considérer comme des polyèdres réguliers généralisés : des surfaces (ou plus précisément des variétés de dimension 2) décomposées en sommets, arêtes et faces de telle sorte qu'il y ait une bijection (respectant les relations d'incidence) de la surface envoyant n'importe quel drapeau (un triplet formé d'un sommet, d'une arête et d'une face incidents) vers n'importe quel autre drapeau.

Un de ces deux plongements forme un tore et le graphe de Nauru est donc un graphe toroïdal : il est formé de 12 faces hexagonales, et des 24 sommets et 36 arêtes du graphe de Nauru. Le graphe dual de ce plongement est un graphe symétrique 6-régulier à 12 sommets et 36 arêtes.

L'autre plongement symétrique du graphe de Nauru a six faces dodécagonales, et forme une surface de genre 4. Son dual n'est pas un graphe simple, mais un multigraphe, puisque chaque face a trois côtés communs avec quatre autres faces. Ce graphe dual peut être construit à partir d'un octaèdre régulier en en remplaçant chaque arête par un faisceau de trois arêtes "parallèles".

L'ensemble des faces de chacun de ces deux plongements est l'ensemble des polygones de Pétrie de l'autre plongement.

Histoire

Le drapeau de Nauru.

La première personne à publier sur le graphe de Nauru est R. M. Foster dans un effort pour recenser tous les graphes cubiques symétriques. La liste complète des graphes cubiques symétriques a été nommée Foster Census d'après lui, dans cette liste le graphe de Nauru porte le numéro F24A mais n'a pas de nom spécifique. En 1950, H. S. M. Coxeter cite le graphe une seconde fois, donnant la représentation hamiltonienne utilisée pour illustrer cet article et le décrivant comme le graphe de Levi de la configuration projective découverte par Zacharias.

En 2003, Ed Pegg indique dans la publication internet de la Mathematical Association of America que le F24A mérite un nom mais n'en propose aucun. Finalement, en 2007, David Eppstein la nomme Nauru graph en référence au drapeau de Nauru qui contient une étoile à douze branches similaire à celle qui apparait dans la construction du graphe comme un graphe de Petersen généralisé.

Voir aussi

Articles connexes

• Théorie des graphes