Graphomètre
Le graphomètre est un ancien instrument de mesure angulaire. Monté sur rotule, il permet de relever des angles entre objets situés dans un même plan. C'est un instrument de géodésie et de topographie.

Il a été inventé par Philippe Danfrie, l'aîné plutôt que le jeune, en 1597, si on en croit les lettres patentes faites par Henri IV en 1606 et son testament[1]. Ce demi-cercle comportant alidades et pinnules sera très employé pendant plus de 150 ans. Lui succèdera le graphomètre à lunettes, vers les années 1760[2].
Le graphomètre à pinnules
modifierDescription
modifier
D'après la figure ci-contre (instrument de 1889).
Le graphomètre à pinnules est constitué d'un demi-cercle fixe : son diamètre mesure de 20 à 40 cm environ, et son limbe est gradué en degrés. Sur ce demi-cercle est centrée une alidade fixe (FH). Une autre alidade à pinnules (DE) est mobile autour de l'axe central. Une position angulaire (R) de cette dernière est repérée sur les graduations du limbe et peut être mesurée précisément grâce à un vernier. Au centre se trouve une boussole pour l'orientation éventuelle. Le tout est accroché à un support à rotule qui permet l'inclinaison.
Mise en œuvre
modifierPour effectuer une mesure, il faut procéder de la façon suivante :
- fixer le centre C du graphomètre à pinnules à la verticale d’un point de station ;
- mettre l'instrument dans le plan, le plus souvent horizontal[N 1], des objets à viser, grâce au support à rotule (G) ;
- régler les alidades en fonction des objets : une des alidades est utilisée pour viser l’objet , tandis que l’autre (et son vernier) est utilisée pour viser l’objet ;
- lire, par l'intermédiaire du vernier, l'angle entre les deux objets.
Utilisation
modifier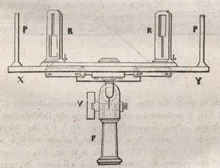
Le graphomètre est utilisé dans différentes applications, mais, au XVIIe siècle, le calcul trigonométrique est inconnu des géomètres-topographes, Danfrie propose une méthode originale pour exploiter les résultats des mesures. Le principe de la méthode est le suivant :
- l'opérateur, sur le terrain, mesure une base puis prend ses angles ;
- il reporte ensuite sur plan ses figures géométriques à la règle rapporteur ;
- pour terminer, il calcule, par la méthode des triangles semblables, les différents éléments qu'il veut connaitre, à partir des valeurs linéaires ou angulaires relevées sur plan.
Danfrie détaille diverses applications mettant en œuvre son graphomètre et sa méthode :
- mesure de hauteur : le graphomètre (vertical) est en O, on a FG/KL = FO/KI, d'où la hauteur FG = FO.KL/KI ;
- mesure de distance : suivant le même principe on peut calculer les distances des opérateurs au point levé ;
- triangulation simple : la méthode reste la même. Remarque : la base mesurée doit être la plus grande possible - pour plus d'exactitude - ici ce sera AB ;
- levé de plans : c'est la généralisation de la méthode.
-
Mesure de hauteur.
-
Mesure de distance.
-
Triangulation simple.
-
Levé de plan.
On voit que la base ne mesure que quelques toises ; les angles mesurés au graphomètre sont obtenus au degré près. Les résultats ne seront guère exacts. L'instrument sera amélioré par l'adjonction de lunettes.
Le graphomètre à deux lunettes
modifierLes deux alidades sont remplacées par des lunettes de visée avec réticule. Le limbe peut être divisé par transversales. Les résultats de mesures sont plus exacts ; ils sont exploités par le calcul (trigonométrie et logarithmes).
-
Graphomètre à deux lunettes, Bion, 1709.
Ce dernier type d'instrument est employé par les ingénieurs de Cassini III pour effectuer des levés de triangulations secondaires. Ces relevés d'angles ont servi à l'établissement de la carte de France des Cassini[3].
Notes et références
modifierNotes
modifier- En topographie, les angles sont réduits dans le plan horizontal. L'horizontalité de l'instrument, en 1889, est obtenue grâce à un niveau à bulle.
Références
modifier- Philippe Danfrie, Declaration de l'usage du graphometre, par la pratigue…, Paris, Chez l'auteur, (lire en ligne).
- Maurice Daumas, Les instruments scientifiques aux XVIIe siècle et XVIIIe siècle, Paris, P.U.F., , p. 24, 25.
- Monique Pelletier, Les cartes des Cassini, (ISBN 2-7355-0525-1), p. 124.








