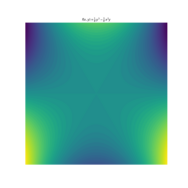Isomorphisme de Harish-Chandra

En mathématiques, l'isomorphisme de Harish-Chandra, défini par Harish-Chandra en 1951, est un isomorphisme d'anneaux commutatifs entre le centre ${\mathcal {Z}}(U({\mathfrak {g}}))$ de l'algèbre enveloppante universelle $U({\mathfrak {g}})$ d'une algèbre de Lie réductive ${\mathfrak {g}}$ et les éléments $S({\mathfrak {h}})^{W}$ de l'algèbre symétrique $S({\mathfrak {h}})$ d'une sous-algèbre de Cartan ${\mathfrak {h}}$ invariants sous l'action du groupe de Weyl $W$ .

Introduction

Soient ${\mathfrak {g}}$ une algèbre de Lie semi-simple, ${\mathfrak {h}}$ sa sous-algèbre de Cartan et $\lambda ,\mu \in {\mathfrak {h}}^{*}$ deux éléments de l'espace de poids (où ${\mathfrak {h}}^{*}$ est le dual de ${\mathfrak {h}}$ ). On fixe qu’un ensemble de racines positives $\Phi _{+}$ . Soient $V_{\lambda }$ et $V_{\mu }$ les modules de poids correspondant à $\lambda$ et $\mu$ respectivement.

Caractères centraux

Les ${\mathfrak {g}}$ -modules $V_{\lambda }$ et $V_{\mu }$ sont des représentations de l'algèbre enveloppante universelle $U({\mathfrak {g}})$ et son centre agit sur les modules par multiplication scalaire (cela découle du fait que les modules sont générés par un vecteur de poids le plus élevé). Donc pour $v\in V_{\lambda }$ et $x\in {\mathcal {Z}}(U({\mathfrak {g}}))$ , $x\cdot v:=\chi _{\lambda }(x)v$ et de même pour $V_{\mu }$ . Les fonctions $\chi _{\lambda },\,\chi _{\mu }$ sont des caractères de ${\mathcal {Z}}(U({\mathfrak {g}}))$ dits caractères centraux.

Énoncé du théorème de Harish-Chandra

Pour tous $\lambda ,\mu \in {\mathfrak {h}}^{*}$ , il y a égalité des caractères $\chi _{\lambda }=\chi _{\mu }$ si et seulement si $\lambda +\delta$ et $\mu +\delta$ sont dans la même orbite du groupe de Weyl ${\mathfrak {h}}^{*}$ , où $\delta$ est la demi-somme des racines positives, parfois appelée vecteur de Weyl^[1].

Isomorphisme explicite

Plus explicitement, l'isomorphisme peut être construit comme la composition de deux applications, l'une de ${\mathfrak {Z}}={\mathcal {Z}}(U({\mathfrak {g}}))$ à $U({\mathfrak {h}})=S({\mathfrak {h}}),$ et un autre de $S({\mathfrak {h}})$ dans lui-même.

La première est une projection $\gamma :{\mathfrak {Z}}\rightarrow S({\mathfrak {h}})$ . Pour un choix de racines positives $\Phi _{+}$ , on définit $n^{+}=\bigoplus _{\alpha \in \Phi _{+}}{\mathfrak {g}}_{\alpha },n^{-}=\bigoplus _{\alpha \in \Phi _{-}}{\mathfrak {g}}_{\alpha }$ les sous-algèbre nilpotente positive et sous-algèbre nilpotente négative respectivement, en raison du théorème de Poincaré – Birkhoff – Witt, il y a une décomposition $U({\mathfrak {g}})=U({\mathfrak {h}})\oplus (U({\mathfrak {g}}){\mathfrak {n}}^{+}+{\mathfrak {n}}^{-}U({\mathfrak {g}})).$ Si $z\in {\mathfrak {Z}}$ est central, alors en fait $z\in U({\mathfrak {h}})\oplus (U({\mathfrak {g}}){\mathfrak {n}}^{+}\cap {\mathfrak {n}}^{-}U({\mathfrak {g}})).$ La restriction de la projection $U({\mathfrak {g}})\rightarrow U({\mathfrak {h}})$ au centre est $\gamma :{\mathfrak {Z}}\rightarrow S({\mathfrak {h}})$ , et est un homomorphisme des algèbres. Ceci est lié aux caractères centraux par $\chi _{\lambda }(x)=\gamma (x)(\lambda )$ La deuxième application est l'application de torsion $\tau :S({\mathfrak {h}})\rightarrow S({\mathfrak {h}})$ définie sur ${\mathfrak {h}}$ par $\tau (h)=h-\delta (h)1$ avec $\delta$ le vecteur de Weyl.

Alors ${\tilde {\gamma }}=\tau \circ \gamma :{\mathfrak {Z}}\rightarrow S({\mathfrak {h}})$ est l'isomorphisme d'Harish-Chandra. La raison pour laquelle la torsion est introduite est que $\chi _{\lambda }$ n'est pas réellement invariant de Weyl, mais on peut prouver que le caractère tordu ${\tilde {\chi }}_{\lambda }=\chi _{\lambda -\delta }$ l'est.

Applications

Le théorème a été utilisé pour obtenir une preuve algébrique de la formule des caractères de Weyl pour les représentations irréductibles de dimension finie^[2]. La preuve a été encore simplifiée par Victor Kac, de sorte que seul l'opérateur de Casimir est nécessaire.

Une conséquence simple est que pour les modules de Verma ou les modules Verma généralisés $V_{\lambda }$ de poids $\lambda$ , il n’existe qu’un nombre fini de poids $\mu$ pour lequel un morphisme non nul $V_{\lambda }\rightarrow V_{\mu }$ existe.

Invariants fondamentaux

Pour ${\mathfrak {g}}$ une algèbre de Lie simple, soit $r$ soit son rang, c'est-à-dire la dimension de toute sous-algèbre de Cartan ${\mathfrak {h}}$ de ${\mathfrak {g}}$ . H. S. M. Coxeter a observé que $S({\mathfrak {h}})^{W}$ est isomorphe à une algèbre de polynômes en $r$ variables (voir le théorème de Chevalley-Shephard-Todd pour un énoncé plus général). Par conséquent, le centre de l'algèbre enveloppante universelle d'une algèbre de Lie simple est isomorphe à une algèbre de polynômes. Les degrés des générateurs de l'algèbre sont les degrés des invariants fondamentaux donnés dans le tableau suivant.

Algèbre de Lie	Nombre de Coxeter h	Nombre de Coxeter dual	Degré des invariants fondamentaux
R	0	0	1
A_n	n + 1	n + 1	2, 3, 4,... , n + 1
B_n	2n	2n − 1	2, 4, 6, ... , 2n
C_n	2n	n + 1	2, 4, 6, ... , 2n
D_n	2n − 2	2n − 2	n ; 2, 4, 6, ... , 2n − 2
E₆	12	12	2, 5, 6, 8, 9, 12
E₇	18	18	2, 6, 8, 10, 12, 14, 18
E₈	30	30	2, 8, 12, 14, 18, 20, 24, 30
F₄	12	9	2, 6, 8, 12
G₂	6	4	2, 6

Le nombre d’invariants fondamentaux d’un groupe de Lie est égal à son rang. Les invariants fondamentaux sont également liés à l'anneau de cohomologie d'un groupe de Lie. En particulier, si les invariants fondamentaux ont des degrés $d_{1},\cdots ,d_{r}$ , alors les générateurs de l'anneau de cohomologie ont des degrés $2d_{1}-1,\cdots ,2d_{r}-1$ . De ce fait, les degrés des invariants fondamentaux peuvent être calculés à partir des nombres de Betti du groupe de Lie et vice versa. Dans une autre direction, les invariants fondamentaux sont liés à la cohomologie de l'espace de classification. L'anneau de cohomologie $H^{*}(BG,\mathbb {R} )$ est isomorphe à une algèbre polynomiale sur des générateurs à degrés $2d_{1},\cdots ,2d_{r}$ ^[3].

Exemples

Si ${\mathfrak {g}}$ est l'algèbre de Lie ${\mathfrak {sl}}(2,\mathbb {R} )$ , alors le centre de l'algèbre enveloppante universelle est généré par l'invariant de Casimir de degré 2, et le groupe de Weyl agit sur la sous-algèbre de Cartan, qui est isomorphe à $\mathbb {R}$ . Donc l'invariant du groupe de Weyl est le carré du générateur de la sous-algèbre de Cartan, qui est également de degré 2.
Pour ${\mathfrak {g}}=A_{2}={\mathfrak {sl}}(3,\mathbb {C} )$ , l'isomorphisme de Harish-Chandra dit que ${\mathcal {Z}}(U({\mathfrak {g}}))$ est isomorphe à une algèbre polynomiale de polynômes invariants de Weyl à deux variables $h_{1},h_{2}$ (puisque la sous-algèbre de Cartan est deux dimensionnel). Pour $A_{2}$ , le groupe de Weyl est $S_{3}\cong D_{6}$ qui agit sur la sous-algèbre de Cartan. Le groupe de Weyl agit par réflexions, ce sont donc des isométries et donc le polynôme de degré 2 $f_{2}(h_{1},h_{2})=h_{1}^{2}+h_{2}^{2}$ est un invariant de Weyl. Une ébauche du polynôme invariant de Weyl de degré 3 (pour un choix particulier de représentation standard où l'une des réflexions se trouve sur l'axe des x) est présentée ci-dessous. Ces deux polynômes génèrent l'algèbre polynomiale et sont les invariants fondamentaux de $A_{2}$ .
Pour toutes les algèbres de Lie de la classification, il existe un invariant fondamental de degré 2, l'opérateur de Casimir. À travers l'isomorphisme, celui-ci correspondent à un polynôme de degré 2 sur la sous-algèbre de Cartan. Le polynôme invariant est $f_{2}(\mathbf {h} )=h_{1}^{2}+\cdots +h_{r}^{2}$ où r est la dimension de ${\mathfrak {h}}$ , le rang de l'algèbre de Lie.
Pour ${\mathfrak {g}}=A_{1}={\mathfrak {sl}}(2,\mathbb {C} )$ , la sous-algèbre de Cartan est unidimensionnelle, et l'isomorphisme de Harish-Chandra montre que ${\mathcal {Z}}(U({\mathfrak {g}}))$ est isomorphe à l'algèbre des polynômes invariants de Weyl en une seule variable $h$ . Le groupe de Weyl est $S_{2}$ agissant par réflexion, avec un élément non trivial agissant sur les polynômes par $h\mapsto -h$ . La sous-algèbre des polynômes invariants de Weyl dans l'algèbre polynomiale complète $K[h]$ est constituée des polynômes pairs, générés par $f_{2}(h)=h^{2}$ .

L'invariant fondamental de degré 3 pour A₂.

Généralisation aux algèbres de Lie affines

Le résultat ci-dessus est valable pour les algèbres de Lie réductives, et en particulier semi-simples. Il existe une généralisation aux algèbres de Lie affines montrée par Feigin et Frenkel montrant qu'une algèbre connue sous le nom de centre Feigin-Frenkel est isomorphe à une algèbre W associée à l'algèbre de Lie duale de Langlands $^{L}{\mathfrak {g}}$ ^[4] ^,^[5].

Notes

↑ Humphreys 1978, p. 130.
↑ Humphreys 1978, p. 135–141.
↑ Borel, « Sur la cohomologie des espaces homogenes des groupes de Lie compacts », American Journal of Mathematics, vol. 76, n^o 2,‎ avril 1954, p. 273–342
↑ Molev, « On Segal–Sugawara vectors and Casimir elements for classical Lie algebras », Letters in Mathematical Physics, vol. 111, n^o 8,‎ 19 janvier 2021 (DOI 10.1007/s11005-020-01344-3, arXiv 2008.05256, S2CID 254795180)
↑ Feigin, Frenkel et Reshetikhin, « Gaudin Model, Bethe Ansatz and Critical Level », Commun. Math. Phys., vol. 166,‎ 3 avril 1994, p. 27–62 (DOI 10.1007/BF02099300, arXiv hep-th/9402022, S2CID 17099900)

Lien externe

(en) Brian Weber, « Notes on the Harish-Chandra isomorphism », sur université de Pennsylvanie

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Harish-Chandra isomorphism » (voir la liste des auteurs).
Harish-Chandra, « On some applications of the universal enveloping algebra of a semisimple Lie algebra », Transactions of the American Mathematical Society, vol. 70, n^o 1,‎ 1951, p. 28-96 (DOI 10.2307/1990524 , JSTOR 1990524, MR 0044515)
James E. Humphreys, Introduction to Lie algebras and representation theory, vol. 9, Springer-Verlag, coll. « Graduate Texts in Mathematics », 1978 (ISBN 0-387-90053-5, MR 0499562) (Contains an improved proof of Weyl's character formula.)
James E. Humphreys, Representations of semisimple Lie algebras in the BGG category O, AMS, 2008 (ISBN 978-0-8218-4678-0), p. 26
Anthony W. Knapp et David A. Vogan, Cohomological induction and unitary representations, vol. 45, Princeton University Press, coll. « Princeton Mathematical Series », 1995 (ISBN 978-0-691-03756-1, MR 1330919)
Anthony W. Knapp, « V. Finite Dimensional Representations §5. Harish-Chandra Isomorphism », dans Lie Groups Beyond an Introduction, vol. 140, Springer, coll. « Progress in Mathematics », 2013 (1^re éd. 1996), 246-258 p. (ISBN 978-1-4757-2453-0, lire en ligne)

Portail des mathématiques

[Humphreys1978130-1] Humphreys 1978, p. 130.

[Humphreys1978135–141-2] Humphreys 1978, p. 135–141.

[borel_sur_la_cohomologie-3] Borel, « Sur la cohomologie des espaces homogenes des groupes de Lie compacts », American Journal of Mathematics, vol. 76, n^o 2,‎ avril 1954, p. 273–342

[molev-4] Molev, « On Segal–Sugawara vectors and Casimir elements for classical Lie algebras », Letters in Mathematical Physics, vol. 111, n^o 8,‎ 19 janvier 2021 (DOI 10.1007/s11005-020-01344-3, arXiv 2008.05256, S2CID 254795180)

[ffr-5] Feigin, Frenkel et Reshetikhin, « Gaudin Model, Bethe Ansatz and Critical Level », Commun. Math. Phys., vol. 166,‎ 3 avril 1994, p. 27–62 (DOI 10.1007/BF02099300, arXiv hep-th/9402022, S2CID 17099900)

[1]

[2]

[3]

[4]

[5]