Mesurage (métrologie)

En métrologie, une mesure ou un mesurage, est le « processus consistant à obtenir expérimentalement une ou plusieurs valeurs que l'on peut raisonnablement attribuer à une grandeur ».

Mesurage avec une colonne de mesure.

C'est la définition donnée par le Bureau international des poids et mesures dans un document largement diffusé définissant la terminologie de la métrologie, le Vocabulaire international de métrologie.

Il est à remarquer que :

• les mesurages ne s'appliquent qu'aux propriétés quantitatives ; sont donc exclues les propriétés qualitatives ;
• tout mesurage implique la comparaison de grandeurs et comprend le comptage d'entités ;
• en métrologie, un mesurage se traduit finalement par un résultat de mesure, en employant un système (ou instrument) de mesure étalonné, et suivant une procédure de mesure.

Les mesures sont susceptibles d'erreurs et d'incertitudes ; aussi, en fonction de leur aptitude à donner des résultats corrects, elles peuvent être qualifiées de différentes façons.

Terminologie

La définition d'un mesurage s'appuie sur des termes précisés ou non du VIM ; suivent d'autres termes employés dans la page et précisés par le VIM.

Processus de mesure

Le « processus de mesure » met en œuvre un certain nombre d'éléments que l'on peut présenter ici succinctement par l'approche 5 M, soit :

1. La matière, ici le mesurande ou la grandeur à mesurer ;
2. Le matériel ou instrument de mesure ;
3. La méthode : procédure de mesure ;
4. La main-d'œuvre, c'est-à-dire, l'opérateur ;
5. Le milieu, soit l'influence de l'environnement - la température notamment - sur le mesurage.

Valeur d'une grandeur

La « valeur d'une grandeur » soit, d'après le VIM : « ensemble d'un nombre et d'une référence constituant l'expression quantitative d'une grandeur ». C'est généralement le produit d'un nombre et d'une unité de mesure. Exemples : la longueur d'une tige métallique : 24,97 cm ou 249,7 mm ; la masse d'une personne : 64 kg ; la vitesse d'une automobile : 96 km/h ; la température Celsius d'un compartiment de congélateur : −20 °C…

Mesurande

Le « mesurande » est la grandeur que l'on veut mesurer. Soit par exemple la longueur d'une tige à mesurer qui peut être connue ou inconnue : ce peut être une tige étalon connue de 100 mm de valeur vraie (à la température de référence 20 °C) ou une tige fabriquée - inconnue, que l'on va mesurer - suivant la spécification de 100 ± 0,15 mm.

Valeur vraie

La « valeur vraie » d'une grandeur de référence est « sa valeur considérée comme unique et, en pratique, impossible à connaître ». C'est le cas des étalons dont l'incertitude est négligeable par rapport à l'incertitude de mesure du mesurande. Exemple : la tige étalon de 100 mm citée, dite de classe 3, a une tolérance de ± 2,5 μm et une incertitude de ± 1,25 μm ; cette tige va servir à étalonner l'instrument de mesure employé pour mesurer les tiges fabriquées suivant la cote de 100 ± 0,15 mm. La tolérance de la spécification (± 0,15 mm) est très grande par rapport à la tolérance (± 2,5 μm) et l'incertitude (± 1,25 μm) de l'étalon. On peut donc considérer que sa valeur vraie (d'ailleurs gravée sur l'étalon) est de 100 mm.

Incertitude de mesure

L'« incertitude de mesure » est, sommairement, « la dispersion des valeurs attribuées à un mesurande, à partir des informations utilisées ». Exemple : après étalonnage sur l'étalon de 100 mm, l'instrument à une incertitude globale supposée de ± 0,03 mm.

Résultat de mesure

Un « résultat de mesure » est un « ensemble de valeurs attribuées à un mesurande, complété par toute autre information pertinente disponible … Le résultat de mesure est généralement exprimé par une valeur mesurée unique et une incertitude de mesure. Si l'on considère l'incertitude de mesure comme négligeable dans un certain but, le résultat de mesure peut être exprimé par une seule valeur mesurée. Dans de nombreux domaines, c'est la manière la plus usuelle d'exprimer un résultat de mesure ».

Exemples simplifiés :

• Un premier mesurage d'une pièce particulière fabriquée suivant la spécification 100 ± 0,15 mm, comme cité précédemment, a donné la valeur 99,7 mm. Le résultat de cette mesure unique peut s'exprimer ainsi :

Valeur : 99,7 mm avec une incertitude globale associée de ± 0,03 mm, soit V = 99,7 mm ± 0,03 mm.

• Un autre mesurage indépendant du précédent, de cinq valeurs consécutives, donne les valeurs suivantes : 99,7 ; 99,72 ; 99,69 ; 99,73 ; 99,69 mm. Le résultat de mesure peut s'exprimer de la façon suivante :

Valeur moyenne : 99,706 mm ; incertitude globale associée ± 0,017 mm, soit V_m = 99,706 mm ± 0,017 mm.

Remarques :

• le résultat final, en ne gardant que deux chiffres significatifs après la virgule s'exprimerait plutôt par : V_m = 99,7 mm ± 0,02 mm.
• l'incertitude sur la moyenne de cinq valeurs est réduite par rapport à l'incertitude sur une seule valeur, ce qui est logique. La démonstration de cette réduction dépasse le cadre de cette présentation.

L'expression du résultat d'un mesurage, avec une incertitude associée, concerne les laboratoires et le domaine industriel travaillant avec des partenaires dans un rapport « client-fournisseur ». Pour des mesurages non contractuels industriels et dans le domaine « grand public » on se contente le plus souvent d'une seule valeur lue comme résultat de mesurage.

Erreur et incertitude de mesure

Erreur de mesure : « différence entre une valeur mesurée et une valeur de référence ». Cette notion d'erreur est trop complexe pour être développée ici.

L'incertitude de mesure : est « la dispersion des valeurs attribuées à un mesurande » présentée plus haut. Un article détaillé développe le sujet.

Qualification des mesures

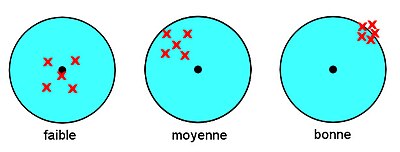
Pour comparer des mesurages d'une même référence par différents processus de mesure on peut être amené à employer des termes qualifiant de façons différentes ces comparaisons. Ces termes sont l'exactitude, la justesse et la fidélité de mesure.

Exactitude de mesure

« étroitesse de l'accord entre une « valeur mesurée » et une valeur vraie d'un mesurande. »

Remarques : Ce n'est pas une grandeur et elle ne s'exprime pas numériquement. Elle peut servir à classer différentes mesures. Elle remplace l'ancien terme « précision » qui n'est plus à employer en métrologie.

Exemple simple : deux mesurages différents de l'étalon de 100 mm précisé plus haut ont donné respectivement : 99,999 mm et 100,003 mm. On peut dire que l'exactitude de la première mesure est meilleure que la seconde, ceci quel que soit le processus de mesure et son incertitude.

Exactitude de mesure (distance OX).

Justesse de mesure

« Étroitesse de l'accord entre la « moyenne » d'un nombre infini de valeurs mesurées répétées et une valeur de référence. »

Remarque : Comme l'exactitude, ce n'est pas une grandeur et elle ne s'exprime pas numériquement.

Exemple simple : deux mesurages d'une cinquantaine de valeurs différentes de l'étalon de 100 mm précisé plus haut ont donné respectivement comme valeur moyenne : 100,002 mm et 99,997 mm. On peut dire que la justesse du premier mesurage est meilleure que celle du second, ceci quel que soit le processus de mesure et son incertitude.

Justesse de mesure (distance Oo).

Fidélité de mesure

« étroitesse de l'accord entre les indications ou les valeurs mesurées obtenues par des mesurages répétés du même objet ou d'objets similaires dans des conditions spécifiées. »

Remarque : À la différence de l'exactitude et de la justesse, la fidélité s'exprime numériquement. Elle peut être exprimée par l'écart-type de la dispersion des mesures considérées.

Exemple simple : Un mesurage de cinq valeurs consécutives d'une pièce particulière fabriquée suivant la spécification 100 ± 0,15 mm, comme cité précédemment, donne les valeurs suivantes : 99,7 ; 99,72 ; 99,69 ; 99,73 ; 99,69 mm. L'écart-type expérimental de la dispersion sur ces valeurs est σ _n-1 < 0,02 (en vrai : 0,01816…) ; c'est la fidélité de mesure de l'expérience.

Fidélité de mesure (Ø enveloppe des X).

Notes et références

Annexes

Bibliographie

Jean Perdijon, Pour faire bonne mesure, Les Ulis, EDP sciences, 2020.

 : document utilisé comme source pour la rédaction de cet article.

• (en + fr) VIM collectif, JCGM 200 : 2008 : Vocabulaire international de métrologie - Concepts fondamentaux et généraux et termes associés, BIPM, 2008 (lire en ligne)
• Collectif AFNOR, Métrologie dans l'entreprise : Outil de la qualité, Paris, AFNOR, 1996, 310 p. (ISBN 2-12-460701-4)
• Collectif CNDP, La mesure : Actes des 7^es entretiens de la Villette, Paris, CNDP, 1995, 381 p. (ISBN 2-240-00409-6) (ISBN sur l'ouvrage erroné)
• M. Collinet CNAM, Expression des incertitudes de mesures, Senlis, CETIM, 1995

Articles connexes

Métrologie ; Mesure (épistémologie) ; Étalonnage (métrologie) ; Erreur (métrologie) ; Calcul d'incertitude ; Dispersion statistique ; Instrument de mesure…

Liens externes

• Vocabulaire international de métrologie — Concepts fondamentaux et généraux et termes associés (VIM)