Loi de Morrie

La loi de Morrie est l'identité trigonométrique suivante :

Richard Feynman en 1984, quelques années avant sa mort. Il se souvenait encore de cette curiosité apprise pendant l'enfance.

$\cos(20^{\circ })\cdot \cos(40^{\circ })\cdot \cos(80^{\circ })={\frac {1}{8}}$.

Le nom de cette « curiosité » est dû au physicien Richard Feynman, qui la tient d'un ami d'enfance, Morrie Jacobs.

Cette identité est intrigante parce qu'aucun des facteurs du produit n'est rationnel, mais que le produit l'est.

Histoire

Dans son enfance, Richard Feynman avait l'habitude d'échanger des anecdotes mathématiques avec ses amis. C'est l'un d'eux, nommé Morrie Jacobs, qui lui a fait connaître cette égalité. Il s'en est ensuite souvenu toute sa vie, de même que les circonstances dans lesquelles il en a appris l'existence (dans le magasin de cuir du père de Morrie). Il y fait référence dans une lettre à Morrie datée du 27 janvier 1987.

Après la mort de Feynman en 1988, James Gleick raconte cet épisode en 1992 dans Genius, la biographie qu'il a écrite du physicien.

En 1996, Beyer et al. appellent cette égalité « Morrie Jacobs's identity » (litt. « identité de Morrie Jacobs »). En 1998, Anderson l'appelle « Morrie's Law » (litt. « loi de Morrie »). En 2011, Nahin l'appelle « Jacobs-Feynman equality » (litt. « égalité de Jacobs-Feynman »).

Identités similaires

En radians, la loi de Morrie s'exprime ainsi :

$\cos \left({\frac {\pi }{9}}\right)\cdot \cos \left({\frac {2\pi }{9}}\right)\cdot \cos \left({\frac {4\pi }{9}}\right)={\frac {1}{8}}$.

Elle utilise la fonction cosinus, mais des identités similaires existent pour d'autres fonctions trigonométriques, sans toutefois que le membre de droite soit rationnel comme avec le cosinus :

• l'identité pour la fonction sinus est :

$\sin {\bigg (}{\frac {\pi }{9}}{\bigg )}\cdot \sin {\bigg (}{\frac {2\pi }{9}}{\bigg )}\cdot \sin {\bigg (}{\frac {4\pi }{9}}{\bigg )}={\frac {{\sqrt {3}}\ }{8}}$ ;

• l'identité pour la fonction tangente (qu'on obtient en divisant l'identité pour la fonction sinus par la loi de Morrie) est :

$\tan {\bigg (}{\frac {\pi }{9}}{\bigg )}\cdot \tan {\bigg (}{\frac {2\pi }{9}}{\bigg )}\cdot \tan {\bigg (}{\frac {4\pi }{9}}{\bigg )}={\sqrt {3}}=\tan {\bigg (}{\frac {\pi }{3}}{\bigg )}$.

Généralisations

Première généralisation

La loi de Morrie est le cas particulier, où $n=3$ et $\alpha ={\frac {\pi }{9}}=20^{\circ }$, de l'identité plus générale :

$2^{n}\cdot \prod _{k=0}^{n-1}\cos(2^{k}\alpha )={\frac {\sin(2^{n}\alpha )}{\sin(\alpha )}}$

avec $\alpha \in \mathbb {C}$ et $n\in \mathbb {N} ^{*}$.

La curiosité tient au fait que si on choisit $\alpha ={\frac {\pi }{2^{n}\pm 1}}$, le membre de droite vaut ±1 (on le montre en remplaçant le dénominateur $\sin(\alpha )$ par $\sin(\pi -\alpha )$ ou $-\sin(\pi +\alpha )$), et l'égalité devient alors :

$2^{n}\cdot \prod _{k=0}^{n-1}\cos \left({\frac {2^{k}}{2^{n}\pm 1}}\pi \right)=\pm 1$.

On en tire les identités suivantes :

	$\alpha ={\frac {\pi }{2^{n}-1}}$	$\alpha ={\frac {\pi }{2^{n}+1}}$
$n=2$		$\cos \left({\frac {\pi }{5}}\right)\cdot \cos \left({\frac {2\pi }{5}}\right)={\frac {1}{4}}$
$n=3$	$\cos \left({\frac {\pi }{7}}\right)\cdot \cos \left({\frac {2\pi }{7}}\right)\cdot \cos \left({\frac {4\pi }{7}}\right)=-{\frac {1}{8}}$ $\cos \left({\frac {\pi }{7}}\right)\cdot \cos \left({\frac {2\pi }{7}}\right)\cdot \cos \left({\frac {3\pi }{7}}\right)={\frac {1}{8}}$	$\cos \left({\frac {\pi }{9}}\right)\cdot \cos \left({\frac {2\pi }{9}}\right)\cdot \cos \left({\frac {4\pi }{9}}\right)={\frac {1}{8}}$ (loi de Morrie)
$n=4$	$\cos \left({\frac {\pi }{15}}\right)\cdot \cos \left({\frac {2\pi }{15}}\right)\cdot \cos \left({\frac {4\pi }{15}}\right)\cdot \cos \left({\frac {8\pi }{15}}\right)=-{\frac {1}{16}}$	$\cos \left({\frac {\pi }{17}}\right)\cdot \cos \left({\frac {2\pi }{17}}\right)\cdot \cos \left({\frac {4\pi }{17}}\right)\cdot \cos \left({\frac {8\pi }{17}}\right)={\frac {1}{16}}$

Deuxième généralisation

La première généralisation est elle-même le cas particulier, où $b=2$, de l'identité plus générale :

$\prod _{k=0}^{n-1}\left(\sum _{j=0}^{b-1}\cos {\Big (}(b-2j-1)b^{k}\alpha {\Big )}\right)={\frac {\sin(b^{n}\alpha )}{\sin(\alpha )}}$

avec $b\in \mathbb {N} ^{*}$.

En effet, en choisissant $b=2$ le membre de gauche devient $\prod _{k=0}^{n-1}{\Big (}\cos(2^{k}\alpha )+\cos(-2^{k}\alpha ){\Big )}=\prod _{k=0}^{n-1}{\Big (}2\cos(2^{k}\alpha ){\Big )}=2^{n}\prod _{k=0}^{n-1}\cos(2^{k}\alpha )$, ce qui permet de retrouver la première généralisation.

Autres généralisations

Il existe diverses autres généralisations de la loi de Morrie, citées notamment dans un livre d'exercices de trigonométrie de 1930, telles que :

$\prod _{r=1}^{m}\cos \left({\frac {r\pi }{2m+1}}\right)=2^{-m}$

dont la loi de Morrie est le cas particulier où $m=4$.

Démonstrations

Preuve algébrique

La preuve de la loi de Morrie s'appuie sur la formule de l'angle double pour la fonction sinus :

$\sin(2\alpha )=2\sin \alpha \cos \alpha$

qui permet de trouver l'expression de $\cos(\alpha )$ et, par suite, de $\cos(2\alpha )$, $\cos(4\alpha )$ ... $\cos(2^{n-1}\alpha )$ :

${\begin{aligned}\cos \alpha &={\frac {\sin(2\alpha )}{2\sin \alpha }}\\\cos(2\alpha )&={\frac {\sin(4\alpha )}{2\sin(2\alpha )}}\\\cos(4\alpha )&={\frac {\sin(8\alpha )}{2\sin(4\alpha )}}\\&{}\,\,\,\vdots \\\cos(2^{n-1}\alpha )&={\frac {\sin(2^{n}\alpha )}{2\sin(2^{n-1}\alpha )}}.\end{aligned}}$

En multipliant toutes ces expressions les unes avec les autres, on obtient :

$\cos \alpha \cos(2\alpha )\cos(4\alpha )\cdots \cos(2^{n-1}\alpha )={\frac {\cancel {\sin(2\alpha )}}{2\sin \alpha }}\cdot {\frac {\cancel {\sin(4\alpha )}}{2\ {\cancel {\sin(2\alpha )}}}}\cdot {\frac {\cancel {\sin(8\alpha )}}{2\ {\cancel {\sin(4\alpha )}}}}\cdots {\frac {\sin(2^{n}\alpha )}{2\ {\cancel {\sin(2^{n-1}\alpha )}}}}$.

Dans la partie droite de l'expression, les numérateurs et dénominateurs intermédiaires s'éliminent deux à deux, ne laissant que le premier dénominateur $\sin \alpha$ et le numérateur final $\sin(2^{n}\alpha )$ (on dit qu'il s'agit d'un produit télescopique), ainsi qu'une puissance de 2 au dénominateur ($2^{n}$ car il y a $n$ termes) ; il vient alors :

$\prod _{k=0}^{n-1}\cos(2^{k}\alpha )={\frac {\sin(2^{n}\alpha )}{2^{n}\sin \alpha }}$,

ce qui est équivalent à la première généralisation de l'identité.

Preuves géométriques

Preuve géométrique utilisant un ennéagone.

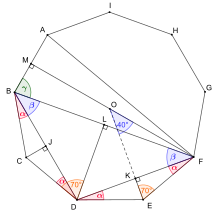
Pour démontrer les identités de la forme $2^{n}\cdot \prod _{k=0}^{n-1}\cos(2^{k}\alpha )=\pm 1$ avec $\alpha ={\frac {\pi }{2^{n}\pm 1}}$, une preuve géométrique utilisant un polygone régulier à $2^{n}\pm 1$ côtés peut être utilisée.

Ainsi, pour démontrer la loi de Morrie ($n=3$ et $\alpha ={\frac {\pi }{9}}$), une telle preuve utilisant un ennéagone régulier (9 côtés) a été publiée en 2008, puis une autre en 2015.

Cette dernière s'appuie sur l'ennéagone $ABCDEFGHI$ ci-contre, de côté 1. Soient $M$, $J$, $K$ et $L$ les milieux de $[AB]$, $[BD]$, $[DF]$ et $[BF]$, respectivement.

On montre que $\alpha ={\widehat {CBD}}={\frac {\pi }{9}}$, $\beta ={\widehat {DBF}}={\frac {2\pi }{9}}$, et $\gamma ={\widehat {FBM}}={\frac {4\pi }{9}}$.

Calcul des angles

${\widehat {DEF}}={\widehat {CDE}}={\widehat {ABC}}={\frac {7\pi }{9}}$ car ce sont des angles internes d'un ennéagone régulier.

• La somme des angles de $\triangle KEF$ vaut $\pi$, donc $\alpha =\pi -{\widehat {KEF}}-{\widehat {EKF}}=\pi -{\frac {\widehat {DEF}}{2}}-{\frac {\pi }{2}}=\pi -{\frac {7\pi }{18}}-{\frac {\pi }{2}}={\frac {\pi }{9}}$.
• ${\widehat {BDL}}={\widehat {CDL}}-\alpha ={\frac {\widehat {CDE}}{2}}-{\frac {\pi }{9}}={\frac {7\pi }{18}}-{\frac {\pi }{9}}={\frac {5\pi }{18}}$.
  La somme des angles de $\triangle BDL$ vaut $\pi$, donc $\beta =\pi -{\widehat {BDL}}-{\widehat {BLD}}=\pi -{\frac {5\pi }{18}}-{\frac {\pi }{2}}={\frac {2\pi }{9}}$.
• $\gamma ={\widehat {ABC}}-\alpha -\beta ={\frac {7\pi }{9}}-{\frac {\pi }{9}}-{\frac {2\pi }{9}}={\frac {4\pi }{9}}$.

$\triangle KEF$ est rectangle en $K$, donc ${\textstyle \cos(\alpha )={\frac {|KF|}{|EF|}}}$. Or $|DF|=2\cdot |KF|$ car $K$ est milieu de $[DF]$, donc :

$|DF|=2\cdot |EF|\cdot \cos \left({\frac {\pi }{9}}\right)$.

$\triangle DFL$ est rectangle en $L$, donc ${\textstyle \cos(\beta )={\frac {|LF|}{|DF|}}}$. Or $|BF|=2\cdot |LF|$ car $L$ est milieu de $[BF]$, donc :

$|BF|=2\cdot |DF|\cdot \cos \left({\frac {2\pi }{9}}\right)$.

$\triangle BFM$ est rectangle en $M$, donc ${\textstyle \cos(\gamma )={\frac {|BM|}{|BF|}}}$. Or $|AB|=2\cdot |BM|$ car $M$ est milieu de $[AB]$, donc :

$|AB|=2\cdot |BF|\cdot \cos \left({\frac {4\pi }{9}}\right)$.

Or $|AB|=|EF|=1$ car ce sont des côtés de l'ennéagone, et en remplaçant $|BF|$ et $|DF|$ par les expressions ci-dessus, on obtient :

$1=2\cdot 2\cdot 2\cdot \cos \left({\frac {\pi }{9}}\right)\cdot \cos \left({\frac {2\pi }{9}}\right)\cdot \cos \left({\frac {4\pi }{9}}\right)$, d'où la loi de Morrie.

Les auteurs de cette preuve ont par la suite publié, en 2016, une preuve géométrique de l'identité où $n=3$ et $\alpha ={\frac {\pi }{7}}$, en utilisant un heptagone régulier (7 côtés).

De même, l'identité où $n=2$ et $\alpha ={\frac {\pi }{5}}$ peut être prouvée en utilisant un pentagone régulier (5 côtés).

Bibliographie

Source primaire :

• (en) James Gleick, Genius : The Life and Science of Richard Feynman, New York, Pantheon Books, 1992, 532 p. (ISBN 0-679-40836-3, lire en ligne).

Sources secondaires centrées :

• (en) Ernest C. Anderson, « Morrie's Law and Experimental Mathematics », Journal of Recreational Mathematics, vol. 29, n^o 2,‎ 1998, p. 85–88.
• (en) Eric W. Weisstein, « Morrie's Law », sur MathWorld.
• (en) Glen Van Brummelen, « Morrie's Law and friends », dans Trigonometry : A Very Short Introduction, Oxford, Oxford University Press, coll. « Very Short Introductions Series » (n^o 626), 2020, 163 p. (ISBN 978-0-19-881431-3, DOI 10.1093/actrade/9780198814313.001.0001), p. 79–83 [lire en ligne].

Généralisations :

• (en) William A. Beyer, James D. Louck et Doron Zeilberger, « Math Bite : A Generalization of a Curiosity that Feynman Remembered All His Life », Mathematics Magazine, vol. 69, n^o 1,‎ février 1996, p. 43–44 (DOI 10.2307/2691393, JSTOR 2691393, MR 1573132, lire en ligne).
• (en) Garry J. Tee, « Math Bite : Further Generalizations of a Curiosity that Feynman Remembered All His Life », Mathematics Magazine, vol. 72, n^o 1,‎ février 1999, p. 44 (DOI 10.1080/0025570X.1999.11996697, JSTOR 2691313, MR 1573369, lire en ligne).
• (en) Gaston Brouwer, « A Generalization of the Angle Doubling Formulas for Trigonometric Functions », Mathematics Magazine, vol. 90, n^o 1,‎ février 2017, p. 12–18 (DOI 10.4169/math.mag.90.1.12, JSTOR 10.4169/math.mag.90.1.12, MR 3608695).

Preuves géométriques :

• (en) David Miles et Chris Pritchard, « Three Trigonometric Results from a Regular Nonagon », Mathematics in School, vol. 37, n^o 5,‎ novembre 2008, p. 12–13 (JSTOR 30212315).
• (en) Samuel G. Moreno et Esther M. García-Caballero, « A Geometric Proof of Morrie's Law », The American Mathematical Monthly, vol. 122, n^o 2,‎ février 2015, p. 168 (DOI 10.4169/amer.math.monthly.122.02.168, JSTOR 10.4169/amer.math.monthly.122.02.168, MR 3324692).
• (en) Samuel G. Moreno et Esther M. García-Caballero, « A Geometric Proof of Morrie's Law », The American Mathematical Monthly, vol. 122, n^o 3,‎ mars 2015, p. 233 (DOI 10.4169/amer.math.monthly.122.03.233, JSTOR 10.4169/amer.math.monthly.122.03.233, MR 3327712).
• (en) Samuel G. Moreno et Esther M. García-Caballero, « A Geometric Proof of a Morrie-Type Formula », Mathematics Magazine, vol. 89, n^o 3,‎ juin 2016, p. 214–215 (DOI 10.4169/math.mag.89.3.214, MR 3519084).