Ordre des cours d'eau
L'ordre des cours d'eau est un nombre entier positif utilisé en géomorphologie et en hydrologie pour indiquer le niveau de branchement dans un système hydrographique.
Il existe différentes approches[1] pour la hiérarchisation topologique des rivières ou des sections de rivières en fonction de leur distance à partir de la source ("top-down" ou du haut vers le bas[2]) ou à partir de la confluence (le point de fusion de deux rivières) ou de l’embouchure de la rivière ("bottom-up" ou du bas vers le haut[3]), et leur position hiérarchique dans le système hydrographique.
En ce qui concerne la terminologie, les mots de "ruisseau" ou "bras" sont utilisés de préférence à celui de "rivière".
Ordre classique
modifier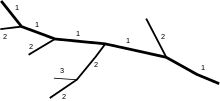
L'ordre classique des cours d'eau, également appelé ordre des cours d'eau de Hack[4] ou de Gravelius, est une hiérarchie "ascendante" qui attribue le nombre "1" (ordre 1) au fleuve dont l'embouchure est à la mer (le cours d'eau principal ou "de premier ordre"). On donne à ses affluents un nombre augmenté de 1 par rapport à celui de la rivière ou ruisseau dans lequel ils se déversent. Ainsi, par exemple, tous les affluents immédiats du cours d'eau principal reçoivent le numéro "2". Les affluents se vidant dans un "2" reçoivent le numéro "3" et ainsi de suite[5].
Commençant à l'embouchure, cet ordre de cours d'eau indique l'emplacement de la rivière dans le réseau. Il est utile à des fins cartographiques générales, mais peut poser un problème car, à chaque confluence, il faut décider laquelle des deux branches est la continuation du chenal principal ou si le chenal principal a sa source au confluent de deux autres ruisseaux plus petits. Le premier ordre est celui qui, à chaque confluence, présente le plus grand débit volumétrique, ce qui correspond généralement à la dénomination ancienne des rivières. La recherche par les géographes du XIXe siècle de la "vraie" source d'une rivière était associée à ce système d'ordination des cours d'eau. La recherche avançant, d'autres critères ont été discutés pour permettre de définir le cours d'eau principal. Outre le ruisseau ayant la plus grande longueur (la source se trouvant à la distance maximale de l'embouchure) et la taille des divers bassins versants, il a été tenu compte du ruisseau qui s'écartait le moins de la confluence réelle, ainsi que des simples noms successifs de rivières, tels que le Rhin et l'Aar ou l'Elbe et la Vltava.
Ordre de Strahler
modifier
D'après le système top-down mis au point par Strahler, les rivières de premier ordre sont les affluents ultimes. Si deux cours d'eau du même ordre fusionnent, le cours d'eau résultant reçoit un ordre supérieur de 1. Si deux rivières avec des ordres différents fusionnent, le cours d'eau résultant reçoit le plus élevé des deux ordres[6],[7].
L’ordre de Strahler est conçu pour la morphologie d’un bassin et constitue la base d’importants indicateurs hydrographiques de sa structure, tels que le taux de bifurcation, la densité et la fréquence de drainage. Sa base est la ligne de partage des eaux du bassin versant. Il dépend toutefois de l'échelle : plus l'échelle de la carte est grande, plus nombreux sont les ordres qui peuvent être révélés. Une limite inférieure générale pour la définition d'un "cours d'eau" peut être définie en définissant sa largeur à l'embouchure ou, en se référant à la carte, en limitant son étendue. Le système lui-même est également utilisable pour les structures à petite échelle.
Le nombre de Strahler atteint :
| Nom | Nombre | |
|---|---|---|
| Fleuve | Strahler[8] | |
| Amazone | 12 | |
| Mississippi | 10 | |
| Nil | 10 | |
| Rhône | 9 | |
| Garonne | 9 | |
| Ienissei | 8 | |
| Danube | 8 | |
| Loire | 8 | |
| Congo | 7 | |
| Indus | 7 | |
| Mékong | 7 | |
| Rhin | 7 | |
| Seine | 7 | |
| Adour | 7 | |
| Dordogne | 7 | |
| Meuse | 7 | |
| Aar | 6 | |
| Oise | 6 | |
| Tamise | 5 | |
| Tibre | 5 | |
| Marne | 5 | |
| Lot | 5 | |
Ordre de Shreve
modifier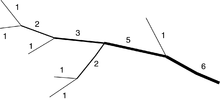
Le système de Shreve[9] a également attribué l'ordre "1" aux affluents les plus ultrapériphériques. À la confluence cependant, les numéros de rangs des cours d'eau sont cette fois additionnés[10]. Par exemple deux cours d'eau de rang "3" qui confluent donneront un cours de rang "6" en ordre de Shreve, mais un cours de rang "4" en ordre de Strahler.
L’ordre de Shreve est privilégié en hydrodynamique : il additionne le nombre de sources dans chaque bassin versant au-dessus d’une jauge ou d’un débit, et correspond approximativement aux volumes de rejet et aux niveaux de pollution. Comme la méthode de Strahler, elle dépend de la précision des sources incluses, mais moins de l’échelle de la carte. Cette ordination peut être rendue relativement indépendante de l'échelle en utilisant une normalisation appropriée et est donc en grande partie indépendante d'une connaissance exacte des couches supérieure et inférieure d'une zone[10].
Le nombre de Shreve atteint :
| Nom | Nombre | |
|---|---|---|
| Fleuve | Shreve | |
| Amazone | Au moins 29 | |
| Mississippi | Au moins 23 | |
| Nil | Au moins 22 | |
| Rhône | Au moins 20 | |
| Indus | Au moins 19 | |
| Mékong | Au moins 19 | |
| Congo | Au moins 18 | |
| Ienissei | Au moins 18 | |
| Rhin | Au moins 18 | |
| Aar | Au moins 17 | |
| Garonne | Au moins 16 | |
| Loire | Au moins 16 | |
| Oise | Au moins 16 | |
| Seine | Au moins 16 | |
| Danube | Au moins 15 | |
| Adour | Au moins 14 | |
| Dordogne | Au moins 14 | |
| Marne | Au moins 14 | |
| Meuse | Au moins 14 | |
| Lot | Au moins 13 | |
| Tamise | Au moins 11 | |
| Tibre | Au moins 9 | |
Ordre de Horton et autres systèmes
modifierParmi les autres systèmes, on trouve l’ordre de Horton, un système précoce, top-down (du haut vers le bas), conçu par Robert Horton[11], et le système d'ordre de cours d'eau topologique qui est bottom-up (du bas vers le haut) et où le numéro d'ordre de flux augmente de 1 à chaque confluence[5].
Ordre classique vs méthodes de Horton & Strahler
modifierLes systèmes d’ordination classique ou topologique se voient attribuer un ordre numérique sans dimension, commençant à 1 à l’embouchure d’un cours d’eau qui est son point d’altitude le plus bas. L'ordre vectoriel augmente ensuite à mesure qu'il trace en amont et qu'il converge avec d'autres cours d'eau plus petits, ce qui entraîne une corrélation des nombres d'ordre les plus élevés avec l'élévation plus élevée des eaux d'amont. Horton a proposé d'inverser cette ordination : son rapport de recherche de 1947 établissait une méthode d'ordination basée sur la géométrie vectorielle. Cinq ans plus tard, en 1952, Arthur Strahler proposa une modification de la méthode de Horton. Les méthodes de Horton et Strahler ont toutes deux établi l’attribution de l’ordre le plus bas au numéro 1, en commençant par le cours supérieur de la rivière, qui est le point d’altitude le plus élevé. Alors que l'attribution classique est corrélée à la hauteur et à l'altitude et suit un tracé vers l'amont, les méthodes d'ordination de Horton et Strahler sont corrélées à l'écoulement par gravité et suivent un tracé vers l'aval.
Les méthodes de Horton et de Strahler reposent toutes deux sur les principes de la géométrie vectorielle points-lignes. Les règles de Horton et de Strahler constituent la base des algorithmes de programmation qui interprètent les données cartographiques mises en requête dans les systèmes d'information géographique.
Utilisation
modifierL’utilisation classique de l’ordre des cours d'eau se fait en général en cartographie hydrologique. Les systèmes d’ordination des cours d’eau sont également importants pour la cartographie systématique d’un système fluvial, ce qui permet d’étiqueter et de classer les cours d’eau de façon claire.
Les méthodes de Strahler et de Shreve sont particulièrement utiles pour la modélisation et l'analyse morphométrique des systèmes fluviaux, car elles définissent chaque section d'une rivière. Cela permet de séparer le réseau à chaque jauge ou sortie en régimes amont et aval et de classer ces points. Elles servent également de base à la modélisation du bilan hydrique à l’aide de modèles de stockage ou temps-débit, flux de précipitations, etc.
Dans les sciences naturelles basées sur les SIG, ces deux modèles sont utilisés car ils montrent l'étendue graphique d'un objet fluvial.
Les activités de recherche qui ont suivi le rapport de Strahler de 1952 ont été axées sur la résolution de certains problèmes survenant lors de la conversion de cartes bidimensionnelles en modèles vectoriels tridimensionnels. Un défi a été de convertir les images pixel rasterisées des cours d'eau en format vectoriel. Un autre problème a été que les ajustements d'échelle de la carte lors de l'utilisation du SIG peuvent altérer la classification des cours d'eau par un facteur d'un ou deux ordres. Selon l’échelle de la carte SIG, certains détails de la structure arborescente d’un réseau hydrographique peuvent être perdus.
Les efforts de recherche menés par le secteur privé, les universités et des organismes gouvernementaux fédéraux tels que l’EPA et l’USGS ont combiné leurs ressources et concentré leurs attentions sur ces problèmes ainsi que d'autres. L'intention principale est de normaliser les règles de logiciel et de programmation afin que les données SIG soient toujours fiables à n'importe quelle échelle de carte. Dans cette optique, l’EPA et l’USGS ont mené des travaux de standardisation qui ont abouti à la création de la Carte Nationale aux États-Unis (The National Map). Les deux agences fédérales, ainsi que les principales sociétés de développement de logiciels du secteur privé, ont adopté les principes vectoriels d’ordination des cours d'eau de Horton et Strahler comme base des règles de logique de codage intégrées au logiciel standardisé National Map.
Notes et références
modifier- (de) Thomas Koschitzki, GIS-basierte, automatische Erfassung natürlicher Fließgewässerhierarchien und ihre Abbildung in Datenbanken, beispielhaft dargestellt am Einzugsgebiet der Salza., Halle (Saale), Martin-Luther-Universität Halle-Wittenberg, (lire en ligne), p. 12
- (en) Lee Weishar, « Development of Marsh Hydrogeomorphology and Marsh Vegetation with a Salt Hay Farm Wetland Restoration Site » [PDF], sur wisc.edu, (consulté le ), p. 30
- (en) Lee Weishar, « Development of Marsh Hydrogeomorphology and Marsh Vegetation with a Salt Hay Farm Wetland Restoration Site » [PDF], sur wisc.edu, (consulté le ), p. 35
- (en) J. Hack, « Studies of longitudinal stream profiles in Virginia and Maryland », U.S. Geological Survey Professional Paper, , p. 294-B (lire en ligne [PDF])
- (en) Jarek Jasiewicz, « Module R "stream.order" », sur svn.osgeo.org (consulté le )
- (en) Arthur N. Strahler, « Quantitative analysis of watershed geomorphology », Eos, Transactions American Geophysical Union, vol. 38, no 6, , p. 913–920 (ISSN 2324-9250, DOI 10.1029/TR038i006p00913, lire en ligne, consulté le )
- (en) A. N. Strahler, « Quantitative geomorphology of drainage basins and channel networks. », Handbook of Applied Hydrology, New York: McGraw-Hill, V. T. Chow, , p. 4-39, 4-76 (lire en ligne [PDF])
- (en) Colbert E. Cushing, Kenneth W. Cummins et G. Wayne Minshall, River and Stream, Londres, University of California press, coll. « Ecosystems of the world », , 825 p. (ISBN 0-520-24567-9, lire en ligne), p. 390
- Système de Shreve : du nom du géomorphologue Ronald L. Shreve, des Universités de Chicago et de Seattle, dont on pourra consulter plusieurs articles sur le site suivant, notamment celui-ci qui concerne le thème de l'article : (en) Ronald L. Shreve, « Statistical Law of Stream Numbers » [« Loi statistique des nombres de flux (= des rangs dans l'arborescence des cours d'eau) »], The Journal of Geology, vol. 74, no 1, (lire en ligne, consulté le ). Et ici, une liste de ses contributions plus récentes : (en) « Ronald L. Shreve's research while affiliated with University of Washington Seattle and other places » [« Recherches/Publications de Ronald L. Shreve durant son affiliation à l'Université de Seattle, état de Washington, et ailleurs »], sur researchgate.net, 1986-2011 (consulté le ).
- Ronald L. Shreve, « Statistical Law of Stream Numbers », The Journal of Geology, vol. 74, no 1, , p. 17–37 (ISSN 0022-1376, DOI 10.1086/627137, lire en ligne, consulté le )
- (en) Robert E. Horton, « EROSIONAL DEVELOPMENT OF STREAMS AND THEIR DRAINAGE BASINS; HYDROPHYSICAL APPROACH TO QUANTITATIVE MORPHOLOGY », GSA Bulletin, vol. 56, no 3, , p. 275–370 (ISSN 0016-7606, DOI 10.1130/0016-7606(1945)56[275:EDOSAT]2.0.CO;2, lire en ligne, consulté le )
Voir aussi
modifierLiens externes
modifier- Glossaire International de l'Hydrologie
- Ordres de Cours d'Eau pour le Réseau Hydrographique Numérisé de Suisse

