Théorème du séparateur planaire

En théorie des graphes, le théorème du séparateur planaire, stipule que tout graphe planaire peut être divisé en parties plus petites en supprimant un petit nombre de sommets. Plus précisément, le théorème affirme qu'il existe un ensemble de $O({\sqrt {n}})$ sommets d'un graphe à $n$ sommets dont la suppression partitionne le graphe en sous-graphes disjoints dont chacun a au plus $2n/3$ sommets.

Présentation

Une forme plus faible du théorème séparateur avec un séparateur de taille $O({\sqrt {n}}\log ^{3/2}n)$ au lieu de $O({\sqrt {n}})$ a été prouvée à l'origine par Ungar (1951), et la forme avec la borne asymptotique plus fine sur la taille du séparateur a été prouvée pour la première fois par Lipton & Tarjan (1979). Depuis leurs travaux, le théorème du séparateur a été redémontré de plusieurs manières différentes, la constante dans le terme en $O({\sqrt {n}})$ du théorème a été amélioré, et le théorème a été étendu à certaines classes de graphes non planaires.

L'application itérée du théorème du séparateur produit une hiérarchie de séparateurs qui peut prendre la forme soit d'une décomposition arborescente, soit d'une décomposition en branches du graphe. Les hiérarchies de séparateurs peuvent être utilisées pour concevoir des algorithmes de diviser pour régner efficaces pour les graphes planaires, et la programmation dynamique sur ces hiérarchies peut être utilisée pour des algorithmes en temps exponentiel et traitable en complexité paramétrée pour résoudre des problèmes d'optimisation NP-difficiles sur ces graphes. Les hiérarchies de séparateurs peuvent également être utilisées dans la dissection imbriquée, une variante efficace de l'élimination de Gauss-Jordan pour résoudre des systèmes systèmes d' équations linéaires creux résultant de méthodes d' éléments finis.

Au-delà des graphes planaires, les théorèmes de séparation ont été appliqués à d'autres classes de graphes, y compris les graphes excluant un mineur, les graphes du plus proche voisin et les maillages d'éléments finis. L'existence d'un théorème séparateur pour une classe de graphes peut être formalisée et quantifiée par les concepts de largeur arborescente d'arbre d'expansion polynomial.

Énoncé du théorème

Le théorème du séparateur planaire est le suivant :

Théorème — Dans tout graphe planaire $G=(V,E)$ à $n$ sommets, il existe une partition des sommets de $G$ en trois ensembles $A$, $S$ et $B$ telle que $A$ et $B$ ont chacun au plus $2n/3$ éléments, $S$ a $O({\sqrt {n}})$ éléments, et il n'y a pas d'arête entre des sommets de $A$ et de $B$.

Dans cet énoncé il n'est pas requis que $A$ ou $B$ forment des sous-graphes connexes de $G$. L'ensemble $S$ est appelé le séparateur de cette partition.

Une formulation équivalente est que les arêtes d'un graphe planaire à $n$ sommets $G$ peuvent être partagées en arêtes de deux sous-graphes à arêtes disjointes $G_{1}$ et $G_{2}$ de sorte que chacun des deux sous-graphes a au moins $n/3$ sommets et que l'intersection des ensembles de sommets des deux sous-graphes a $O({\sqrt {n}})$ sommets. Une telle partition est connue sous le nom de séparation. Pour une séparation donnée, l'intersection des deux ensembles de sommets forme un séparateur, et les sommets qui appartiennent à l'un des sous-graphes mais pas à l'autre forment des sous-ensembles séparés ayant chacun au plus $2n/3$ sommets. Réciproquement, pour une partition en trois ensembles $A$, $S$ et $B$ satisfaisant les conditions du théorème du séparateur planaire, on peut former une séparation dans laquelle les arêtes avec une extrémité dans $A$ appartiennent à $G_{1}$, les arêtes avec une extrémité dans $B$ appartiennent à $G_{2}$, et les arêtes restantes (avec les deux extrémités dans $S$) sont réparties arbitrairement.

La constante $2/3$ dans l'énoncé du théorème du séparateur est arbitraire et peut être remplacée par tout autre nombre dans l'intervalle ouvert $(1/2,1)$ sans changer l'énoncé du théorème : une partition en sous-ensembles de taille plus équilibrée peut être obtenue, à partir d'une partition déséquilibrée, en divisant à plusieurs reprises le plus grand des ensembles de la partition et en regroupant les composants connexes résultantes.

Exemple

Un séparateur planaire pour un graphe grille

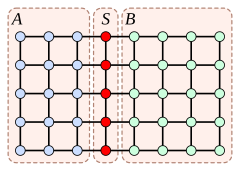
Considérons un graphe grille avec $r$ lignes et $c$ colonnes ; le nombre $n$ de sommets est égal $rc$. Dans l'exemple, on a $r=5$, $c=8$, et $n=rc=40$. Si $r$ est impair, il y a une seule ligne centrale, et sinon il y a deux lignes près du centre ; de même, si $c$ est impair, il y a une seule colonne centrale, et sinon il y a deux colonnes près du centre. Si on prend pour $S$ l'une de ces lignes ou colonnes centrales, et on supprime $S$ du graphe, on partitionne le graphe en deux sous-graphes connexes plus petits $A$ et $B$, dont chacun a au plus $n/2$ sommets. Si $r\leq c$ (comme dans l'illustration), le choix d'une colonne centrale donne un séparateur $S$ avec $r\leq {\sqrt {n}}$ sommets, et de même si $c\leq r$ le choix d'une ligne centrale donne un séparateur avec au plus ${\sqrt {n}}$ sommets. Ainsi, chaque graphe grille a un séparateur $S$ de taille au plus ${\sqrt {n}}$, dont la suppression partitionne le graphe en deux composantes connexes qui chacune est de taille au plus $n/2$.

Le théorème du séparateur planaire stipule qu'une partition similaire peut être construite dans n'importe quel graphe planaire. Le cas des graphes planaires arbitraires diffère du cas des graphes grille en ce que le séparateur a une taille en $O({\sqrt {n}})$ qui peut être plus grande que ${\sqrt {n}}$, et que la borne sur la taille des deux sous-ensembles $A$ et $B$ (dans les versions les plus courantes du théorème) est $2n/3$ plutôt que $n/2$, et que les deux sous-ensembles $A$ et $B$ ne forment pas nécessairement des sous-graphes connexes.

Constructions

Superposition en largeur

Lipton & Tarjan (1979) augmentent le graphe planaire donné par des arêtes supplémentaires, si nécessaire, afin qu'il devienne planaire maximal (chaque face d'un plongement planaire est un triangle). Ils effectuent ensuite un parcours en largeur, à partir d'un sommet arbitraire $v$, et partitionnent les sommets en niveaux par leur distance à $v$.

Si $l_{1}$ est le niveau médian (c'est-à-dire le niveau tel que les nombres de sommets aux niveaux supérieur et inférieur sont tous deux au plus $n/2$), alors il existe des niveaux $l_{0}$ et $l_{2}$ qui sont à $O({\sqrt {n}})$ étapes au-dessus et au-dessous de $l_{1}$ respectivement et qui contiennent $O({\sqrt {n}})$ sommets respectivement, car sinon il y aurait plus de $n$ sommets dans les niveaux proches de $l_{1}$.

Les auteurs montrent qu'il existe un séparateur $S$ formé par l'union des niveaux $l_{0}$ et $l_{2}$, par les d'extrémités des arêtes $e$ de $G$ qui n'appartiennent pas à l'arbre de recherche en largeur et qui se trouvent entre les deux niveaux, et par les sommets sur les deux chemins de l'arbre de recherche en largeur depuis les points d'extrémité de $e$ en remontant jusqu'au niveau $l_{0}$. La taille du séparateur $S$ ainsi construit est au plus de ${\sqrt {8n}}\approx 2,83{\sqrt {n}}$. Les sommets du séparateur et des deux sous-graphes disjoints peuvent être trouvés en temps linéaire.

Cette preuve du théorème du séparateur s'applique également aux graphes planaires pondérés, dans lesquels chaque sommet a un coût non négatif. Le graphe peut être divisé en trois ensembles $A$, $S$, et $B$ tels que $A$ et $B$ ont chacun un coût au plus égal à $2/3$ du coût total et $S$ possède $O({\sqrt {n}})$ sommets, sans arêtes de $A$ et de $B$. Une analyse plus fine d'une construction de séparateur similaire a permis à Djidjev (1982) de montrer que la borne sur la taille de $S$ peut être réduite à ${\sqrt {6n}}\approx 2.45{\sqrt {n}}$.

Holzer et al. (2009) proposent une version simplifiée de cette approche : ils augmentent le graphe pour qu'il soit planaire maximal et construisent un arbre de recherche de largeur d'abord comme précédemment. Ensuite, pour chaque arête $e$ qui ne fait pas partie de l'arbre, ils forment un cycle en combinant $e$ avec le chemin de l'arbre qui relie ses points d'extrémité. Ils utilisent ensuite comme séparateur les sommets d'un de ces cycles. Bien que cette approche ne trouve pas toujours un petit séparateur pour les graphes planaires de grand diamètre, leurs expériences indiquent qu'elle surpasse les méthodes de superposition en largeur de Lipton-Tarjan et Djidjev sur de nombreux types de graphes planaires.

Séparateurs de cycles simples

Pour un graphe planaire qui est maximal, on peut faire une construction plus précise, à savoir un séparateur par cycle simple ; c'est un cycle simple de petite longueur tel que l'intérieur et l'extérieur du cycle, dans l'unique plongement planaire du graphe, ont chacun au plus $2n/3$ sommets. Miller (1986) a montré cette construction (avec un séparateur de taille ${\sqrt {8n}}$) en utilisant la technique de Lipton-Tarjan dans une version modifiée de la recherche en largeur dans laquelle les niveaux de la recherche forment des cycles simples.

Alon, Seymour & Thomas (1994) prouvent l'existence de séparateurs de cycles simples plus directement : ils considèrent un cycle $C$ d'au plus ${\sqrt {8n}}$ sommets, avec au plus $2n/3$ sommets à l'extérieur de $C$, qui forme une partition de l'intérieur et de l'extérieur aussi régulière que possible, et ils montrent que ces hypothèses impliquent que $C$ est un séparateur. En effet, sinon les distances à l'intérieur de $C$ doivent être égales aux distances dans le disque extérieur par $C$ (car un chemin plus court à l'intérieur du disque ferait partie du contour d'un cycle meilleur). De plus, $C$ doit avoir une longueur exactement égale à ${\sqrt {8n}}$, car sinon il pourrait être amélioré en remplaçant l'une de ses arêtes par les deux autres côtés d'un triangle. Si les sommets de $C$ sont numérotés de $1$ à ${\sqrt {8n}}$ dans le sens des aiguilles d'une montre, et que le sommet $i$ est apparié au sommet ${\sqrt {8n}}-i+1$, alors ces paires appariées peuvent être reliées par des chemins disjoints de sommets à l'intérieur du disque, par une variante du théorème de Menger pour les graphes planaires. Cependant, la longueur totale de ces chemins serait nécessairement supérieure à $n$, une contradiction. Avec quelques arguments supplémentaires, les auteurs montrent par une méthode similaire qu'il existe un séparateur de cycles simple de taille au plus ${\sqrt {9n/2}}\approx 2,12{\sqrt {n}}$.

Djidjev & Venkatesan (1997) ont amélioré le facteur constant dans le théorème du séparateur de cycle simple à $1,97{\sqrt {n}}$. Leur méthode peut également trouver des séparateurs de cycles simples pour des graphes avec des poids de sommets non négatifs, avec une taille de séparateur d'au plus $2{\sqrt {n}}$, et peut engendrer des séparateurs de taille plus petite au prix d'une partition plus inégale du graphe.

Dans un graphe planaire biconnexe qui n'est pas maiximal, il existe des séparateurs de cycles simples dont la taille est proportionnelle à la norme euclidienne du vecteur des longueurs des faces et qui peuvent être trouvés en un temps quasi-linéaire.

Séparateurs de cercle

Selon le théorème d'empilement de cercles (aussi connu sous le nom de théorème de Koebe, Andreev et Thurston, tout graphe planaire peut être représenté par un empilement de disques circulaires dans le plan avec des intérieurs disjoints, de sorte que deux sommets du graphe sont adjacents si et seulement si les disques de la paire correspondante sont tangents. Miller et al. (1997) ont montré que, pour un tel empilement, il existe un cercle qui est touche par au plus $3n/4$ disques tangents à l'intérieur, ou au plus $3n/4$ disques à l'extérieur, et qui croise $O({\sqrt {n}})$ disques.

Pour le prouver, Miller et al. utilisent une projection stéréographique pour projeter l'empilement sur la surface d'une sphère unitaire en trois dimensions. En choisissant soigneusement la projection, le centre de la sphère peut être transformé en un point central des centres du disque sur la surface, de sorte que tout plan passant par le centre de la sphère la divise en deux demi-espaces qui contiennent ou croisent chacun au plus $3n/4$ des disques. Si un plan passant par le centre est choisi uniformément au hasard, un disque sera croisé avec une probabilité proportionnelle à son rayon. Par conséquent, le nombre moyen de disques croisés est proportionnel à la somme des rayons des disques. Cependant, la somme des carrés des rayons est proportionnelle à la surface totale des disques, qui est au plus la surface totale de la sphère unité, qui elle est une constante. Un argument impliquant l'inégalité de Jensen montre que, lorsque la somme des carrés de $n$ nombres réels non négatifs est borné par une constante, la somme des nombres eux-mêmes est $O({\sqrt {n}})$. Par conséquent, le nombre moyen de disques traversés par un plan aléatoire est $O({\sqrt {n}})$ et il existe un plan qui traverse au plus ce nombre de disques. Ce plan coupe la sphère dans un grand cercle, qui se projette en un cercle dans le plan avec les propriétés souhaitées. Les disques traversés par ce cercle, au nombre de $O({\sqrt {n}})$, correspondent aux sommets d'un séparateur de graphe planaire qui sépare les sommets dont les disques sont à l'intérieur du cercle des sommets dont les disques sont à l'extérieur du cercle, avec au plus $3n/4$ sommets dans chacun de ces deux sous-ensembles.

La méthode utilisée conduit à un algorithme randomisé pour trouver un tel séparateur en temps linéaire et un algorithme déterministe moins pratique avec la même borne de temps linéaire . On peut montrer que l'algorithme trouve des séparateurs de taille au plus

${\sqrt {\frac {2\pi }{\sqrt {3}}}}\left({\frac {1+{\sqrt {3}}}{2{\sqrt {2}}}}+o(1)\right){\sqrt {n}}\approx 1.84{\sqrt {n}}$.

Bien que cette majoration améliorée de la taille de séparateur se fasse au détriment d'une partition plus inégale du graphe, Spielman & Teng (1996) constatent qu'elle fournit un meilleur facteur constant du temps pour la dissection imbriquée par rapport aux séparateurs d' Alon, Seymour & Thomas (1990) . La taille des séparateurs qu'il produit peut encore être améliorée, en pratique, en utilisant une répartition non uniforme des plans de coupe aléatoires.

La projection stéréographique dans l'argument de Miller et al. ci-dessus peut être contournée en considérant le plus petit cercle contenant une fraction constante des centres des disques, puis en l'étendant par une constante choisie uniformément dans la plage $[1,2]$. Comme dans Miller et al., les disques coupant le cercle élargi forment un séparateur valide et le séparateur est de la bonne taille en moyenne. Les constantes résultantes sont en revanche un peu moins bonnes.

Séparateurs d'arêtes

Une variante du théorème du séparateur planaire implique des séparateurs d'arêtes, qui sont de petits ensembles d'arêtes formant une coupe entre deux sous-ensembles $A$ et $B$ de sommets du graphe. Les deux ensembles $A$ et $B$ doivent chacun avoir une taille au plus égale à une fraction constante du nombre $n$ de sommets du graphe (par convention, les deux ensembles ont une taille au plus $2n/3$), et chaque sommet du graphe appartient exactement à l'un des ensembles $A$ et $B$. Le séparateur est composé des arêtes qui ont une extrémité dans $A$ et une autre dans $B$. Les bornes sur la taille d'un séparateur d'arêtes dépendent du degré des sommets ainsi que du nombre de sommets dans le graphe : les graphes planaires dans lesquels un sommet a un degré $n-1$, y compris les graphes roue et les graphes étoile, n'ont pas de séparateur d'arêtes avec un nombre sous-linéaire d'arêtes, car tout séparateur d'arêtes devrait inclure toutes les arêtes reliant le sommet de grand degré aux autres sommets de la coupe. Cependant, tout graphe planaire de degré maximum $\delta$ a un séparateur de bord de taille $O({\sqrt {\delta n}})$ .

Papadimitriou & Sideri (1996) décrivent un algorithme en temps polynomial pour trouver le plus petit séparateur d'arêtes qui partitionne un graphe $G$ en deux sous-graphes de taille égale, lorsque $G$ est un sous-graphe induit d'un graphe grille sans trous ou avec un nombre constant de trous. Cependant, ils conjecturent que le problème est NP-complet pour les graphes planaires arbitraires, et ils montrent que la complexité du problème est la même pour les graphes grille avec un nombre arbitraire de trous que pour les graphes planaires arbitraires.

Bornes inférieures

Un polyèdre formé en remplaçant chacune des faces d'un icosaèdre par un maillage de 100 triangles, un exemple de la construction minorante de Djidjev (1982)

Dans un graphe grille ${\sqrt {n}}\times {\sqrt {n}}$, un ensemble $S$ de $s<{\sqrt {n}}$ les points peut inclure un sous-ensemble d'au plus $s(s-1)/2$ points de grille, et le maximum est atteint en disposant $S$ en diagonale près d'un coin de la grille. Par conséquent, afin de former un séparateur qui sépare au moins $n/3$ des points de la grille restante, $s$ doit être au moins égal à ${\sqrt {2n/3}}\approx 0.82{\sqrt {n}}$.

Il existe pour tout $n$ des graphes planaires à $n$ sommets tels que tout séparateur $S$ qui partitionne le graphe restant en sous-graphes d'au plus $2n/3$ sommets a une taille au moins égale à ${\sqrt {4\pi n/{\sqrt {27}}}}\approx 1.56{\sqrt {n}}$. La construction consiste à approximer une sphère par un polyèdre convexe, à remplacer chacune des faces du polyèdre par un maillage triangulaire, et à appliquer un des théorèmes isopérimétriques à la surface de la sphère.

Autres classes de graphes

Certains graphes peu denses n'ont pas de séparateurs de taille sous-linéaire : ainsi, dans un graphe d'expansion, la suppression d'une fraction constante de sommets ne laisse toujours qu'une seule composante connexe.

Un des plus anciens théorèmes de séparation connus est peut-être le résultat de Jordan (1869) selon lequel tout arbre peut être divisé en sous-arbres d'au plus $n/2$ sommets chacun par la suppression d'un seul sommet. En particulier, le sommet qui minimise la taille maximale des composants a cette propriété, car sinon son voisin dans l'unique grand sous-arbre formerait une partition encore meilleure. En appliquant la même technique à une décomposition arborescente d'un graphe arbitraire, il est possible de montrer que tout graphe possède un séparateur de taille au plus égale à sa largeur arborescente.

Un graphe $G$ qui n'est pas planaire, mais qui peut être plongé sur une surface de genre $g$, possède un séparateur avec $O({\sqrt {gn}})$ sommets, comme l'ont prouvé Gilbert, Hutchinson & Tarjan (1984) en utilisant une approche similaire à celle de Lipton & Tarjan (1979). Ils regroupent les sommets du graphe en niveaux dans un parcours en largeur et trouvent deux niveaux dont la suppression laisse au plus un grand composant composé d'un petit nombre de niveaux. Ce composant restant peut être rendu planaire en supprimant un certain nombre de chemins du parcours en largeur proportionnels au genre, puis la méthode de Lipton & Tarjan peut être appliquée au graphe planaire restant. Le résultat résulte d'un équilibrage délicat entre la taille des deux niveaux supprimés et le nombre de niveaux qui sont entre eux. Si le plongement du graphe est donné, son séparateur peut être trouvé en temps linéaire. Les graphes de genre $g$ ont également des séparateurs d'arêtes de taille $O({\sqrt {g\Delta n}})$.

Les graphes de genre borné forment un exemple d'une famille de graphes fermés par l'opération de passage aux mineurs, et les théorèmes de séparation s'appliquent également aux familles de graphes fermés par mineurs arbitraires. En particulier, si une famille de graphes a un mineur exclu avec $h$ sommets, alors il a un séparateur avec $O(h{\sqrt {n}})$ sommets, et un tel séparateur peut être trouvé dans le temps $O(n^{1+\varepsilon })$ pour tout $\varepsilon >0$.

La méthode des séparateurs par cercles de Miller et al. (1997) se généralise aux graphes d'intersection de tout système de boules $d$-dimensionnelles avec la propriété que tout point de l'espace est couvert par au plus un certain nombre constant $k$ de boules, aux graphes des $k$-plus proches voisins dans $d$ dimensions et aux graphes issus des maillages éléments finis. Les séparateurs de sphères ainsi construits partitionnent le graphe d'entrée en sous-graphes d'au plus $n(d+1)/(d+2)$ sommets. La taille des séparateurs pour les graphes d'intersection de boules et des graphes des plus proches voisins sont $O(k^{1/d}n^{1-1/d})$ .

Algorithmes « diviser pour régner »

Les décompositions de séparateurs peuvent être utiles pour la conception d' algorithmes de diviser pour régner pour résoudre des problèmes sur des graphes planaires. A titre d'exemple, un problème qui peut être résolu de cette manière est de trouver le cycle le plus court dans un graphe planaire pondéré. Cela peut être fait comme suit :

• Partitionner le graphe donné $G$ en trois sous-ensembles $S$, $A$, $B$ d'après le théorème du séparateur planaire ;
• rechercher récursivement des cycles les plus courts dans $A$ et $B$ ;
• utiliser l'algorithme de Dijkstra pour trouver, pour chaque sommet $s$ dans $S$, le cycle le plus court qui passe par $s$ dans $G$ ;
• renvoyer le plus court des cycles trouvés dans les étapes ci-dessus.

Le temps des deux appels récursifs à $A$ et $B$ dans cet algorithme est dominé par le temps nécessaire pour effectuer les $O({\sqrt {n}})$ appels à l'algorithme de Dijkstra, de sorte que cet algorithme trouve le cycle le plus court dans $O(n^{3/2}\log n)$ temps.

Un algorithme plus rapide pour le même problème de cycle le plus court, exécuté en temps $O(n\log ^{3}n)$, a été donnée par Wulff-Nilsen (2009).

Frederickson a proposé un autre algorithme plus rapide pour trouves les chemins les plus courts depuis une source unique en implémentant le théorème du séparateur dans les graphes planaires. Il s'agit d'une amélioration de l'algorithme de Dijkstra avec une recherche itérative sur un sous-ensemble soigneusement sélectionné des sommets. Cette version prend un temps $O(n{\sqrt {\log n}})$ dans un graphe à $n$ sommets. Henzinger et al. ont étendu la technique de division de Frederickson pour l'algorithme de calcul des chemins les plus courts depuis une source unique dans les graphes planaires à des arêtes de longueurs non négatives et donnent un algorithme en temps linéaire.

La dissection emboîtée est une variation basée sur un séparateur de la technique du diviser pour régner de l'élimination gaussienne dans la résolution des systèmes d'équations linéaires sur une structure de graphe planaire, tels que ceux résultant de la méthode des éléments finis. Il s'agit de trouver un séparateur pour le graphe décrivant le système d'équations, d'éliminer récursivement les variables dans les deux sous-problèmes séparés l'un de l'autre par le séparateur, puis d'éliminer les variables dans le séparateur. Le remplissage du système pour cette méthode (c'est-à-dire le nombre de coefficients non nuls de la décomposition de Cholesky résultante de la matrice) est en $O(n\log n)$, permettant à cette méthode d'être compétitive avec les méthodes itératives pour les mêmes problèmes.

Le paradigme du diviser pour régner qui est basé sur les séparateurs a également été utilisé pour concevoir des structures de données pour les algorithmes sur les graphes dynamiques et la localisation de points, des algorithmes pour la triangulation de polygones des problèmes de plus court chemin ou la construction de graphes voisins les plus proches et des algorithmes d'approximation pour le calcul d'un stable maximal d'un graphe planaire.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Plana separator theorem » (voir la liste des auteurs).

Annexes

Articles connexes

• Séparateur de sommets
• Séparateur géométrique