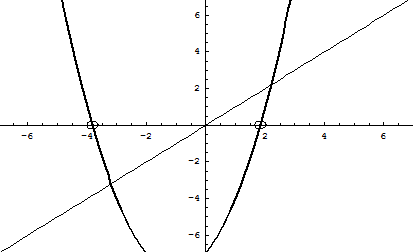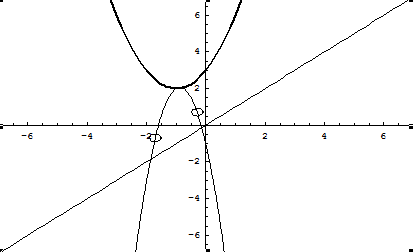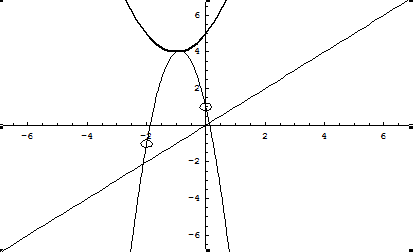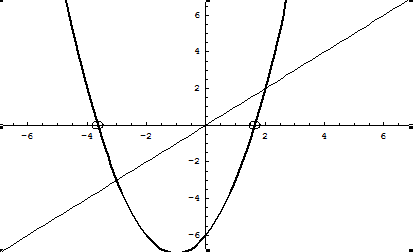Utilisateur:Bdenis/brouillon

Le premier programme (Brouillon)

first try

what about a modern version of the program (from the resurection paper, with the syntax used in the article, and symbolic adress):

«	1 LDN Zero \ (re)set init value for Acc 2 Div: LDN MinusA / with some integer A 3 SUB B \ 4 CMP | loop Acc -= B until Acc <0 (search for rest of Acc/B) 5 JRP Back2 / will exit with Acc = (A % B) - B 6 SUB MinusB \ 7 STO Remainder / compute real Remainder = A % B 8 LDN MinusB \ 9 SUB One | prepare next division : B-- 10 STO B | (set B and MinusB) 11 LDN B | 12 STO MinusB / 13 LDN Remainder \ 14 CMP | test if remainder==0 (if remainder<0, and -remainder<0 then remainder==0) 15 JMP ptrEnd | if yes, then it's finished (Remainder is the greatest proper divisor (-1) of A) 16 JMP ptrDiv | else restart a new division 17 End: STP / 18 Zero: 0 19 MinusA: -262 144 | initial value -A (A any integer) 20 B: 262 143 | initial value : A-1, will change, decreasing 21 Back2: -3 22 MinusB: -262 143 | initial value : -(A-1), will change, increasing 23 ptrDiv: One: 1 | Div-1 24 Remainder: 0 | any initial value, , will change with the remainder A % B 25 ptrEnd: 16 | End-1	»

It's interesting, the 7 instructions of the instruction set are used, even if JMP/JRP could have been expressed with only one of the two forms.

I would need some explanation about line 1, and line 18 (I've seen some explanation, but it didnt convince me), maybe the reason is below (about line 23? but I'm not sure, maybe it's just some kind of a separator between program and data)

A propos, I've been surprised about line 23 (value 1): it is referenced twice with different meanings

• as adress line 16 (for begin of division)
• as value line 9 (for decrement)

As a conclusion line 23 is difficult to translate. It could have been:

«	23 ptrDiv,One: Div-1 | 1 24 Remainder: 0 | any initial value, , will change with the remainder A % B 25 ptrEnd: End-1 | 16	»

(see the coherent change line 25 also)

Maybe, the 'original' should be put side by side to compare and understand the logic.

Second try

maybe something closer to the original (with mnemo from the wikipedia article) without my comments and symbolic adress.

«	1 LDN 18 2 LDN 19 3 SUB 20 4 CMP 5 JRP 21 6 SUB 22 7 STO 24 8 LDN 22 9 SUB 23 10 STO 20 11 LDN 20 12 STO 22 13 LDN 24 14 CMP 15 JMP 25 16 JMP 23 17 STP 18 0 19 -262 144 20 262 143 21 -3 22 -262 143 23 1 24 0 25 16	»

I think

• there is no licence problem
• there is no original work problem (it's just a translation of the 'original program' with the langage used in the wikipedia article, maybe this exists already in some paper)
• the program is really missing in the article
• the question is which form is the best (the first try, or the second, or another [or binary code, or the text from the resurection article]?)

the SSEM's instruction set (only 7 words),  I've added the original notation in the table describing the SSEM's instruction set.

SSEM's instruction set

Binary code	Original notation	Modern mnemonic	Operation
000	S, Cl	JMP S	Jump to the instruction at the adress obtained from the specified memory address S (absolute unconditional jump)
100	Add S, Cl	JRP S	Jump to the instruction at the program counter plus (+) the relative value obtained from the specified memory address S (relative unconditional jump)
010	-S, C	LDN S	Take the number from the specified memory address S, negate it, and load it into the accumulator
110	c, S	STO S	Store the number in the accumulator to the specified memory address S
001 or 101	SUB S	SUB S	Subtract the number at the specified memory address S from the value in accumulator, and store the result in the accumulator
011	Test	CMP	Skip next instruction if the accumulator contains a negative value
111	Stop	STP	Stop

third try

with original comments

«	1 LDN 18 clear accumulator 2 LDN 19 load +a 3 SUB 20 Trial subtraction 4 CMP is difference negative? 5 JRP 21 still positive, Jump back two lines 6 SUB 22 overshot, so add back bn 7 STO 24 store +r n 8 LDN 22 load bn 9 SUB 23 form b(n+1) = bn - 1 10 STO 20 store b(n+1) 11 LDN 20 load -b(n+1) 12 STO 22 store it 13 LDN 24 load -r n 14 CMP is remainder zero? 15 JMP 25 yes, Jump to line 17 16 JMP 23 no, Jump to line 2 17 STP 18 0 19 -262 144 -a 20 262 143 b 21 -3 22 -262 143 -b 23 1 24 0 r 25 16	»

BDenis--90.27.23.74 (talk) 07:59, 18 May 2010 (UTC)

Fourth try

To be sure the third try is the best one, here is a fourth try (and I'll work on a C-Like version, not to compare, but to propose something easier to understand) I don't think a binary version would be better (even if it would be closer to what have really exist)

the program:

«	Original Modern Original notation notation comment 1 -18, C LDN 18 clear accumulator 2 -19, C LDN 19 load +a 3 Sub 20 SUB 20 Trial subtraction 4 Test CMP is difference negative? 5 Add 21, Cl JRP 21 still positive, Jump back two lines 6 SUB 22 SUB 22 overshot, so add back bn 7 c, 24 STO 24 store +r n 8 -22, C LDN 22 load bn 9 SUB 23 SUB 23 form b(n+1) = bn - 1 10 c, 20 STO 20 store b(n+1) 11 -20, C LDN 20 load -b(n+1) 12 c, 22 STO 22 store it 13 -24, C LDN 24 load -r n 14 Test CMP is remainder zero? 15 25, Cl JMP 25 yes, Jump to line 17 16 23, Cl JMP 23 no, Jump to line 2 17 Stop STP load -b(n+1)	»

and the data:

«	18 0 19 -262 144 -a 20 262 143 b 21 -3 22 -262 143 -b 23 1 24 0 r 25 16	»

My preference: probably, the third try. (BDenis)

C Version

«	int minusA = -262144; int B = 262143; int minusB = -262143; int Rem; int Acc; Acc = - 0; do { Acc = - minusA ; do { Acc = Acc - B; } while (Acc>=0); Acc = Acc - minusB; Rem = Acc; Acc = - minusB; Acc = Acc - 1; B = Acc; Acc = - B; minusB = Acc; Acc = - Rem; } while (Acc<0);	»

you can play with it : http://ideone.com/ir0cZ

C Version (second try)

Maybe better ... (even better than asm for modern readers) (the only bad thing : minusA/minusB ... I would like to write -A/-B but it is not legal C idf)

«	int minusA = -262144; int B = 262143; int minusB = -262143; int Rem; int Acc; Acc = - 0; division: Acc = - minusA ; substraction: Acc = Acc - B; if (Acc>=0) goto substraction; Acc = Acc - minusB; Rem = Acc; Acc = - minusB; Acc = Acc - 1; B = Acc; Acc = - B; minusB = Acc; Acc = - Rem; if (Acc>=0) goto end; goto division; end: /* end */	»

you can play with it : http://ideone.com/43PIq

C Version (third try)

with better memory representation for constants and variables.

«	int Zero = 0; int minusA = -262144; int B = 262143; int minusThree = 3; /* for goto substraction */ int minusB = -262143; int One = 1; /* for value 1 and goto division */ int Rem = 0; int Sixteen = 16; /* for goto end */ register int Acc; Acc = - Zero; division: Acc = - minusA ; substraction: Acc = Acc - B; if (Acc>=0) goto substraction; Acc = Acc - minusB; Rem = Acc; Acc = - minusB; Acc = Acc - One; B = Acc; Acc = - B; minusB = Acc; Acc = - Rem; if (Acc>=0) goto end; goto division; end: /* end */	»

Enumération des listes d'entiers

Par application de deux opérateurs : [0|...] et ...+1

[0|...] : ajout d'un élément nul en début d'une liste ...+1 : ajout de un au premier élément d'une liste L'énumération commence avec la liste vide et applique les deux opérateurs tant que possible.

[]

[0]

[0 0] [1]

[0 0 0] [1 0] [0 1] [2]

[0 0 0 0] [1 0 0] [0 1 0] [2 0] [0 0 1] [1 1] [0 2] [3]

Par utilisation d'une borne

Borne max

Une liste est décrite par sa longueur et ses éléments, la borne max d'une liste est le max entre sa longueur et sa plus grande valeur. L'énumération commence avec les listes dont la borne max vaut 0, puis 1, puis 2, ...

[]

[0] [1]

[0 0] [0 1] [0 2] [1 0] [1 1] [1 2] [2] [2 0] [2 1] [2 2]

Borne somme

Une liste est décrite par sa longueur et ses éléments, la borne somme d'une liste est la somme de sa longueur et de ses valeurs. L'énumération commence avec les listes dont la borne somme vaut 0, puis 1, puis 2, ...

[]

[0]

[0 0] [1]

[0 0 0] [0 1] [1 0] [2]

[0 0 0 0] [0 0 1] [0 1 0] [0 2] [1 0 0] [1 1] [2 0] [3]

Non-déterminisme (en informatique)

La notion de non-déterminisme est particulière en informatique : elle renverse le problème du déterminisme, la question n'est pas de savoir si l'avenir est ou n'est pas prévisible, mais de savoir comment prendre en compte l'ensemble des avenirs possibles et aller au delà pour affirmer quelque chose.

Un film peut en donner une idée Smoking / No Smoking de Alain Resnais, qui développe l'ensemble des possibles provenant d'une situation donnée en 2 films, l'un commençant avec un choix positif en faveur d'une cigarette au début du film, l'autre renonçant à cette même cigarette dans les mêmes conditions.

La notion de non-déterminisme apparait en informatique, entre autres, dans la théorie des automates d'état finis (Automate fini), dans le problème "P=NP ?" (Théorie de la complexité des algorithmes) et on la retrouve également en Prolog ou dans l'algorithmique basée sur les points de choix (backtrack).

Automate d'états finis non-déterminisme

Automate NonDéterministe reconnaissant un 1 e n Avant-Avant-Derniere position

(voir Automate fini)

L'approche déterministe semble plus restreinte moins puissante, elle demande de devoir se situer dans une perspective déterministe et refuse d'avoir un doute sur l'avenir. Dans une approche non-déterministe, il semble que l'on gagne en puissance d'expression, car même en l'absence de connaissance de l'avenir l'automate peut prolonger ces calculs en suggérant diverses pistes possibles sans savoir laquelle sera "la bonne". En fait, il s'avère qu'il y a équivalence en matière d'expressivité entre le non-déterminisme et le déterminisme. Ce que saura "calculer" un automate non-déterministe, un automate déterministe pourra aussi le calculer.

Exemple d'automate

L'automate ci-contre présente deux transitions possibles pour 1 sur le début, soit une boucle sur le préfixe, soit une transition en avant vers la fin. Cet automate est donc non-déterministe.

Le langage accepté par cet automate est constitué des mots qui contiennent un 1 en avant-avant-dernière position (un 1 à l'antépénultième position). Lors de la lecture séquentielle d'un caractère, sa position relative par rapport à la fin est inconnue, il se peut que cela soit l'avant-avant-dernier caractère du mot à lire ou pas. Le non-déterminisme utilisé par cet automate propose de considérer ces deux possibilités : c'est l'avant-avant-dernier caractère ou pas.

La théorie des langages formels montre que pour tout langage reconnu par un automate non-déterministe fini, il existe un automate fini déterministe reconnaissant ce même langage.

Dans le cas du langage défini ci-contre, les automates déterministes reconnaissant ce même langage comportent un beaucoup plus grand nombre d'états (la borne du nombre d'états dans le cas général de la détermination d'un automate non-ddéterministe est en 2^n où n est le nombre d'état de l'automate non-déterministe initial), le non-déterminisme introduit une plus grande concision dans l'écriture de l'automate ; cependant, à l'exécution, il n'y a pas nécessairement de gain.

P=NP?

(voir Problème P = NP)

Même si la chose peut sembler lointaine (et bien caché dans l'article Problème P = NP), le N de P=NP signifie Non-déterministe. Il ne faut donc oublier que NP signifie : Non-déterministe Polynomial et non pas Non Polynomial comme une lecture trop rapide ou intuitive pourrait le laisser imaginer.

Dans le cas d'un problème NP, comme la recherche d'une affectation de variables booléennes pour satisfaire un ensemble de contraintes, il y a un ensemble de possibles équivalents sous un certain point de vue (évaluer la valeur de vérité de chaque contrainte) et qui nécessiterait une fonction de choix (un oracle) ou une exploration exhaustive de l'ensemble de ces possibles pour trouver la bonne affectation.

Ce que dit le problème P=NP, c'est que l'exploration de l'ensemble des possibles est incomparablement plus couteux (exponentielle) que d'explorer un possible en particulier (polynomial), mais que cela mis à part, si l'on pouvait explorer cet ensemble de possible comme s'il n'y avait qu'à explorer qu'un seul de ces possible (le bon), le problème serait "raisonnable" (polynomial).

Au passage, le "couteux" de l'exploration combinatoire d'une situation problème donnée rend la mise en œuvre peu réaliste, mais cela ne signifie pas qu'il y a imprédictibilité de la (ré)solution du problème donnée au sens le plus large du terme, entre autres car l'ensemble des possibles est fini, grand mais fini.

Une autre présentation de P=NP consiste à dire qu'il existe une classe de problème pour laquelle la résolution coûte très chère (exponentielle, combinatoire, non polynomiale), alors que la vérification d'une solution proposée par un oracle peut se faire en temps raisonnable (polynomiale). Dans cette présentation, très claire -et c'est l'une de ses grandes qualités- sur la présentation de la différence entre la construction d'une solution et la vérification qu'une proposition est une solution, la notion de non-déterminisme a disparu et malencontreusement, la notion de non polynomiale est apparue, laissant un doute sur le NP de P=NP. Rappelons donc que NP signifie : Non-déterministe Polynomial, et peut-être ainsi la compréhension de la classe de problème NP sera mieux perçue (tout problème non-polynomial n'est pas NP ! bien au contraire, NP concerne des problèmes qui se ressemblent beaucoup plus entre eux que les problèmes non-polynomiaux ne se ressemblent entre-eux, et c'est encore plus vrai pour un sous-classe de problèmes NP que l'on nomme problèmes NP-Complets, où la ressemblance est prouvée)

Non-déterminisme Prolog

En Prolog, le non-déterminisme entraine la possibilité de présenter l'ensemble des réponses possibles à une requête donnée. Ceci repose sur la sémantique de Prolog qui utilise un 'ou' logique à la place de l'alternative ou conditionnelle usuellement utilisée dans les langages de programmation (et qui ressemble plus à un 'ou exclusif' ne laissant pas la place aux deux branches de l'alternative) ou au 'ou bien' qui opère de même.

Exemples d'utilisation du non-déterminisme en Prolog

Quelques idées d'exemples :

• La modélisation des automates d'états finis non-déterminisme est parfois un peu difficile avec les langages de programmation usuel, avec Prolog cela vient naturellement en utilisant la non-déterminisme de Prolog.
• La résolution de problèmes combinatoires (ex : le compte est bon)
• La résolution de problèmes NP

Un exemple explicite, construire P une partie de E :

partie([],[]).
 partie([E|L],P):-partie(L,P).
 partie([E|L],[E|P]):-partie(L,P).

ainsi

?- partie([1,2,3],R).
   R = [];
   R = [3];
   R = [2];
   R = [2, 3];
   R = [1];
   R = [1, 3];
   R = [1, 2];
   R = [1, 2, 3];

Algorithmes de backtrack

(voir Retour sur trace)

Il existe une technique de programmation, non attachée à un langage en particulier, qui développe une approche non-déterministe. C'est la technique du backtrack. Il s'agit de conserver en mémoire les choix effectués lors de la résolution d'un problème et les contextes de la résolution (à l'exécution) lors de ces prises de décision. En cas d'échec final de la résolution, la technique du backtrack consiste à revenir sur ces choix, remettre en cause un à un les choix effectués (en général on commence par le dernier), pour les changer en d'autres décisions et recommencer uen tentative de résolution.

Les techniques de backtrack existent en particulier dans les problèmes de satisfaction de contraintes, les optimisations combinatoires.

Autres points

Opérateur algorithmique

L'algorithmique peut être représentée comme un système fonctionnant à partir de 1+3 opérateurs (l'affectation + 3 structures de contrôles : la séquence, la conditionnelle, la boucle). Parfois un opérateur supplémentaire est ajouté qui introduit la notion de parallélisme. De la même manière, parfois un opérateur supplémentaire est ajouté qui introduit le non-déterminisme. Dans ces deux cas, l'ajout transforme profondément l'algorithmique, plus proche des capacités de la machine mais plus éloigné des formes de raisonnements humains (pour le parallélisme), ou à l'inverse plus proche de formes de raisonnements humains mais plus éloigné des capacités de la machine (pour le non-déterminisme, vu comme le "ou" de la logique classique) ; on comprendra donc que cela ne réussisse pas toujours. L'algorithmique classique (réduite aux structures de controles "simples") est encore la plus répandue.

Non-déterminisme et informatique quantique

En informatique quantique, les problématiques de l'informatique croisent celles de la mécanique quantique. Ainsi, le principe quantique de superposition peut être vu comme analogue au non-déterminisme ou comme une forme de non-déterminisme. Ainsi, l'existence d'algorithmes de recherche quantiques efficaces tirant partie d'éventuels ordinateurs quantiques pourrait éclairer la question P=NP d'un jour nouveau (les experts semblent indiquer cependant qu'il y a peu de chance que cela soit le cas, mais rien n'est encore prouvé.)

Non-déterminisme et déterminisme en informatique

Il y a un paradoxe à parler de non-déterminisme en informatique, car, si l'on excepte quelques domaine de l'informatique comme l'algorithmique probabiliste qui a besoin de hasard et donne des résultats imprévisibles, l'informatique cherche le plus souvent à être déterministe. Le paradoxe, c'est que la notion de non-déterminisme (en informatique, telle que présentée ici) fait partie des concepts de l'informatique dont les mises en œuvre les plus courantes confortent le déterminisme des machines dont se targue en général l'informatique. Ainsi, dans la spécification de Prolog, la résolution Prolog fait appel, à deux moment, à un choix (indeterminé) entre plusieurs propositions (choix d'une clause dans la résolvante, choix d'une règle applicable). Tel que, la résolution prolog serait imprévisible, elle dépendrait des choix. Cependant, dans les mises en œuvre, ces deux choix ont été rendus prévisibles (prendre dans l'ordre). Autre exemple, une approche non-déterministe en automate, est tout à fait déterminé, et déterministe. Relancer deux fois la manip, le résultat sera le même (que ce soit en prolog ou avec un automate) : ouf ! et heureusement pour ces deux formes de programmation ...

Le non-déterminisme en informatique est un déterminisme.

{{Portail|Informatique théorique}} [[Catégorie:Logique mathématique]]

Zéro complexe d'équations réelles (version initiale)

Zéro d'une parabole (cliquer pour voir l'animation)

Rappel principal (cf. théorème de d'Alembert-Gauss) : le degré d'un polynôme $P(X)$ réel est égal au nombre de ses racines (éventuellement) complexes, comptées avec leur multiplicité.

Rappel secondaire (^{[réf. souhaitée]}) : Les racines complexes d'un polynôme réel vont par deux, conjuguées l'une de l'autre.

Autant l'intuition des racines réelles de $P(X)$ est immédiate (ce sont les points de la courbe $Y=P(X)$ qui rencontrent l'axe (ox)), autant l'existence de ces racines complexes peut paraître difficile à acquérir et leur localisation indéterminable intuitivement.

Les complexes, plus généralement, sont des objets mathématiques difficiles à concevoir. Ce fut l'occasion d'une longue lutte entre tenants du réalisme géométrique et formalistes de l'algèbre symbolique (cet article se place du côté du réalisme géométrique).

Une notion proche qui peut être étudiée : les branches réelles de la forme complexe $P(Z)$ (si elles existent), c'est-à-dire, les valeurs complexes, $Z_{i}$, telles que $P(Z_{i})$ est réel. Parmi ces valeurs, on retrouvera les zéros de P.

Degré 0, 1

Les cas des polynômes de degré 0 ou 1 sont sans intérêt : un polynôme constant admet aucune ou une infinité de zéros, un polynôme de degré 1 admet une unique racine réelle.

Degré 2

La courbe réelle $Y=P_{2}(X)$ est une parabole, avec 0 ou 2 zéros réels. Le cas où il n'y a qu'un zéro réel correspond à un zéro réel double.

Lorsqu'il y a 0 zéro réel, les deux zéros sont complexes. Si la parabole n'est pas loin de l'axe, on peut avancer, par un argument de continuité, que les zéros complexes ne sont pas loin de l'optimum, mais au fur et à mesure que la parabole s'éloigne de l'axe, quel est le chemin pris par les zéros complexes ?

Notons $P_{2}(Z)=pZ^{2}+qZ+r$ pour faire quelques calculs.

$P_{2}(X+iY)=(r+qX+pX^{2}-pY^{2})+i(qY+2pXY)$

Si l'on cherche les points réels, il faut annuler le coefficient imaginaire. On trouve $Y=0$, ou $X=-q/2p$. C'est-à-dire la courbe réelle et une courbe dans un plan complexe perpendiculaire à l'axe (ox) au point $-q/2p$ :

$P_{2}(-q/(2p)+iY)=-q^{2}/4p+r-pY^{2}$

Cette courbe est une parabole de direction opposée (-p) à la parabole réelle, qui partage le sommet de cette courbe réelle.

En comptant les zéros de cette courbe et les zéros de la courbe réelle, on trouvera bien 2 zéros, dans tous les cas.

Dans (0x(iy)z), on peut dessiner ces deux courbes pour quelques valeurs de p, q et r par exemple 1, 2 et 3 (en gras la courbe réelle, et il faut imaginer les deux courbes perpendiculaires l'une à l'autre, l'une dans le plan (Oxz), l'autre dans le plan (Oyz)).

et si on anime un peu :

Cette animation illustre également la continuité qu'il existe entre les valeurs des racines et les coefficients de la parabole, que ces racines soient réelles ou complexes et même lorsque l'on se place à l'endroit du passage entre réel et complexe.

Enfin, de ce qui précède, on peut comprendre que le milieu entre les deux racines du polynôme est toujours réel, et se situe au niveau de l'extremum de la parabole. C'est ce type de résultat que l'intuition recherchée ici peut apporter.

Ce résultat s'apparente aux résultats obtenus en géométrie avec l'introduction des complexes, comme par exemple l'existence de l'axe radical entre deux cercles quelle que soit la position relative des deux cercles (cf. Warusfel, qui argumente ainsi "on est conduit ainsi à une géométrie complexifiée où tout est plus simple"). Des résultats qui, s'ils ne sont pas forcément plus simples à saisir, comportent moins de cas particuliers.

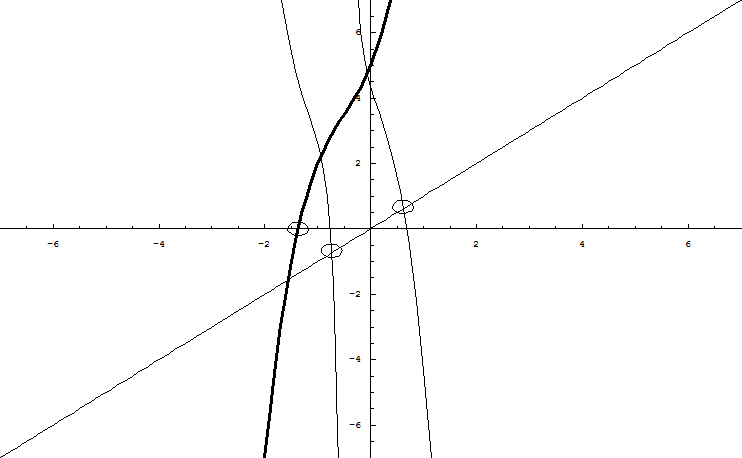
Degré 3

La courbe réelle $Y=P_{3}(X)$ a au moins un zéro réel (éventuellement triple), elle peut en avoir 3, ou 2 (avec 1 double). Si elle n'a qu'un seul zéro réel (simple), alors les deux zéros manquants sont complexes (conjugués l'un de l'autre). Lorsque la courbe réelle de $Y=P_{3}(X)$ possède un coude et que ce coude est proche de l'axe (Ox), alors par un argument de continuité, on peut avancer que les zéros complexes sont proches de cet optimal local, mais quand la courbe ne possède pas de coude, ou que le coude est loin de l'axe (ox), où vont les zéros complexes ?

Notons $P_{3}(Z)=pZ^{3}+qZ^{2}+rZ+s$ pour faire quelques calculs :

$P_{3}(X+iY)=(s+rX+qX^{2}-qY^{2}+pX^{3}-3pXY^{2})+i(rY+2qXY+3pX^{2}Y-pY^{3})$

Si l'on cherche les points réels, il faut annuler le coefficient imaginaire. On trouve Y = 0, ou $Y^{2}=(r+2qX+3pX^{2})/p$. C'est-à-dire la courbe réelle et une courbe complexe symétrique (ce qui assure l'existence de zéros conjugués, si des zéros existent) quand $(r+2qX+3pX^{2})/p$ est positif :

$P_{3}(X+iY//Y^{2}=(r+2qX+3pX^{2})/p)=-qr/p+s-2q^{2}X/p-2rX-8qX^{2}-8pX^{3}$

On retrouve deux courbes de degré 3, orientées dans le sens inverse de la courbe réelle (-8p).

Sur un exemple, avec p, q, r, s égal à 2, 3, 4, 5 (en gras la courbe réelle) :

remarque : ces branches réelles peuvent être discontinues (si $(r+2qX+3pX^{2})/p$ n'est pas positif), il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0 ; et les zéros peuvent 'tomber' dans ces discontinuités. C'est normal, si ces branches existaient toujours, et n'étaient pas discontinues, alors pour $P_{3}$ avec 3 zéros réelles, il faudrait ajouter 2 zéros complexes sur ces branches réelles, ce qui ferait 5 zéros.

Autre voie de recherche : par le passage au quotient

Quand la courbe réelle n'a qu'un zéro réel (strictement), si l'on trace une droite qui passe par ce zéro avec une pente quelconque (par ex. 1), en prenant le quotient de la courbe réelle par cette droite, on obtient une parabole, c'est confirmé par la théorie et la pratique.

D'après ce qui précède, cette parabole a 2 zéros (réels ou complexes), qui sont des zéros réels de la courbe de degré 3. Cela donne les zéros réels, mais pas les éventuelles branches réelles de la courbe complexe. (la branche réelle de la parabole complexe, qui donne les zéros complexes, n'est pas la branche réelle de la forme de degré 3, car il faut (re)multiplier cette courbe par la droite quotient pour revenir à la courbe de degré 3, et on sort alors des réels).

Degré 4

Contrairement au degré 3, il n'y a pas forcément une racine réelle. Toutes les racines peuvent être complexes.

Les résultats pour le degré 4 ressemble à ceux pour le degré 3 : existence de branches réelles sous forme de courbes complexes solution d'équation en $Y^{2}$. Ces courbes sont donc symétriques, et elles peuvent avoir des discontinuités. Les branches sont orientées dans le sens inverse de la courbe réelle.

Contrairement au degré 3, il n'y a pas forcément une racine réelle, il n'y a donc pas de méthode alternative par passage au quotient.

Conclusion

La visualisation des branches réelles pour le degré 2 est intéressante et apporte l'information recherchée : où sont les racines complexes.

La visualisation des branches réelles pour le degré 3, 4 et + -quand elle est possible- n'apporte pas beaucoup, même si elle peut indiquer -quand elle est possible- où sont les racines complexes. La visualisation par la méthode du quotient donne quelques résultats, mais elle n'est pas complètement intuitive (la courbe dérivée est plus intuitive) et ne se généralisera pas aux degrés pairs sans racine réelle.

Les branches réelles ne sont pas toujours définies (il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0).

Articles connexes

• Équation polynomiale
• Théorie des équations (histoire des sciences)
• Théorie des équations (mathématiques)

{{Portail|Mathématiques}} [[Catégorie:Zéro]]

Zéro d'équation réelle devenu Solutions complexes d'équations polynomiales à coefficients réels (version modifiée)

Cas de la parabole (cliquer pour voir l'animation)

Rappel principal (cf. théorème de d'Alembert-Gauss) : le degré d'un polynôme réel $P(X)$ est égal au nombre de ses racines (éventuellement) complexes, comptées avec leur multiplicité.

Autant l'intuition des racines réelles de $P(X)$ est immédiate (ce sont les points dans le plan réel (Oxy) pour lesquels la courbe réelle $Y=P(X)$ rencontrent l'axe (Ox)), autant l'existence et la forme des racines complexes peut paraître difficile à acquérir intuitivement (outre que les racines complexes d'un polynôme réel vont par deux, conjuguées l'une de l'autre).

Les complexes, plus généralement, sont des objets mathématiques difficiles à concevoir. Ce fut l'occasion d'une longue lutte entre tenants du réalisme géométrique et formalistes de l'algèbre symbolique. Cet article se place du côté du réalisme géométrique.

Une notion proche peut être étudiée, ce sont les branches réelles de la forme complexe $P(Z)$, c'est-à-dire, les valeurs complexes $Z=x+iy$ telles que $P(x+iy)$ soit réel, car parmi ces valeurs, on retrouvera les racines de $P$.

Degré 0, 1

Les cas des polynômes de degré 0 ou 1 sont sans intérêt : un polynôme constant admet aucune ou une infinité de racine, un polynôme de degré 1 admet une unique racine réelle.

Degré 2

La courbe réelle $Y=P_{2}(X)$ est une parabole, avec 0 ou 2 intersections avec l'axe des réels. Le cas où il n'y a qu'une seule intersection correspond à une racine réelle double de $P_{2}$.

Lorsqu'il y a 0 intersection avec l'axe des réels, les deux racines de $P_{2}$ sont complexes. Si la parabole n'est pas loin de l'axe, on peut avancer, par un argument de continuité, que les intersections partent dans une dimension complexe, mais ne sont pas loin du sommet de la parabole, mais au fur et à mesure que la parabole s'éloigne de l'axe, quel est le chemin pris par ces intersections complexes ?

Notons $P_{2}(Z)=pZ^{2}+qZ+r$ pour faire quelques calculs.

$P_{2}(X+iY)=(r+qX+pX^{2}-pY^{2})+i(qY+2pXY)$

Si l'on cherche les réels, il faut annuler le coefficient imaginaire. On trouve $Y=0$, ou $X=-q/2p$. C'est-à-dire la courbe réelle et, si l'on se place dans un espace réel à 3 dimensions (2 dimensions pour $Z$ : (Ox) la dimension réelle et (Oy) la dimension portant la valeur imaginaire et enfin une dimension -seulement- pour $P_{2}(Z)$ : (Oz) car nous nous intéressons aux $P_{2}(Z)$ réels), on obtient une courbe dans un plan perpendiculaire à l'axe (Ox) au point $-q/2p$ :

$P_{2}(-q/(2p)+iY)=-q^{2}/4p+r-pY^{2}$

Cette courbe, dans le plan (Oyz), est une parabole de direction opposée $(-p)$ à la parabole réelle du plan (Oxz), qui partage le sommet de cette courbe réelle. Par suite, en comptant les intersections complexes de cette courbe avec (Oxy) et les intersections réelles de la courbe réelle, on trouvera bien les 2 racines de $P_{2}$, dans tous les cas.

Dans (0xyz), on peut dessiner ces deux courbes pour quelques valeurs de p, q et r par exemple 1, 2 et 3 (en gras la courbe réelle, en biais (Oy) l'axe portant la valeur imaginaire de $Z$).

et si on anime un peu :

Cette animation illustre également la continuité qu'il existe entre les valeurs des racines et les coefficients du polynôme, que ces racines soient réelles ou complexes et même lorsque l'on se place à l'endroit du passage entre réel et complexe.

On peut aussi comprendre que les racines des polynômes soient conjuguées, on retrouve également que la somme de ces racines soit un élément caractéristique du polynôme (lié au sommet de la parabole).

Ces intersections complexes s'apparentent à l'axe radical entre deux cercles quelle que soit la position relative des deux cercles (cf. Warusfel, qui argumente ainsi "on est conduit ainsi à une géométrie complexifiée où tout est plus simple").

Degré 3

La courbe réelle $Y=P_{3}(X)$ a au moins une intersection avec l'axe réel (éventuellement triple), elle peut en avoir 3, ou 2 (avec 1 double). Si elle n'a qu'une seule intersection réel (simple), alors les deux intersections manquantes sont complexes (conjuguées l'une de l'autre). Lorsque la courbe réelle de $Y=P_{3}(X)$ possède un coude et que ce coude est proche de l'axe (Ox), alors par un argument de continuité, on peut avancer que les intersections complexes sont proches de cet optimal local, mais quand la courbe ne possède pas de coude, ou que le coude est loin de l'axe (Ox), où vont les intersections complexes ?

Notons $P_{3}(Z)=pZ^{3}+qZ^{2}+rZ+s$ pour faire quelques calculs :

$P_{3}(X+iY)=(s+rX+qX^{2}-qY^{2}+pX^{3}-3pXY^{2})+i(rY+2qXY+3pX^{2}Y-pY^{3})$

Si l'on cherche les points réels, il faut annuler le coefficient imaginaire. On trouve $Y=0$, ou $Y^{2}=(r+2qX+3pX^{2})/p$. C'est-à-dire la courbe réelle et deux courbes complexes symétriques l'une de l'autre (ce qui assure l'existence de racines conjugués, si des racines existent). Quand $Y^{2}=(r+2qX+3pX^{2})/p$ et que cette valeur est positive :

$P_{3}(X+iY)=-qr/p+s-2q^{2}X/p-2rX-8qX^{2}-8pX^{3}$

On retrouve deux courbes de degré 3, orientées dans le sens inverse de la courbe réelle (-8p), avec au moins une intersection avec (Oxy) chacune, ce qui nous donne le nombre de racine de $P_{3}$ recherché.

Sur un exemple, avec p, q, r, s égal à 2, 3, 4, 5 (en gras la courbe réelle, à l'horizontal (Ox) qui porte la partie réelle de $Z$ , en biais l'axe (Oy) qui porte la partie imaginaire de $Z$, n.b. les intersections imaginaires avec (Oxy) sont proches de (Oy) dans cet exemple mais ne sont pas sur (Oy)) :

remarque : l'existence de ces branches réelles n'est pas assurée (il faut que $(r+2qX+3pX^{2})/p$ soit positif). Il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0 et les intersections avec (Oxy) peuvent ainsi disparaitre. C'est normal, si ces branches existaient toujours alors pour $P_{3}$ avec 3 intersections réelles, il faudrait ajouter 2 intersections complexes sur ces branches réelles, ce qui ferait 5 racines en tout pour $P_{3}$.

Degré 4

Contrairement au degré 3, il n'y a pas forcément une racine réelle. Toutes les racines peuvent être complexes.

Les résultats pour le degré 4 ressemble à ceux pour le degré 3 : existence de branches réelles sous forme de courbes complexes solution d'équation en $Y^{2}$. Ces courbes sont donc symétriques, et elles peuvent avoir des discontinuités. Les branches sont orientées dans le sens inverse de la courbe réelle.

Contrairement au degré 3, il n'y a pas forcément une racine réelle, il n'y a donc pas de méthode alternative par passage au quotient.

Conclusion

La visualisation des branches réelles pour le degré 2 est intéressante et apporte l'information recherchée : où sont les racines complexes.

La visualisation des branches réelles pour le degré 3, 4 et + -quand elle est possible- n'apporte pas beaucoup, même si elle peut indiquer -quand elle est possible- où sont les racines complexes. La visualisation par la méthode du quotient donne quelques résultats, mais elle n'est pas complètement intuitive (la courbe dérivée est plus intuitive) et ne se généralisera pas aux degrés pairs sans racine réelle.

Les branches réelles ne sont pas toujours définies (il suffit de prendre r et p de signe opposé dans la forme de degré 3 pour que la branche réelle disparaisse autour de X=0).

Articles connexes

• Équation polynomiale
• Théorie des équations (histoire des sciences)
• Théorie des équations (mathématiques)

{{Portail|Mathématiques}} [[Catégorie:Zéro]]

Récursivité structurelle

L'article original a disparu, supprimé par WP pendant l'été 2016, à tort à mon avis, pour ne pas avoir compris le sujet de l'article ... Cet article montrait avec de nombreux exemples différents algorithmes ou formes d'algorithmes basés sur l'analyse récursive des listes : qlq schémas de récursion, et pas particulièrement map, reduce, mais plutôt hors map, reduce, i.e. les schémas "atypiques", ex. : ceux où le cas de base n'est pas la liste vide, ou n'est pas unique, ou la propagation prends deux éléments et pas un seulement, etc. les cas "tordus" diraient certains ; les cas réels je pense plutôt, car dans la réalité, les cas qui arrivent ne sont pas toujours les plus simples ...

L'article original a disparu, mais l'idée reste.

la suite est en ProLog. Rappelons simplement que la liste vide en ProLog s'écrit : [], les listes en extension : [1,2,3] et les listes en intension sont définies par leur premier élément et leur queue (liste elle-même) : [E|Q].

Schéma de récursion habituel sur les listes

Généralement, les exercices consistent à définir un algorithme en appliquant une analyse récursive basée sur la structure récursive d'une liste. Le schéma de base du programme est donc :

• prog(cas_de_base).
• prog([E|Q]) :- prog(Q).

et souvent le cas de base concerne la liste vide [ ]

Exemple, calcul de la longueur d'une liste

• longueur(0,[]).
• longueur(N+1,[E|Q]) :- longueur(N,Q).

Pour préciser, on a ici⁽⁰⁾ un cas de base unique^(-1), avec []^(-2) et un cas de propagation unique^(-3), sur [E|Q](-4), consommant un seul élément^(-5) E^(-6) et engendrant un seul appel récursif^(-7) sur Q^(-8) pour mettre en œuvre une récurrences unique^(-9).

(on pourrait ajouter, qu'ici la récurrence structurelle porte sur le second argument, qu'il y a un calcul supplémentaire effectué en parallèle [sur le premier argument], que le cas vide correspond sur à 0 [l'élément neutre de l'opération "+" effectuée dans la propagation], etc ... et imaginer d'autres variantes encore)

9 autres schémas de récursion

Cas de base unique non vide (cf. 2)

Parfois le cas de base comporte un élément, ou un nombre précis d'éléments, parfois le cas de base est plus général.

Exemple, avec 1 élément : vérifier qu'une liste est de longueur impair.

• longueurImpaire([E]).
• longueurImpaire([E,F|Q]) :- longueurImpaire(Q).

Exemple, avec plus d'un élément (sans avoir un nombre d'élément précis) : vérifier que 0 apparait dans une liste

• avecZero([0|Q]).
• avecZero([E|Q]) :- avecZero(Q).

Cas de base multiple (cf. 1)

Parfois un cas de base ne suffit pas, il en faut deux ou plus (mais un nombre précis).

Exemple, avec 2 cas de base : calcul de la parité de la longueur d'une liste.

• paritéLongueur([],pair).
• paritéLongueur([E],impair).
• paritéLongueur([E,F|Q],Parité) :- paritéLongueur(Q,Parité).

Cas de propagation unique avec plus d'un élément (cf. 3)

Parfois la connaissance d'un seul élément en tête de liste ne suffit pas, il en faut plus.

n.b. : pour assurer la complétude du programme, en général, il y aura aussi plusieurs cas de base.

Exemple, avec 2 éléments en tête de liste pour la propagation : vérifier qu'une liste est constante.

• listeConstante([]).
• listeConstante([E]).
• listeConstante([E,E|Q]) :- listeConstante([E|Q]).

Cas de propagation multiple avec plus d'un élément

Parfois un cas de propagation ne suffit pas, il en faut deux ou plus (mais un nombre précis). C'est souvent le cas, quand il faut gérer un si-alors-sinon.

Exemple avec 2 cas de propagation : suppression de toutes les occurences de 0 dans une liste.

• sansZero([],[]).
• sansZero([0|Q],R) :- sansZero(Q,R).
• sansZero([E|Q],[E|R]) :- dif(E,0), sansZero(Q,R).

Consommation de plus d'un élément (cf. 5)

Parfois la propagation consomme plus d'un élément. C'est un sous cas de la propagation avec plus d'un élément, et comme pour la propagation avec plus d'un élément, pour assurer la complétude du programme, en général, il y aura aussi plusieurs cas de base.

Exemple avec consommation de 2 éléments : vérifier qu'aux rangs pairs on a un entier pair et aux rangs impairs un entier impair.

• rangParité([]).
• rangParité([E]) :- pair(E).
• rangParité([E,F|Q]) :- pair(E), impair(F), rangParité(Q).

Propagation avec plusieurs appels récursifs (cf. 4, 7, 8)

Parfois le(s) cas de propagation ont besoin de plus d'un appel récursif.

Exemple avec 2 appels récursif dans la propagation : tri fusion.

• triFusion([],[]).
• triFusion(L,T):- coupe(L,L1,L2), triFusion(L1,T1), triFusion(L2,T2), fusion(T1,T2,T).

Récurrence multiple (cf. 6, 9)

Parfois plusieurs récurrences coexistent.

Exemple avec 2 récurrences : la fusion de deux listes triées.

• fusion([],L,L).
• fusion([E|Q],[],[E|Q]).
• fusion([E|Q],[F|R],[M|S]):- minMax(E,F,M,N), fusion([N|Q],R,S).

Preuve par l'exemple

Une preuve par l'exemple (resp. la recherche de contre-exemple) est une forme de démonstration permettant de valider (resp. invalider) une proposition à l'aide d'exemples. Un exemple permet de démontrer un énoncé existentiel (il existe un objet ayant une certaine propriété), un contre-exemple d'invalider un énoncé universel (tous les objets considérés ont une certaine propriété). Dans certains cas particulier, et après un travail préalable, il est possible de démontrer une propriété pour un nombre infini d'objets à l'aide d'un nombre fini d'exemples.

Remarque : dans les titres qui suivent, le terme 'un cas' pourrait être remplacé par 'un exemple' si cela ne portait pas à confusion

Un cas de preuve par l'exemple d'une propriété existentielle

A démontrer : il existe des entiers multiples de 2 et 3.

Preuve par 2 exemples : il suffit de prendre n=6, n=12.

Un cas de contre-exemple pour une propriété universelle

A réfuter : pour tout entier n, n est multiple de 2 et 3.

Contre-exemple : il suffit de prendre n=5.

Un cas de preuve par l'exemple d'une propriété universelle

Le travail à produire est plus important.

A démontrer : pour tout entier n, $(n+1)^{2}$ est égal à $n^{2}+2n+1$

Preuve par 3 exemples : si l'on regarde la différence $(n+1)^{2}-(n^{2}+2n+1)$, il suffit de prouver que cette différence est toujours nulle. Sans faire les calculs, cette expression peut être assimilée à une forme polynomiale en n de degré 2 maximum^{[réf. nécessaire]}. Si elle est de degré 2 ou de degré 1, elle n'a que 2 ou 1 zéros. Or pour n=0, n=1, n=2 (3 exemples pris au hasard, l'important c'est d'avoir un exemple de plus que le degré maximum supposé), $(n+1)^{2}-(n^{2}+2n+1)$ vaut zéro, cette forme polynomiale ne peut donc être de degré 2 ou 1, elle est donc de degré 0, et sa valeur est constante, elle vaut donc 0, donc $(n+1)^{2}-(n^{2}+2n+1)$ est identiquement nul. CQFD.

Remarque : une preuve un peu plus poussée, en utilisant la méthode proposée par Hong, permet de n'utiliser qu'un seul exemple, pour cela il faut raisonner sur les valeurs possibles des coefficients de $(n+1)^{2}-(n^{2}+2n+1)$ -en supposant que ce n'est pas le polynôme nul- et en déduire le rayon de la sphère où se trouvent les zéros. Alors, en prenant un exemple numérique hors de cette sphère, si la valeur de cette forme polynomiale est égale à 0, c'est que la forme polynomiale est identiquement nulle.

Voir aussi

• Exemple
• Exemple (mathématiques)
• Contre-exemple

Section suivante

pour la suite ...