Utilisateur:RudeWolf/traduction/topologie

La topologie (Du Grec topos, pour « lieu », et logos, « discours ») est la branche des mathématiques qui étudie les propriétés de l'espace qui sont préservées sous l'action de transformations continues. La topologie est née de la géométrie, mais à la différence de celle-ci, la topologie ne traite pas des concepts de nature métrique, comme la distance entre deux points. La topologie s'occupe plutôt des propriétés qui témoignent de comment un espace est constitué, comme sa connexité ou son orientabilité.

Le mot topologie s'utilise à la fois pour désigner une discipline, mais aussi une famille de partie d'un espace satisfaisant certaines propriétés. Une telle famille est en effet l'objet le plus fondamental en topologie: c'est elle qui définit la structure « d'espace topologique ». Une classe importante de transformations qui interviennent en topologie est celle des homéomorphismes (du grec homeo, semblable, et du grec pour « forme »). De façon imagée, on se représente ces transformations par l'action consistant à étirer un objet élastique sans le disloquer ni provoquer de déchirure. Une autre notion importante de transformation est couverte par le concept d'homotopie.

Les fondateurs de la discpline utilisaient à l'origine le nom de geometria situs ou analysis situs ( du latin situs, pour « lieu »). Depuis 1925 jusque 1975, cette discipline fut d'importance grandissante au sein des mathématiques. Aujourd'hui la topologie est une vaste branche des mathématiques comprenant des champs variés. L'énoncé de la conjecture de Poincaré, l'un des sept problèmes Clay, relève exclusivement de la topologie. Les divise traditionnellement la topologie en topologie générale, qui étudie certains concept fondamentaux comme la compacité, la connexité; la topologie algébrique, qui se sert d'outils comme le groupe fondamental, l'algèbre d'homologique; la topologie géométrique, qui s'intéresse principalement aux variétés et à leur plongements dans d'autres variétés. Certains des domaines les plus dynamiques de la topologie, comme la topologie en basse dimension, sont transversaux à cette division.

See also: topologie glossary for definitions of some of the terms used in topologie and topological space for a more technical treatment of the subject.

History modifier

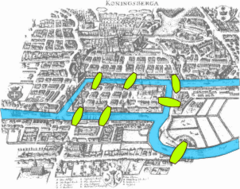
The branch of mathematics now called topologie began with the investigation of certain questions in geometry. Euler's 1736 paper on Seven Bridges of Königsberg is regarded as one of the first topological results.

The term "Topologie" was introduced in German in 1847 by Johann Benedict Listing in Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen, pp. 67, 1848. However, Listing had already used the word for ten years in correspondence. "la topologie," its English form, was introduced in 1883 in the journal Nature to distinguish "qualitative geometry from the ordinary geometry in which quantitative relations chiefly are treated". The term topologist in the sense of a specialist in topologie was used in 1905 in the magazine Spectator.

Modern topologie depends strongly on the ideas of set theory, developed by Georg Cantor in the later part of the 19th century. Cantor, in addition to setting down the basic ideas of set theory, considered point sets in Euclidean space, as part of his study of Fourier series.

Henri Poincaré published Analysis Situs in 1895, introducing the concepts of homotopy and homology, which are now considered part of algebraic topologie.

Maurice Fréchet, unifying the work on function spaces of Cantor, Volterra, Arzelà, Hadamard, Ascoli and others, introduced the metric space in 1906. A metric space is now considered a special case of a general topological space. In 1914, Felix Hausdorff coined the term "topological space" and gave the definition for what is now called a Hausdorff space. In current usage, a topological space is a slight generalization of Hausdorff spaces, given in 1922 by Kazimierz Kuratowski.

For further developments, see point-set topologie and algebraic topologie.

Elementary introduction modifier

A continuous deformation (homotopy) of a coffee cup into a doughnut (torus) and back.

Topological spaces show up naturally in almost every branch of mathematics. This has made topologie one of the great unifying ideas of mathematics.

The motivating insight behind topologie is that some geometric problems depend not on the exact shape of the objects involved, but rather on the way they are put together. For example, the square and the circle have many properties in common: they are both one dimensional objects (from a topological point of view) and both separate the plane into two parts, the part inside and the part outside.

One of the first papers in topologie was the demonstration, by Leonhard Euler, that it was impossible to find a route through the town of Königsberg (now Kaliningrad) that would cross each of its seven bridges exactly once. This result did not depend on the lengths of the bridges, nor on their distance from one another, but only on connectivity properties: which bridges are connected to which islands or riverbanks. This problem, the Seven Bridges of Königsberg, is now a famous problem in introductory mathematics, and led to the branch of mathematics known as graph theory.

Similarly, the hairy ball theorem of algebraic topologie says that "one cannot comb the hair flat on a hairy ball without creating a cowlick." This fact is immediately convincing to most people, even though they might not recognize the more formal statement of the theorem, that there is no nonvanishing continuous tangent vector field on the sphère. As with the Bridges of Königsberg, the result does not depend on the exact shape of the sphere; it applies to pear shapes and in fact any kind of smooth blob, as long as it has no holes.

In order to deal with these problems that do not rely on the exact shape of the objects, one must be clear about just what properties these problems do rely on. From this need arises the notion of homeomorphism. The impossibility of crossing each bridge just once applies to any arrangement of bridges homeomorphic to those in Königsberg, and the hairy ball theorem applies to any space homeomorphic to a sphere.

Intuitively, two spaces are homeomorphic if one can be deformed into the other without cutting or gluing. A traditional joke is that a topologist can't distinguish a coffee mug from a doughnut, since a sufficiently pliable doughnut could be reshaped to the form of a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.

Homeomorphism can be considered the most basic topological equivalence. Another is homotopy equivalence. This is harder to describe without getting technical, but the essential notion is that two objects X and Y are homotopy equivalent if there is an object Z such that Z contains both X and Y and Z can be "squished" down in different ways to X and Y. A particularly simple case is when we can take Z to be one of X and Y, let's say X. In this case, Y can be put in X and then X can be squished down to Y.

Equivalence classes of the English alphabet in uppercase sans-serif font (Myriad); left - homeomorphism, right - homotopy equivalence

An introductory exercise is to classify the uppercase letters of the English alphabet according to homeomorphism and homotopy equivalence. The result depends partially on the font used. The figures use a sans-serif font named Myriad. Notice that homotopy equivalence is a rougher relationship than homeomorphism; a homotopy equivalence class can contain several of the homeomorphism classes. The simple case of homotopy equivalence described above can be used here to show two letters are homotopy equivalent, e.g. O fits inside P and the tail of the P can be squished to the "hole" part.

To be sure we have classified the letters correctly, we not only need to show that two letters in the same class are equivalent, but that two letters in different classes are not equivalent. In the case of homeomorphism, this can be done by suitably selecting points and showing their removal disconnects the letters differently. For example, X and Y are not homeomorphic because removing the center point of the X leaves four pieces; whatever point in Y corresponds to this point, its removal can leave at most three pieces. The case of homotopy equivalence is harder and requires a more elaborate argument showing an algebraic invariant, such as the fundamental group, is different on the supposedly differing classes.

Letter topologie has some practical relevance in stencil typography. The font Braggadocio, for instance, has stencils that are made of one connected piece of material.

Mathematical definition modifier

Article principal : Topological space.

Let X be any set and let T be a family of subsets of X. Then T is a topologie on X if

Both the empty set and X are elements of T.
Any union of arbitrarily many elements of T is an element of T.
Any intersection of finitely many elements of T is an element of T.

If T is a topologie on X, then X together with T is called a topological space.

All sets in T are called open; note that in general not all subsets of X need be in T. A subset of X is said to be closed if its complement is in T (i.e., it is open). A subset of X may be open, closed, both, or neither.

A function or map from one topological space to another is called continuous if the inverse image of any open set is open. If the function maps the real numbers to the real numbers (both space with the Standard la topologie), then this definition of continuous is equivalent to the definition of continuous in calculus. If a continuous function is one-to-one and onto and if the inverse of the function is also continuous, then the function is called a homeomorphism and the domain of the function is said to be homeomorphic to the range. Another way of saying this is that the function has a natural extension to the topologie. If two spaces are homeomorphic, they have identical topological properties, and are considered to be topologically the same. The cube and the sphere are homeomorphic, as are the coffee cup and the doughnut. But the circle is not homeomorphic to the doughnut.

la topologie topics modifier

Some theorems in general topologie modifier

Every closed interval in R of finite length is compact. More is true: In Rⁿ, a set is compact if and only if it is closed and bounded. (See Heine-Borel theorem).
Every continuous image of a compact space is compact.
Tychonoff's theorem: The (arbitrary) product of compact spaces is compact.
A compact subspace of a Hausdorff space is closed.
Every continuous bijection from a compact space to a Hausdorff space is necessarily a homeomorphism.
Every sequence of points in a compact metric space has a convergent subsequence.
Every interval in R is connected.
Every compact m-manifold can be embedded in some Euclidean space Rⁿ.
The continuous image of a connected space is connected.
A metric space is Hausdorff, also normal and paracompact.
The metrization theorems provide necessary and sufficient conditions for a topologie to come from a metric.
The Tietze extension theorem: In a normal space, every continuous real-valued function defined on a closed subspace can be extended to a continuous map defined on the whole space.
Any open subspace of a Baire space is itself a Baire space.
The Baire category theorem: If X is a complete metric space or a locally compact Hausdorff space, then the interior of every union of countably many nowhere dense sets is empty.
On a paracompact Hausdorff space every open cover admits a partition of unity subordinate to the cover.
Every path-connected, locally path-connected and semi-locally simply connected space has a universal cover.

General topologie also has some surprising connections to other areas of mathematics. For example:

in number theory, Furstenberg's proof of the infinitude of primes.

Some useful notions from algebraic topologie modifier

Homology and cohomology: Betti numbers, Euler characteristic, degree of a continuous mapping.
Intuitively-attractive applications: Brouwer fixed-point theorem, Hairy ball theorem, Borsuk-Ulam theorem, Ham sandwich theorem.
Homotopy groups (including the fundamental group).
Chern classes, Stiefel-Whitney classes, Pontryagin classes.

Generalizations modifier

Occasionally, one needs to use the tools of topologie but a "set of points" is not available. In pointless topologie one considers instead the lattice of open sets as the basic notion of the theory, while Grothendieck topologies are certain structures defined on arbitrary categories which allow the definition of sheaves on those categories, and with that the definition of quite general cohomology theories.