Utilisateur:VincentPalmieri/topologie

La topologie (du grec topos, lieu, et logos, étude) est une branche des mathématiques s'intéressant aux propriétés spatiales conservées par déformations bicontinues (étirer sans déchirer ni coller) ; on les appelle invariants topologiques. !!! When the discipline was first properly founded, in the early years of the 20th century, it was still called geometria situs ([du [latin]] géométrie de position) and analysis situs (du latin analyse de position). De 1925 à 1975 environ, c'est la branche des mathématiques qui a connu la plus importante croissance.
La topologie désigne également un objet mathématique particulier étudié dans ce domaine. Dans ce sens, une topologie est une famille d'ouverts qui contient l'ensemble vide et l'espace entier. Si une famille d'ensembles est dans la topologie, alors son union doit s'y trouver également. Si un nombre fini d'ensembles est dans la topologie, alors son intersection doit également y être. Un ensemble équipé d'une topologie est appelé espace topologique. Le reste de cet article concerne la branche des mathématiques appelée topologie.
La topologie est parfois appelée géométrie de la feuille de caoutchouc parce qu'elle ne distingue pas un cercle d'un carré (un cercle découpé dans un morceau de caoutchouc peut être étiré en un carré), mais fait la différence entre un cercle et le tracé du chiffre huit (on ne peut pas étirer le chiffre huit en un cercle sans le "déchirer"). Les espaces étudiés en topologie sont appelés espaces topologiques. Ils peuvent varier des classiques variétés à certaines constructions très exotiques.
La topologie a introduit un nouveau langage géométrique (Complexe simplicial, cohomologie, dualité de Poincaré, fibration, Fibré vectoriel, Faisceau, classe caractéristique, fonction de Morse, algèbre homologique, Suite spectrale). Elle a eu un impact majeur sur les champs de la géométrie différentielle, la géométrie algébrique, les systèmes dynamiques, les équation aux dérivées partielles, et la théorie des fonctions de plusieurs variables complexes. La géométrie, au sens de Michael Atiyah et son école, inclut maintenant tout cela. Dans le sujet-même, !!!la point-set topology ou topologie générale est l'étude des espaces topologiques sans davantage de restrictions ; d'autres domaines traitent des espaces topologiques qui ressemble davantage aux variétés. Cela inclut l'algèbre topologique (qui s'est développée à partir de la topologie combinatoire), la topologie géométrique, la topologie des petites dimensions, traitant par exemple de la théorie des nœuds, et la topologie différentielle. Cet article donne un aperçu général de la topologie. Pour des définitions mathématiques plus précises, consulter l'un des articles plus spécialisés cités ci-dessous. Le glossaire topologique contient les définitions de termes utilisés dans ce domaine.
Histoire
modifier
L’origine de la topologie est l’étude de la géométrie dans les cultures antiques. Le travail de Leonhard Euler datant de 1736 sur le problème des sept ponts de Königsberg est considéré comme l’un des premiers résultats de géométrie qui ne dépend d’aucune mesure, c’est-à-dire l’un des premiers résultats topologiques.
Georg Cantor, l'inventeur de la théorie des nombres, commença à étudier la théorie des ensembles de points dans un espace euclidien durant la seconde moitié du XIXe siècle.
/!\(Cette ligne a été supprimée de l'article actuel ; voir le commentaire de Maks) /!\
Henri Poincaré publia Analysis Situs en 1895, introduisant les concepts d'homotopie et d'homologie.
Maurice Fréchet, unifiant les travaux sur les espaces de fonctions de Cantor, Volterra, Arzelà, Hadamard, Ascoli et d’autres, introduit le concept d'espace métrique en 1906.
En 1914, Felix Hausdorff, en généralisant la notion d’espace métrique, inventa le terme d'« espace topologique » et définit ce qui s'appelle aujourd'hui l'espace de Hausdorff.
Finalement, une autre légère généralisation en 1922, par Kuratowski, donna le concept actuel d'espace topologique.
Le terme « topologie », fut introduit en allemand en 1847 par Johann Benedict Listing dans « Vorstudien zur Topologie ».
le terme "topologie" fut introduit en Allemagne en 1847 par Johann Benedict Listing dans Vorstudien zur Topologie, Vandenhoeck und Ruprecht, Göttingen, pp. 67, 1848. Cependant, Listing avit déjà employé ce mot pendant dix ans dans ses correspondances. Je passe la partie concernant l'année du terme dans la langue anglaise.
Petite introduction
modifierLes espaces topologiques apparaissent naturellement en analyse (mathématiques), en algèbre abstraite et en géométrie. Cela a fait de la topologie l'une des grandes idées unificatrices des mathématiques. La topologie générale, !!! or point-set topology, définit et étudie quelques propriétés utiles des espaces et des fonctions continues, telles que la connectivité, la compacité et la continuité. La topologie algébrique est un outil puissant pour étudier les espaces topologiques, et les fonctions continues entre elles. !!! It associates "discrete", more computable invariants to maps and spaces, souvent d'une manière fonctorielle. Les idées développées en algèbre topologique on une une forte influence sur l'algèbre et la géométrie algébrique.
!!!The motivating insight behind la topologie est que certains problèmes géométriques ne dépendent pas de la forme exacte des objets impliqués, mais plutôt de "manière de laquelle ils sont connectés les uns aux autres". L'une des premières études de topologie a été la démonstration par Leonhard Euler qu'il était impossible de trouver une route à travers la route de Königsberg (aujourd'hui Kaliningrad) qui traverse chacun de ses sept ponts une fois et une seule. Ce résulta ne dépendait pas de la longueur des ponts, ni de leurs distances les uns aux autres, mais seulement de leur connectivité : quels ponts sont connectés à quelle île ou rive. Ce problème, le problème des sept ponts de Königsberg, est aujourd'hui un célèbre problème d'introduction aux mathématiques, et a mené à la branche des mathématiques appelée théorie des graphes.
De la même manière le théorème de la boule chevelue, en topologie algébrique, affirme que l"'on ne peut pas bien peigner une boule chevelue". La proposition est immédiatement admise par la plupart des gens, même s'il ne seraient pas capables de comprendre l'écriture formelle du théorème : !!!there is no nonvanishing continuous tangent vector field on the sphère. Tout comme pour les ponts de Königsberg, le résultat ne dépend pas de la forme exacte de la sphère ; il s'applique aux formes en poire, et de manière générale à toutes sortes de formes (sous certaines conditions concernant la régularité de la surface), tant qu'elles n'ont pas de trous.
Pour pouvoir traiter ces problèmes qui ne reposent pas sur la forme exacte des objets, il faut précisément être clair sur les propriétés dont ils dépendent. C'est pour répondre à ce besoin qu'est apparue la notion d'équivalence topologique. L'impossibilité de traverser chaque pont une seule fois s'applique à n'importe quel arrangement de ponts topologiquement équivalents à ceux de Königsberg, et le théorème de la boule chevelue s'applique à n'importe quel espace topologiquement équivalent à une sphère. Formellement, deux espaces sont topologiquement équivalents s'il existe un homéomorphisme entre eux. Dans ce cas ces deux espaces sont dits homéomorphiques, et ils sont considérés comme étant exactement les mêmes dans le cadre de la topologie.
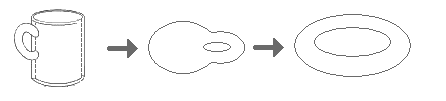
Formellement, un homéomorphisme est défini comme bijection continue avec une réciproque continue, ce qui n'est pas très intuitif, même pour ceux qui connaissent le sens des termes de la définition. Un critère plus informel en donne une meilleure perception visuelle : deux espaces sont topologiquement équivalents si l'un peut être déformé en l'autre sans le découper ou en coller des morceaux ensembles. Une plaisanterie traditionnelle raconte qu'une topologiste ne peut pas faire la différence entre le café qu'elle boit et le donut qu'elle mange, vu qu'un donut suffisamment souple peut être déformé en une tasse de café en y créant une cuvette et en l'élargissant progressivement, tout en rétrécissant le trou pour en faire une poignée.
Un exercice introductif simple consiste à classifier les lettres minuscules de l'alphabet français suivant leur équivalence topologique. Pour faire simple, on suppose que les traits des lettres ont une largeur non nulle. Ainsi, dans la plupart des polices modernes utilisées, on trouve la classe {a,b,d,e,o,p,q} des lettres avec un trou, la classe {c,f,h,k,l,m,n,r,s,t,u,v,w,x,y,z} des lettres sans trou, et la classe {i,j} des lettres constituées de deux morceaux. g peut aussi bien appartenir à la classe avec un trou ou être le seul élément de la classe des lettres à deux trous, selon que sa queue est fermée ou non. Pour un excercice plus complexe, on peut supposer que les lignes ont une largeur nulle ; on peut alors obtenir différentes classifications suivant la police utilisée. La topologie des lettres trouve un intérêt pratique dans la typographie de pochoir : la police Braggadocio, par exemple, peut être taillée dans une surface sans que des morceaux tombent sans qu'on le veuille.
Quelques théorèmes de topologie générale
modifier- Tout intervalle fermé de R de longueur finie est compact. De plus, dans Rn, un ensemble est compact si et seulement si il est fermé et borné. (voir : Théorème de Borel-Lebesgue)
- Toute image continue d'un espace compact est compact.
- Théorème de Tychonov : Le produit (arbitraire) d'un ensemble d'espaces compacts est compact.
- Un sous-espace compact d'un espace de Hausdorff est fermé.
- Toute suite de points d'un espace métrique compact contient une sous-suite convergente.
- Tout intervalle de R est connexe.
- L'image continue d'un espace connexe est connexe.
- Un espace métrique est de Hausdorff, et également normal et paracompact.
- Les théorèmes de métrisation donnent les conditions nécessaires et suffisantes à une topologie !!!to come from a metric.
- Le théorème de prolongement de Tietze : Dans un espace normal, toute fonction continue à valeur réelle définie sur un sous-espace fermé peut être étendue à une fonction continue définie sur tout l'espace.
- Le théorème de catégorie de Baire : Si X est un espace métrique complet ou un espace de Hausdorff localement compact alors l'intérieur de toute union dénombrable d'ensembles nulle part denses.
- Dans un espace de Hausdorff paracompact !!!every open cover admits a partition d'unité subordinate to the cover.
- Every path-connected, locally path-connected and semi-locally simply connected space has a universal cover.
- Les espaces topologiques ont une dimension topologique
Quelques notions utiles d'algèbre topologique
modifier- Homologie et cohomologie : nombres de Betti, Caractéristique d'Euler.
- Applications intuitivement intéressantes : Théorème du point fixe de Brouwer, Théorème de Borsuk-Ulam, Théorème du sandwich au jambon.
- groupes d'homotopie (incluant le groupe fondamental).
- Classes de Chern, classes de Stiefel–Whitney, classes de Pontryagin.
!!!Outline of the deeper theory
modifier- (Co)fibre sequences: Puppe sequence, computations
- Homotopy groups of spheres
- Obstruction theory
- K-theory: KO-theory, algebraic K-theory
- Stable homotopy theory
- Brown's representability theorem
- (Co)bordism
- Signatures
- Brown-Peterson BP and Morava K-theory
- Surgery obstructions
- H-spaces, infinite loop spaces, A∞ rings
- Homotopy theory of affine schemes
- Intersection cohomology
Généralisations
modifierOccasionnellement, on a besoin d'utiliser les outils de la topologie mais un "ensemble de points" n'est pas disponible. En topologie sans points, on considère à la place le treillis des ensembles ouverts comme notion de base de la théorie, tandis que les topologie de Grothendieck sont des structures définies sur des catégories arbitraires qui permettent la définition de faisceaux sur ces catégories, et ainsi la définition de théories de cohomologie assez générales.
Topologie en psychanalyse
modifierLa topologie a influencé la psychanalyse depuis son emploi par Jacques Lacan à partir 1962, où elle est utilisée comme langage de description des structures psychiques. Par exemple, selon la psychanalyse lacanienne, la relation entre le Réel, l'Imaginaire et le Symbolique est homéomorphe à un anneau borroméen. Historiquement, ces formalisations de la psychanalyse peuvent être attribuées à l'influence des mathématiques structurales parisiennes, avec par exemple Nicolas Bourbaki. Cependant, l'usage que fait Lacan de la topologie, comme son utilisation de l'algèbre, ne respecte pas les standards de rigueur normalement attendus par la discipline mathématique, et devrait davantage être considéré comme une analogie (la valeur de laquelle étant laissée au jugement du lecteur) qu'une branche des mathématiques appliquées.