Empilement de cercles dans un triangle équilatéral
L'empilement de cercles dans un triangle équilatéral est un problème d'empilement bidimensionnel dont l'objectif est d'empiler des cercles unités identiques de nombre n dans le triangle équilatéral le plus petit possible.
Des solutions optimales sont connues pour n < 13 et pour tout nombre triangulaire de cercle, et des conjectures sont disponibles pour n < 28[1],[2],[3].
Une conjecture de Paul Erdős et Norman Oler indique que si n est un nombre triangulaire alors les empilement optimaux de n − 1 et de n cercles ont la même longueur de côté : c'est, selon la conjecture, un empilement optimal pour n − 1 cercles peut être trouvé en supprimant un seul cercle de l'empilement hexagonal optimal de n cercles[4]. On sait maintenant que cette conjecture est vraie pour n ≤ 15[5].
Voici les solutions minimales pour la longueur du côté du triangle[1] :
| Nombre de cercles n | Longueur du côté du triangle | Figure |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | 
| |
| 5 |  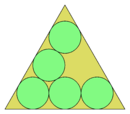
| |
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 |
Un problème étroitement lié est de couvrir le triangle équilatéral avec un nombre fixe de cercles égaux, ayant un rayon aussi petit que possible[6].
Voir aussi
modifier- Problème de Malfatti, une construction donnant la solution optimale pour trois cercles dans un triangle équilatéral.
Références
modifier- (en) Hans Melissen, « Densest packings of congruent circles in an equilateral triangle », The American Mathematical Monthly, vol. 100, no 10, , p. 916–925 (DOI 10.2307/2324212, MR 1252928).
- (en) J.B.M. Melissen et P.C. Schuur, « Packing 16, 17 or 18 circles in an equilateral triangle », Discrete Mathematics, vol. 145, nos 1-3, , p. 333–342 (DOI 10.1016/0012-365X(95)90139-C, MR 1356610).
- (en) R.L. Graham et B.D. Lubachevsky, « Dense packings of equal disks in an equilateral triangle: from 22 to 34 and beyond », Electronic Journal of Combinatorics, vol. 2, , Article 1, approx. 39 pp. (electronic) (MR 1309122, lire en ligne).
- (en) Norman Oler, « A finite packing problem », Canadian Mathematical Bulletin, vol. 4, , p. 153–155 (DOI 10.4153/CMB-1961-018-7, MR 0133065).
- Charles Payan, « Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler », Discrete Mathematics, vol. 165/166, , p. 555–565 (DOI 10.1016/S0012-365X(96)00201-4, MR 1439300).
- (en) Kari J. Nurmela, « Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles », Experimental Mathematics, vol. 9, no 2, , p. 241–250 (DOI 10.1080/10586458.2000.10504649, MR 1780209, lire en ligne).










