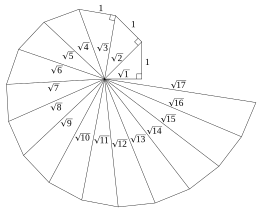
Escargot de Pythagore

L'escargot de Pythagore, « spirale de Théodore » ou encore « spirale d'Anderhub » est une figure qui permet de construire géométriquement les racines carrées des entiers consécutifs.

Escargot de Pythagore

Construction

On part d'un triangle rectangle dont les côtés de l'angle droit sont de longueur 1. Par application du théorème de Pythagore, son hypoténuse a pour longueur ${\sqrt {2}}$.

Puis, à partir de l'hypoténuse de ce triangle, on construit un nouveau triangle rectangle : l'hypoténuse du premier triangle forme un des côtés de l'angle droit du nouveau triangle, l'autre côté de l'angle droit est à nouveau de longueur 1. En appliquant de nouveau le théorème de Pythagore, l'hypoténuse de ce second triangle rectangle a pour longueur $L$ tel que $L^{2}=2+1=3$. On a donc $L={\sqrt {3}}$. On peut alors réitérer la construction, en construisant à chaque fois un nouveau triangle rectangle dont un des côtés de l'angle droit est l'hypoténuse du triangle rectangle précédent, l'autre côté de l'angle droit ayant pour longueur 1. Les longueurs des hypoténuses des triangles rectangles ainsi obtenus sont les racines carrées des entiers consécutifs.

En généralisant ce principe, un triangle avec les côtés adjacents à l'angle droit de longueur ${\sqrt {n}}$ et 1 a une hypoténuse de longueur ${\sqrt {n+1}}$.

Illustration de la génératisation de principe de construction de la spirale de Pythagore

Histoire

La première occurrence de cette construction remonte à Jakob Heinrich Anderhub, qui la surnomme « spirale de Théodore » en l'honneur de Théodore de Cyrène, qui aurait pu découvrir cette figure en son temps pour prouver l’irrationalité des racines carrées des nombres entiers non carrés jusqu'à 17. Si les travaux de Théodore sont perdus, Platon le cite dans son dialogue Théétète.

Hypoténuses

Chacune des hypoténuses des triangles $h_{n}$ donne la racine carrée de l'entier naturel correspondant, soit $h_{1}={\sqrt {2}}$.

Platon, encadré par Théodore, s'est demandé pourquoi Théodore s'arrêté à ${\sqrt {17}}$; il est communément admis que la raison est qu'il s'agit du dernier triangle qui ne vient pas se superposer à la figure

Non-superposition

En 1958, Kaleb Williams prouve qu'aucune paire d'hypoténuses ne coïncident, jusqu'à l'infini. De plus, si les côtés unitaires sont étendus en des droites, aucune ne passe par un des sommets de la figure complète.

Extension

Escargot de Théodore colorié avec 110 triangles

Théodore a arrêté la construction de la spirale à l'hypoténuse de longueur ${\sqrt {17}}$, mais en continuant l'escargot à l'infini, d'autres propriétés émergent.

Taux de croissance

Angle

En notant $\varphi _{n}$ l'angle du n^e triangle, alors : $$\tan \left(\varphi _{n}\right)={\frac {1}{\sqrt {n}}}.$$ Ainsi, la croissance de l'angle $\varphi _{n}$ du triangle suivant $n$ est: $$\varphi _{n}=\arctan \left({\frac {1}{\sqrt {n}}}\right).$$

La somme des angles des k premiers triangles est appelé angle total $\varphi (k)$ pour le k^e triangle. Elle croit proportionnellement avec la racine carrée de $k$, avec un terme correctif borné $c_{2}$: $$\varphi (k)=\sum _{n=1}^{k}\varphi _{n}=2{\sqrt {k}}+c_{2}(k)$$ où $$\lim _{k\to \infty }c_{2}(k)=-2,157782996659\ldots$$ ( A105459).

Un triangle ou section de l'escargot

Rayon

La croissance du rayon de la spirale pour un triangle n est $$\Delta r={\sqrt {n+1}}-{\sqrt {n}}.$$

Spirale d'Archimède

L'escargot de Pythagore approche la spirale d'Archimède. De même que la distance entre deux arcs de la spirale d'Archimède est égale à π, quand le nombre de tours de l'escargot de Pythagore augmente infiniment, la distance entre deux arcs consécutifs approche rapidement de π.

La table suivante montre l'évolution de cette suite de distances :

Tour No.:	Distance moyenne	Écart moyen avec π
2	3,1592037	99,44255%
3	3,1443455	99,91245%
4	3,14428	99,91453%
5	3,142395	99,97447%
$\to \infty$	$\to \pi$	$\to 100\%$

Ainsi, en cinq tours, on a déjà une bonne approximation de π.

Courbe régulière interpolante

Prolongement analytique de l'escargot de Pythagore par Philip J. Davis, incluant le prolongement dans la direction opposée (pour les entiers négatifs).

La question de l'existence d'une courbe régulière interpolant les sommets de l'escargot a été proposée et résolue par Philip J. Davis en 2001, par analogie avec la formule d'Euler pour la fonction Gamma comme interpolante de la fonction factorielle. Davis propose $$T(x)=\prod _{k=1}^{\infty }{\frac {1+\mathrm {i} /{\sqrt {k}}}{1+\mathrm {i} /{\sqrt {x+k}}}}\qquad (-1<x<\infty )$$ qui a plus longuement été étudiée par son élève Leader et Iserles. Cette fonctions est caractérisée comme l'unique solution de l'équation fonctionnelle $$f(x+1)=\left(1+{\frac {\mathrm {i} }{\sqrt {x+1}}}\right)\cdot f(x),$$ avec pour condition initiale $f(0)=1,$ et monotone en argument et module.

Un prolongement analytique de la forme continue de Davis de l'escargot de Pythagore s'étend dans la direction opposée depuis l'origine.

Voir aussi

• Spirale de Fermat
• Spirale

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Spiral of Theodorus » (voir la liste des auteurs).

Bibliographie

• (en) P. J. Davis, Spirals from Theodorus to Chaos, A K Peters/CRC Press, 2001
• (en) Detlef Gronau, « The Spiral of Theodorus », The American Mathematical Monthly, vol. 111, n^o 3,‎ mars 2004, p. 230–237 (DOI 10.2307/4145130, JSTOR 4145130)
• (en) J. Heuvers, D. S. Moak et B Boursaw, Functional Equations and Inequalities, T. M. Rassias, 2000, 111–117 p., « The functional equation of the square root spiral »
• (en) Jörg Waldvogel, « Analytic Continuation of the Theodorus Spiral », 2009