Fonction d'activation
Dans le domaine des réseaux de neurones artificiels, la fonction d'activation est une fonction mathématique appliquée à un signal en sortie d'un neurone artificiel. Le terme de "fonction d'activation" vient de l'équivalent biologique "potentiel d'activation", seuil de stimulation qui, une fois atteint entraîne une réponse du neurone. La fonction d'activation est souvent une fonction non linéaire. Un exemple de fonction d'activation est la fonction de Heaviside, qui renvoie tout le temps 1 si le signal en entrée est positif, ou 0 s'il est négatif.
Caractéristiques des fonctions d'activation
modifierLes fonctions d'activation sont utilisées selon leurs caractéristiques :
- Non-linéarité : Quand une fonction est non linéaire, un réseau neuronal à 2 couches peut être considéré comme un approximateur de fonction universel[1]. Note: La fonction identité a l'effet inverse, rendant un réseau neuronal multicouches équivalent à un réseau neuronal à une mono-couche.
- Différentiable partout : Cette propriété permet de créer des optimisations basées sur les gradients[2].
- Étendue : Quand la plage d'activation est finie, les méthodes d'apprentissage basées sur les gradients sont plus stables (impact sur un nombre de poids limités). Quand la plage est infinie, l'apprentissage est généralement plus efficace (impact sur davantage de poids).
- Monotone: Lorsque la fonction est monotone, la surface d'erreur associée avec un modèle monocouche est certifiée convexe[3].
- Douce (dérivée monotone) : Les fonctions à dérivée monotone ont été montrées comme ayant une meilleure capacité à généraliser dans certains cas. Ces fonctions permettent d'appliquer des principes comme le rasoir d'Ockham[4].
- Identité en 0 ( quand ) : Ces fonctions permettent de faire un apprentissage rapide en initialisant les poids de manière aléatoire. Si la fonction ne converge pas vers l'identité en 0, alors un soin spécial doit être apporté lors de l'initialisation des poids[5].
Liste de fonctions d'activation usuelles
modifierComparatif des principales fonctions, avec leur étendue, leur continuité, si elles sont monotones, douces et si elles convergent vers l'identité en 0.
| Nom | Graphe | Équation | Dérivée | Étendue | Ordre de continuité | Monotone | Lisse (dérivée monotone) |
Identité en 0 |
|---|---|---|---|---|---|---|---|---|
| Identité/Rampe | 
|
Oui | Oui | Oui | ||||
| Marche/Heaviside | 
|
Oui | Non | Non | ||||
| Logistique (ou marche douce, ou sigmoïde) | 
|
Oui | Non | Non | ||||
| Tangente hyperbolique | 
|
Oui | Non | Oui | ||||
| Arc tangente | 
|
Oui | Non | Oui | ||||
| Signe doux[6] | 
|
Oui | Non | Oui | ||||
| Unité de rectification linéaire (ReLU)[7] | 
|
Oui | Oui | Oui | ||||
| Unité de rectification linéaire paramétrique (PReLU)[8] | 
|
Oui | Oui | Oui | ||||
| Unité exponentielle linéaire (ELU)[9] | 
|
si |
Oui | Oui | Oui, ssi | |||
| Unité de rectification linéaire douce (SoftPlus)[10] | 
|
Oui | Oui | Non | ||||
| Identité courbée | 
|
Oui | Oui | Oui | ||||
| Exponentielle douce paramétrique (soft exponential)[11] | 
|
Oui | Oui | Oui, ssi | ||||
| Sinusoïde | 
|
Non | Non | Oui | ||||
| Sinus cardinal | 
|
Non | Non | Non | ||||
| Fonction gaussienne | 
|
Non | Non | Non | ||||
| Swish ou SiLU (Sigmoid Linear Unit)[12] | 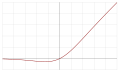
|
= | (si ) | Non | Non | Oui |
Structures alternatives
modifierUne classe spéciale de fonction d'activation est regroupée dans les fonctions à base radiale (RBFs). Elles sont souvent utilisées dans les réseaux neuronaux RBF, très efficaces en tant qu'approximations de fonctions universelles. Si ces fonctions peuvent être très variées, on retrouve généralement une des trois formes suivantes (en fonction d'un vecteur v :
- Fonction gaussienne :
- Fonction multiquadratique :
- Fonction multiquadratique inverse:
où ci est le vecteur représentant le centre de la fonction, a est un paramètre permettant de régler l'étalement de la fonction.
Les machines à support vectoriel (SVMs) peuvent utiliser une classe de fonctions d'activation qui inclut à la fois les sigmoïdes et les RBF. Dans ce cas, l'entrée est transformée pour refléter un decision boundary hyperplane, basé sur peu d'entrées (appelées vecteurs support x. La fonction d'activation pour les couches cachées de ces machines est souvent appelée "noyau du produit intérieur" : . Les vecteurs supports sont représentés comme les centres de RBF dont le noyau serait égal aux fonctions d'activation, mais ils prennent une unique forme de perceptron :
- ,
Où et doivent satisfaire certains critères de convergence. Ces machines peuvent aussi accepter des fonctions d'activation polynomiale d'un ordre arbitraire[13]:
- .
Voir aussi
modifierRéférences
modifier- ↑ (en) George Cybenko, « Approximation by superpositions of a sigmoidal function », Mathematics of control, signals and systems, vol. 2, no 4, , p. 303-314.
- ↑ (en) Jan Snyman, Practical mathematical optimization: an introduction to basic optimization theory and classical and new gradient-based algorithms, vol. 97, Springer Science & Business Media, .
- ↑ (en) Huaiqin Wu, « Global stability analysis of a general class of discontinuous neural networks with linear growth activation functions », Information Sciences, vol. 179, no 19, , p. 3432-3441.
- ↑ (en) Michael S. Gashler et Stephen C. Ashmore, « Training Deep Fourier Neural Networks to Fit Time-Series Data », Intelligent Computing in Bioinformatics, Springer International Publishing, , p. 48-55 (« 1405.2262 », texte en accès libre, sur arXiv.)
- ↑ (en) David Sussillo et L. F. Abbott, « Random walks: Training very deep nonlinear feed-forward networks with smart initialization », CoRR, vol. 286, (« 1412.6558 », texte en accès libre, sur arXiv.).
- ↑ (en) Xavier Glorot et Yoshua Bengio, « Understanding the difficulty of training deep feedforward neural networks », Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS’10), Society for Artificial Intelligence and Statistics, (lire en ligne)
- ↑ (en) Vinod Nair et Geoffrey Hinton, « Rectified linear units improve restricted boltzmann machines », Proceedings of the 27th International Conference on Machine Learning (ICML-10),
- ↑ (en) Kaiming He, Xiangyu Zhang, Shaoqing Ren et Jian Sun, « Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification », Computer Vision and Pattern Recognition, « 1502.01852 », texte en accès libre, sur arXiv.
- ↑ (en) Djork-Arné Clevert, Thomas Unterthiner et Sepp Hochreiter, « Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs) », Machine Learning, « 1511.07289v3 », texte en accès libre, sur arXiv.
- ↑ (en) Xavier Glorot, Antoine Bordes et Yoshua Bengio, « Deep sparse rectifier neural networks », International Conference on Artificial Intelligence and Statistics,
- ↑ (en) Luke B. Godfrey et Michael S. Gashler, « A Continuum among Logarithmic, Linear, and Exponential Functions, and Its Potential to Improve Generalization in Neural Networks », Proceedings of the 7th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management: KDIR, Lisbonne, Portugal, , p. 481-486, « 1602.01321 », texte en accès libre, sur arXiv.
- ↑ (en) Prajit Ramachandran, Barret Zoph et Quoc V. Le, « Searching for Activation Functions », Proceedings of ICLR 2018, , « 1710.05941 », texte en accès libre, sur arXiv.
- ↑ (en) Simon Haykin, Neural Networks : A Comprehensive Foundation, Prentice Hall, , 2e éd., 842 p. (ISBN 0-13-273350-1)












![{\displaystyle [0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc3bf59a5da5d8181083b228c8933efbda133483)


![{\displaystyle [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf)


![{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)

























![{\displaystyle [\sim -0,217234...;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fe3d3802e91b6e1d8f966cdcc48f40fab3d4bba)


![{\displaystyle ]0;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce0afd2865e794abecc52498533cd63249990e8)



![{\displaystyle ]-{\rm {e}};\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d43977231b871febb1ad7b6de3f3713b5985478f)








