Pentachore rectifié
En géométrie à quatre dimensions, le Pentachore rectifié, ou 5-cellules rectifié, est un polytope uniforme à 4 dimensions (ou polychore uniforme) composé de 5 cellules tétraédriques régulières et de 5 cellules octaédriques régulières. Chaque arête est adjacente à un tétraèdre et deux octaèdres. Chaque sommet est entouré de deux tétraèdres et trois octaèdres. Au total, le pentachore rectifié possède 30 faces triangulaires, 30 arêtes et 10 sommets.
| Pentachore rectifié (5-cellules rectifié) | |
 Diagramme de Schlegel (5 cellules tétraédriques) | |
| Type | Polychore uniforme semi-régulier |
|---|---|
| Configuration de sommet | 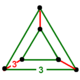 Prisme triangulaire |
| Cellules | 10 : 5 tétraèdres + 5 octaèdres |
| Faces | 30 Triangles équilatéraux |
| Arêtes | 30 |
| Sommets | 10 |
| Symbole de Schläfli | t 1 {3,3,3} ou r{3,3,3} {3 2,1 } = |
| Polygone de Pétrie | Pentagone |
| Groupe(s) de Coxeter | A 4, [3,3,3], ordre 120 |
| Diagramme de Coxeter-Dynkin | |
| Propriétés | Convexe, isogonal, isotoxal |
| modifier |
|
La figure de sommet du pentachore rectifié est un prisme triangulaire uniforme, formé de trois carrés (correspondant aux trois octaèdres présents au sommet) et de deux triangles équilatéraux (correspondant aux deux tétraèdres, à ce même sommet).
Bien qu'ayant le même nombre de sommets que de cellules (10), et le même nombre d'arêtes que de faces (30), le pentachore rectifié n'est pas autodual car la figure de sommet n'est pas un dual des cellules du polychore. Le dual du pentachore rectifié est le pentachore joint[1], un polychore de Catalan constitué de 10 cellules bipyramidales triangulaires à faces triangulaires isocèles, 30 triangles isocèles, 30 arêtes (10 longues, 20 courtes) et 10 sommets.
Noms alternatifs
modifier- Tétroctaédrique (Thorold Gosset)
- Dispentachoron
- 5-cellules rectifié (Norman W. Johnson)
- 4-simplex rectifié
- 4-simplex entièrement tronqué
- Pentachoron rectifié (Jonathan Bowers)
- rap (Notation de Jonathan Bowers)
- Ambopentachoron (Neil Sloane et John Horton Conway)
- (5,2)-hypersimplex : l'enveloppe convexe des vecteurs à cinq dimensions avec exactement deux "1" et trois "0", obtenus par permutation de (0,0,0,1,1).
Structure
modifierLe pentachore rectifié peut être obtenu par rectification du pentachore, c'est-à-dire en tronquant chaque sommet du pentachore jusqu'à la moitié des arêtes. Les cinq tétraèdres réguliers deviennent des tétraèdres rectifiés, donc des octaèdres réguliers, et cinq nouveaux tétraèdres réguliers sont produits.
Partant du pentachore, dont le Symbole de Schläfli est noté {3,3,3}, le Symbole de Schläfli étendu du pentachore rectifié est noté t1{3,3,3} ou r{3,3,3}. A noter que la rectification du pentachore rectifié (un pentachore birectifié, de Symbole de Schläfli t2{3,3,3} ou 2r{3,3,3}) est égale à la rectification du dual du pentachore (dual noté t3{3,3,3} ou 3r{3,3,3}), c'est-à-dire à la rectification du pentachore - le pentachore étant autodual - et est donc aussi un pentachore rectifié[2].
Le pentachore rectifié est ainsi l'un des neuf polychores uniformes construits à partir du pentachore :
| Troncatures du pentachore | Pentachore | Pentachore tronqué | Pentachore rectifié | Pentachore biseauté | Pentachore bitronqué | Pentachore biseauté-tronqué | Pentachore augmenté | Pentachore augmenté-tronqué | Pentachore omnitronqué |
|---|---|---|---|---|---|---|---|---|---|
| Symbole de Schläfli | {3,3,3} 3r{3,3,3} |
t{3,3,3} 3t{3,3,3} |
r{3,3,3} 2r{3,3,3} |
rr{3,3,3} r2r{3,3,3} |
2t{3,3,3} | tr{3,3,3} t2r{3,3,3} |
t0,3{3,3,3} | t0,1,3{3,3,3} t0,2,3{3,3,3} |
t0,1,2,3{3,3,3} |
| Diagramme de Coxeter | |||||||||
| Diagramme de Schlegel | 
|

|

|

|

|

|

|

|

|
| Projection orthogonale par le plan de Coxeter A4 | 
|
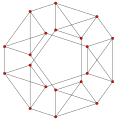
|

|

|

|

|
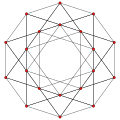
|

|

|
| par le plan de Coxeter A3 | 
|

|

|

|

|

|

|

|

|
| par le plan de Coxeter A2 | 
|

|

|

|

|

|

|
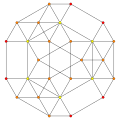
|

|
Avec le pentachore et l'icositétrachore, le pentachore rectifié et son dual étaient les premiers 4-polytopes 2-simpliciaux 2-simples connus, c'est-à-dire que toutes leurs faces et toutes les faces de leur dual sont des triangles. En 1997, Tom Braden a trouvé une autre paire duale, en collant deux pentachores rectifiés ensemble ; depuis lors, une infinité de polytopes 2-simpliciaux 2-simples ont été construits[3],[4].
Polytope semi-régulier
modifierC'est l'un des trois polychores semi-réguliers, constitués de deux ou plusieurs cellules formant des solides platoniciens (polyèdres réguliers convexes). Découverts par Thorold Gosset dans son article de 1900, ce dernier l'a appelé tétractaédrique car ce polychore est constitué de cellules tétraédriques et octaédriques.
E. L. Elte l'a identifié en 1912 comme un polytope semi-régulier, le désignant par le symbole tC 5[5].
Construction de Wythoff
modifierLa matrice de configuration suivante montre les comptages d'incidence entre les éléments. Les nombres du vecteur f en diagonale sont dérivés par la construction de Wythoff, en divisant l'ordre du groupe complet (A4, d'ordre 5!, correspondant au pentachore rectifié) par l'ordre du sous-groupe obtenu en supprimant un miroir à la fois.
| A4 | k-face | fk | f0 | f1 | f2 | f3 | k-figure | Notes | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A2A1 | ( ) | f0 | 10 | 6 | 3 | 6 | 3 | 2 | {3}x{ } | A4/A2A1 = 5!/3!/2 = 10 | |
| A1A1 | { } | f1 | 2 | 30 | 1 | 2 | 2 | 1 | { }v( ) | A4/A1A1 = 5!/2/2 = 30 | |
| A2A1 | {3} | f2 | 3 | 3 | 10 | * | 2 | 0 | { } | A4/A2A1 = 5!/3!/2 = 10 | |
| A2 | 3 | 3 | * | 20 | 1 | 1 | A4/A2 = 5!/3! = 20 | ||||
| A3 | r{3,3} | f3 | 6 | 12 | 4 | 4 | 5 | * | ( ) | A4/A3 = 5!/4! = 5 | |
| A3 | {3,3} | 4 | 6 | 0 | 4 | * | 5 | ||||
Images
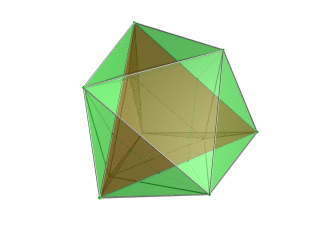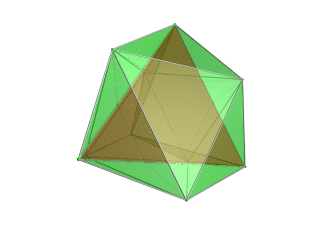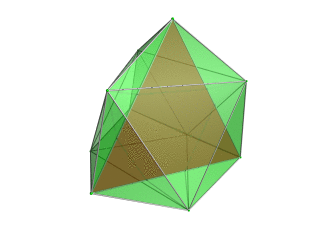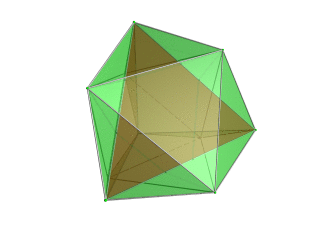
modifier projection stéréographique (centré sur l'octaèdre) |

|
|
Projection en perspective centrée sur le tétraèdre dans l'espace 3D, avec le tétraèdre le plus proche du point de vue 4D rendu en rouge et les 4 octaèdres environnants en vert. Les cellules situées de l'autre côté du polytope ont été éliminées pour plus de clarté (bien qu'elles puissent être discernées à partir des contours des bords). La rotation concerne uniquement l'image de projection 3D, afin de montrer sa structure, pas une rotation dans l'espace 4D. |
Coordonnées
modifierLes coordonnées cartésiennes des sommets du pentachore rectifié centré sur l'origine et ayant une longueur d'arête égale à 2 sont :
| Coordonnées | |
|---|---|
|
|
|
Les sommets du pentachore rectifié peuvent être positionnés sur un hyperplan de l'espace de dimension 5 par des vecteurs obtenus par les permutations de (0,0,0,1,1) et de (0,0,1,1,1).
Polychores apparentés
modifierLe pentachore rectifié est la figure de sommet du 5-demicube ; c'est aussi la figure d'arête du polytope uniforme de dimension 6 noté 221 (en).
Composé du pentachore rectifié et de son dual
modifierL'enveloppe convexe du pentachore rectifié et de son dual de même grand rayon est un polychore non uniforme composé de 30 cellules : 10 tétraèdres et 20 octaèdres (les octaèdres sont des antiprismes triangulaires), et 20 sommets. Sa figure de sommet est un bifrustum triangulaire (tronc de bipyramide triangulaire).
Polytopes de pentachore
modifierLe pentachore rectifié est l'un des 9 polytopes uniformes à 4 cellules construits à partir du groupe de Coxeter [3,3,3].
Polytopes semi-réguliers
modifierLe pentachore rectifié est le deuxième élément d'une série dimensionnelle de polytopes semi-réguliers. Chaque polytope uniforme est construit comme la figure de sommet du polytope précédent. Thorold Gosset a identifié cette série en 1900 comme contenant toutes les facettes de polytopes réguliers, contenant tous les simplexes et orthoplexes (tétraèdres et octaèdres dans le cas du pentachore rectifié). Le symbole de Coxeter du pentachore rectifié est 021.
Notes et références
modifierNotes
modifier- ↑ (en) « The Joined Pentachoron », sur 4D Euclidean space, (consulté le ).
- ↑ Alain Gottcheiner, Constructions et taxonomies de polytopes combinatoires, Université libre de Bruxelles, Faculté des sciences appliquées (thèse de doctorat), 2001-2002 (lire en ligne), p. 100-104
- ↑ David Eppstein, Greg Kuperberg et Günter M. Ziegler, « Discrete Geometry: In honor of W. Kuperberg's 60th birthday », (arXiv math.CO/0204007), p. 239–265.
- ↑ Andreas Paffenholz et Günter M. Ziegler, « The Et-construction for lattices, spheres and polytopes », Discrete & Computational Geometry, (DOI 10.1007/s00454-004-1140-4, MR 2096750, arXiv math.MG/0304492, S2CID 7603863), p. 601–621.
- ↑ E. L. Elte, « The semiregular polytopes of the hyperspaces », Dissert. Univ. Groningen, sur ResearchGate
Références
modifier- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Rectified 5-cell » (voir la liste des auteurs).
- (en) John Conway, Heidi Burgiel et Chaim Goodman-Strauss (en), The Symmetries of Things, CRC Press, (ISBN 978-1-56881-220-5, lire en ligne), chap. 26.
- John Conway et MJT Guy, Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity, Copenhague, pages 38 et 39, 1965.
- H. S. M. Coxeter :
- (en) Regular Polytopes, New York, Dover Publications, , 3e éd. (ISBN 0-486-61480-8).
- Kaléidoscopes : Selected Writings of H.S.M. Coxeter, édité par F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, (ISBN 978-0-471-01003-6) [lire en ligne].
- Article 22 : Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10].
- Article 23: Regular and Semi Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591].
- Article 24: Regular and Semi Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45].
- T. Gosset : On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900.
- Norman Johnson :
- Uniform Polytopes, manuscrit, 1991.
- The Theory of Uniform Polytopes and Honeycombs, Ph.D., 1966.
Liens externes
modifier- (de) « Archimedisches Polychor Nr. 3 (Rectified 5-cell) »
- (en) « 1. Convex uniform polychora based on the pentachoron (5-cell) »
- (en) « 4D polytopes (Polychora) »







