Horizon optique

L'horizon optique est la ligne circulaire où la terre et le ciel semblent se rejoindre et qui limite le champ visuel d'une personne en un lieu ne présentant pas d'obstacle à la vue. C'est aussi la limite divisant la sphère terrestre en deux parties, l'une visible de l'observateur, l'autre invisible. La Terre étant presque sphérique, elle a une courbure — dite « courbure terrestre », aussi appelée « abaissement » ou « dépression de l'horizon » — qui provoque un phénomène observable à l'horizon optique : au delà de cette limite, la partie haute de certains objets peut encore être visible, alors que leur partie basse est cachée à l'observateur.

Éoliennes à grande distance partiellement cachées derrière la ligne d'horizon.

La courbure terrestre limite la possibilité d'observer des objets à une distance lointaine.

Il existe plusieurs méthodes permettant de calculer la distance de l'horizon optique en fonction de l'altitude du point d'observation, ainsi que la hauteur minimale des points partiellement visibles situés au-delà de cette distance.

Première approche : distance de l'horizon en ligne droite

La notion de puissance d'un point par rapport à un cercle, décrite par Euclide dans le livre III des Eléments, proposition 36, permet de démontrer que, quel que soit le segment sécant mené d'un point P extérieur à un cercle de centre O, de rayon R et le coupant en des points A et B, on a :

$PA\times PB=constante=PO^{2}-R^{2}$.

Le point limite de vision d'un observateur situé en P est le point T situé sur la droite qui passe par le point P et qui est tangente en T à la Terre, d étant la distance entre le point d'observation P et l'horizon visuel en T, et h étant l'altitude du point d'observation, on a :

Puissance d'un point par rapport à un cercle.

$d^{2}=PO^{2}-R^{2}=(h+R)^{2}-R^{2}$.

Donc :

$d={\sqrt {h\times (2\times R+h)}}$.

En considérant que la Terre est quasiment sphérique et que le rayon de la Terre est de 6 378 km, cette formule devient, avec h et d mesurés en km :

$d={\sqrt {h\times (12\,756+h)}}$.

Le tableau ci-dessous indique plusieurs exemples de distance de l'horizon optique d, en fonction de l'altitude h du point d'observation.

Distance d de l'horizon optique en fonction de l'altitude h du point d'observation

h (m)	d (km)
1,7	4,7
3,0	6,2
10	11,3
30	19,6
50	25,3
100	35,7
500	79,9
1 000	112,9
2 000	159,7
4 000	225,9
8 000	319,5

Ainsi, depuis le sommet du mont Blanc (h = 4 806 m), la distance de l'horizon optique approche les 250 km, alors que, depuis le sommet de la tour Eiffel (h = 320 m environ), cette distance est proche de 64 km. Quant à la distance de l'horizon depuis l'Everest, plus haute montagne sur Terre culminant à 8 849 m, elle dépasse les 330 km.

Deuxième approche : distance de l'horizon mesurée à la surface de la Terre

Détermination de la hauteur h du bord du cercle B à la droite tangente au cercle au point A.

Cette technique est proche de celle utilisée par Ératosthène pour déterminer le rayon de la Terre.

En considérant que la Terre est une sphère de rayon R, on peut calculer comment varie la courbure au fur et à mesure que l'on s'éloigne d'un point A, c'est-à-dire à quelle hauteur h se trouverait un rayon de lumière lancé à l'horizontale de A, vu depuis un point B distant sur Terre de d = AB (d = distance courbe sur la sphère).

d est la longueur d'un arc de cercle, correspondant à un angle au centre qui, exprimé en radians (rad), vaut : α = d/R.

Dans ce cas, on calcule :

$d=R\times \arccos \left({\frac {R}{R+h}}\right)$.

Cette distance d est la distance mesurée à la surface de la Terre entre le « pied » du point d'observation (B) et l'horizon (A).

On a également :

$h={\frac {R}{\cos \alpha }}-R=R\times \left({\frac {1}{\cos \alpha }}-1\right)=R\times \left({\frac {1}{\cos \left({\frac {d}{R}}\right)}}-1\right)$.

Cette hauteur h est la hauteur maximale en B d'un objet qui sera invisible depuis A, et c'est aussi la hauteur minimale en B d'un objet dont la partie haute est visible de A.

Le graphique ci-dessous donne les valeurs de h en fonction de d pour un rayon terrestre de 6 378 km.

Une variante de cette deuxième approche, utilisant le même cercle ci-dessus, consiste à appliquer le théorème de Pythagore.

On a alors (R+h)² = R² + d²

Puis d² = (R+h)² - R²

Et enfin $d={\sqrt {(R+h)^{2}-R^{2}}}$

Troisième approche : points mutuellement visibles

Détermination de la hauteur h₂ du bord du cercle B à la droite tangente au cercle partant d'une hauteur h₁ en A.

On calcule ici quelle sera la hauteur h₂ cachée en B à un observateur placé en A à l'altitude h₁ à une distance (sur la sphère) de d = AB sur la sphère de rayon R.

On calcule la distance :

${\overset {\frown }{BC}}=d-{\overset {\frown }{CA}}=d-R\times \arccos \left({\frac {R}{R+h_{1}}}\right)$

et on obtient :

$h_{2}=R\times \left({\frac {1}{\cos({\frac {\overset {\frown }{BC}}{R}})}}-1\right)=R\times \left({\frac {1}{\cos({\frac {d}{R}}-\arccos({\frac {R}{R+h_{1}}}))}}-1\right)$

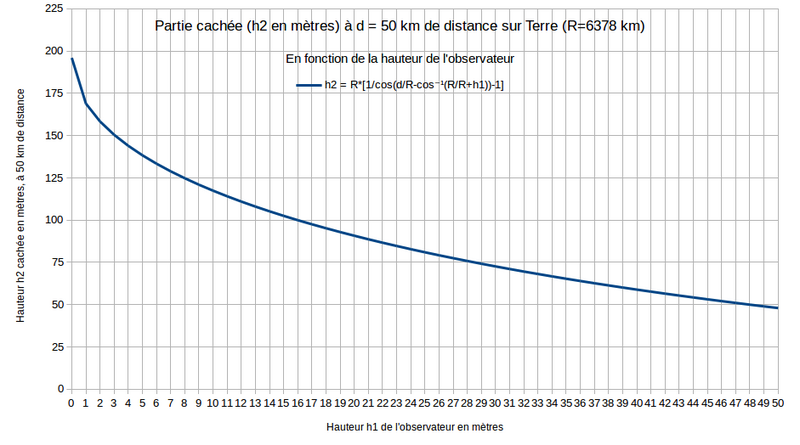
h₂ est la hauteur maximale en B d'un objet qui sera invisible à un observateur situé en A à l'altitude h₁, et c'est aussi la hauteur minimale en B d'un objet dont la partie haute est visible de cet observateur.

Avec R = 6 378 km et d = 50 km entre les deux points d'observation, le graphique ci-dessous illustre comment la hauteur cachée h₂ décroît à mesure que h₁ augmente :

Hauteur cachée h₂ en mètres selon la hauteur en mètres h₁ d'un observateur placé à une distance d = 50 km sur une sphère de rayon R = 6 378 km.

Conséquences et applications pratiques

Altitude du point d'observation

Plus l'altitude du point d'observation -ou plus généralement d'émission/réception dans le cas de toutes les ondes électromagnétiques - est élevée, plus l'horizon optique est lointain. Ainsi, chaque fois qu'on quadruple la hauteur d'un point d'observation, on double la distance de vision.

C'est pour cette raison que les systèmes conçus pour observer ou être visibles à grande distance sont placés en hauteur :

• les feux des phares sont placés dans des positions aussi élevées que possible malgré l'augmentation de coût que cela implique dans leur construction ;
• les hunes d'observation des navires sont placées en hauteur dans la mâture ;
• les emplacements équipés du télégraphe de Chappe (XVIII^e siècle) sont sur des points hauts ;
• les miradors et tours d'observation sont placés et construits de façon à dominer leur environnement immédiat ;
• les émetteurs d'ondes servant à la télévision analogique ou numérique, à la radio ou aux communications mobiles sont placés sur des points hauts pour augmenter leur zone de couverture.

• 
  Phare du Portzic, Bretagne, France.
• 
  Frégate Hermione à Rochefort. La hune est la plate-forme visible au deux tiers du grand mât.
• 
  Tour Chappe à Marly-le-Roi. Elle faisait partie de la liaison télégraphique Paris-Brest.
• 
  Tour du Guet, Calais, France.
• 
  Tour hertzienne à Lisses, Essonne, France.

Distance de vision inférieure à la distance théorique

La zone rouge est cachée à l'observateur par l'obstacle.

Les valeurs réelles de distance de vision peuvent être sensiblement inférieures à celles indiquées par la théorie. Plusieurs facteurs peuvent en effet diminuer cette distance, notamment :

• obstacle : un obstacle situé entre le point d'observation et l'horizon théorique (par exemple : arbre, immeuble, montagne) empêche de voir certains objets, pourtant théoriquement visibles, situés au delà de cet obstacle ;
• brouillard, faible luminosité : si l'atmosphère est obscurcie par du brouillard, ou si la luminosité est très faible (exemple : nuit sans Lune), la distance de vision optique d'un observateur humain sera fortement diminuée ;
• atténuation par l'atmosphère : la traversée de l'atmosphère affaiblit la puissance des ondes électromagnétiques. Cet affaiblissement dépend de paramètres caractérisant l'atmosphère, de la distance parcourue par ces ondes, ainsi que de leur fréquence. Il peut diminuer fortement la zone de couverture théorique d'un émetteur radioélectrique.

Limites liées à l'acuité de la vision humaine

L'œil humain a un pouvoir de résolution limité : pour pouvoir distinguer deux points, l'œil doit les voir sous un angle apparent de plus d'une minute d'arc. Ceci implique qu'un observateur humain ne verra un objet lointain, même situé avant l'horizon optique, que s'il a une taille suffisante. Cette taille vaut, avec h et d en mètres, et α en radians :

$h=2\times (d\times \sin(\alpha /2))$.

Pour des angles apparents faibles, on a, avec $\alpha$ en radians :

$h\simeq d\times \alpha$.

Et pour $\alpha$ = 1' d'arc, cette formule devient :

$h\simeq d\times (2\times \Pi )/(60*360)$.

Avec h en m et d en km, cette formule devient :

$h\simeq 0,29\times d$.

Ainsi un observateur situé à 1,7 m d'altitude ne verra à l'horizon (distant de 4,7 km) que les objets ayant une taille d'au moins 1,36 m. Ce même observateur d'une altitude de 30 m aura un horizon à environ 20 km, et ne verra d'objets à cette distance que s'ils ont un taille d'au moins 5,7 m.

L'utilisation de dispositifs optiques tels que jumelles, lunette d'observation ou longue-vue ne permet pas à cet observateur de voir plus loin : sa ligne d'horizon optique dépend en effet uniquement de son altitude. En revanche, grâce au pouvoir grossissant de ces équipements, il pourra voir des objets bien plus petits que ceux visibles à l'œil nu. Ainsi, avec un facteur de grossissement de 10, l'observateur situé à une altitude de 1,7 m verra à l'horizon des objets de 0,14 m, et celui situé à 30 m d'altitude des objets de 0,57 m.

• 
  L'œil ne distingue deux points distincts que s'il les voit avec un angle d'au moins 1' d'arc.
• 
  Jumelles de grossissement 8.
• 
  Longue-vue télescopique de marine.
• 
  Lunette fixe d'observation sur l'Arc de Triomphe à Paris.

Réfraction atmosphérique et augmentation de la distance de vision

Les calculs théoriques de distance de l'horizon optique prennent pour hypothèse que les ondes se propagent en ligne droite. En réalité, les ondes électromagnétiques traversant de façon oblique l'atmosphère terrestre sont déviées durant cette traversée. Ce phénomène est dû à la réfraction atmosphérique. L'importance de cette déviation dépend notamment de l'angle de cette traversée par rapport à la verticale, des caractéristiques de l'atmosphère (composition gazeuse, pollution, gradients de température, pression ou encore taux d'humidité) et de la fréquence de ces ondes. Lorsqu'elles sont l'objet de ce phénomène, les ondes, au lieu de se propager en ligne droite, le font en selon des trajectoires courbes. En conséquence, la réfraction, lorsqu'elle se produit, permet, d'un point d'observation donné, de voir plus loin que ne le prédit le calcul théorique, ainsi que l'illustrent les exemples suivants :

• de Marseille on ne peut normalement pas voir le sommet du Canigou distant de 250 km : pour le voir, il faudrait être à une altitude d'environ 300 m, alors que le point le plus élevé de Marseille n'est qu'à 242 m. Cependant, grâce à la réfraction, les Marseillais peuvent parfois voir cette montagne des Pyrénées en ombre chinoise sur un soleil couchant au-dessus de la Méditerranée ;
• les habitants de la Côte d'Azur et les Monégasques peuvent certains jours, même depuis le niveau de la mer, apercevoir la côte montagneuse nord de la Corse pourtant distante de 170 km.

S (en jaune) est la position réelle du Soleil. S' (en rouge) est la position apparente vue par un observateur dont la ligne d'horizon est la droite bleue.

La réfraction atmosphérique est également très importante en astronomie : ainsi, le soir, alors que le calcul théorique indique que le Soleil ne devrait plus être visible, on peut encore le voir. En effet la réfraction relève la trajectoire des rayons lumineux provenant du Soleil de 36 minutes d'arc ce qui rend le Soleil visible encore plusieurs minutes.

Réfutation du mythe de la Terre plate

La théorie de la Terre plate affirme que la Terre n'est pas ronde, mais plate. Il y a de nombreuses preuves scientifiques démontrant que cette théorie est un mythe, et que la Terre est bien ronde.

La courbure de la Terre explique la disparition progressive du bateau à l'horizon.

L'une de ces preuves est fournie par la vision qu'un observateur a des objets qui s'éloignent vers l'horizon. Ainsi une personne postée au bord de la mer qui observe un bateau à voile s'éloignant vers l'horizon le voit progressivement disparaitre : la coque passe la première sous l'horizon, puis le bas des mâts et des voiles, et enfin la totalité du navire disparait. C'est une conséquence de la courbure terrestre, bien connue des marins et très facile à observer.

Au contraire, si la Terre était plate, le navire se réduirait en taille apparente en s'éloignant, mais, à tout moment, l'observateur verrait la totalité du navire, de la coque au sommet des mâts.

Courbure et distance de l'horizon sur d'autres objets célestes

Tous les objets célestes qui ont une forme sphérique, ou sphéroïde, ont une courbure. C'est le cas de la Terre mais aussi, par exemple, de la Lune et du Soleil. On peut donc calculer avec les mêmes méthodes la distance de l'horizon optique sur de tels astres.

Ainsi, pour un observateur de 1,7 m, l'horizon est à 4,7 km sur Terre, mais seulement à 2,4 km sur la Lune, qui a un rayon quatre fois plus petit que celui de la Terre. Sur le Soleil, ce même observateur verrait l'horizon à près de 50 km, car le Soleil a un rayon de l'ordre de 700 000 km.

Voir aussi

• Horizon (physique)
• Zone de couverture des ondes radio
• Figure de la Terre
• Géodésie