Arithmétique modulaire

En mathématiques, et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes permettant la résolution de problèmes sur les nombres entiers. Ces méthodes dérivent de l’étude du reste obtenu par une division euclidienne.

Couverture de l’édition originale des Recherches arithmétiques de Gauss, livre fondateur de l’arithmétique modulaire.

L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose. Quand on fait par exemple une preuve par neuf à l'école primaire, on effectue un peu d'arithmétique modulaire sans le savoir : le diviseur est alors le nombre 9.

Si ses origines remontent à l’Antiquité, les historiens associent généralement sa naissance à l’année 1801, date de la publication du livre Disquisitiones arithmeticae de Carl Friedrich Gauss. Sa nouvelle approche permet d’élucider de célèbres conjectures et simplifie les démonstrations d’importants résultats par une plus grande abstraction. Si le domaine naturel de ces méthodes est la théorie des nombres, les conséquences des idées de Gauss se retrouvent dans d’autres champs des mathématiques, comme l’algèbre ou la géométrie.

Le XX^e siècle modifie le statut de l’arithmétique modulaire. L'arithmétique de base des ordinateurs, celle qui travaille sur des mots mémoire de taille fixe, est nécessairement une arithmétique modulaire. Le développement de nombreuses applications industrielles impose la mise au point d’algorithmes pour l'arithmétique modulaire. Ils résolvent essentiellement des questions soulevées par le développement de l'informatique.

L’article « Congruence sur les entiers » propose une introduction plus mathématique ; « Anneau ℤ/nℤ » traite le même sujet de manière moins didactique et plus exhaustive.

Usages

En mathématiques pures, ce terme est très peu utilisé. La théorie algébrique des nombres désignant un domaine beaucoup plus large contenant par exemple les notions d'entiers algébriques et de théorie de Galois.

En mathématiques appliquées, cette expression est d'un usage fréquent pour décrire les bases mathématiques de différents domaines de la théorie de l'information : cryptologie, théorie des codes et informatique. De nombreux outils et algorithmes entrent dans ce champ d'étude. Parmi les tests de primalité les plus utilisés, l'utilisation des caractères d'un groupe par exemple pour la transformée de Fourier discrète.

Selon les différents auteurs et le domaine d'application, ces extensions sont considérées, soit comme une partie intégrante de l'arithmétique modulaire^{[réf. nécessaire]}, soit comme des applications, voire ne sont pas citées du tout. Sous sa forme simple, elle prend parfois le nom d'arithmétique de l'horloge.

Les systèmes modulaires de représentation (en) (Residue number system, RNS en abrégé), des représentations des entiers fondée sur le théorème des restes chinois, sont utilisés pour accélérer les opérations de l'arithmétique modulaire.

Histoire

Origines

Couverture de l'édition de 1621 de Arithmetica de Diophante, traduite en latin par Claude-Gaspard Bachet de Méziriac.

Au III^e siècle av. J.-C., Euclide formalise, dans son livre les Éléments, les fondements de l'arithmétique. On y trouve notamment le lemme couramment nommé lemme d'Euclide, une version datée du théorème fondamental de l'arithmétique et une étude sur les nombres parfaits dans la proposition 36 de son livre IX. Diophante d'Alexandrie (env. 250) écrit son Arithmetica qui contient 130 équations. Il traite essentiellement de problèmes ayant une unique solution numérique et à valeur fractionnaire ou entière. On y trouve que les nombres sommes de deux carrés parfaits ne sont jamais de la forme 4n + 3. Les équations, à coefficients entiers et dont les solutions recherchées sont entières, prennent aujourd'hui le nom d'équations diophantiennes.

La Chine développe parallèlement une arithmétique modulaire. Sun Zi écrit vers l'an 300 un traité de mathématiques dont le problème 26 du chapitre 3 est le suivant : « Soient des objets dont on ignore le nombre. En les comptant 3 par 3 il en reste 2, en les comptant 5 par 5, il en reste 3 et en les comptant 7 par 7, il en reste 2. Combien y a-t-il d'objets ? ».

Qin Jiushao (1202 - 1261) développe le théorème des restes chinois. Son traité est remarquablement avancé ; il traite d'un système de congruences linéaires dans le cas où les moduli ne sont pas premiers entre eux deux à deux. Ses travaux sur les systèmes de congruences dépassent en sophistication ceux de Leonhard Euler. On peut citer George Sarton pour qui : « Qin Jiushao était l'un des plus grands mathématiciens de sa race, de son temps et à vrai dire de tous les temps. »

Le XIV^e siècle voit un déclin progressif puis un oubli de ces résultats, le savoir de Qin Jiushao ne dépasse pas les frontières chinoises avant le XX^e siècle. Il est redécouvert par les travaux de l'historien des sciences Joseph Needham. En revanche, de nombreuses similarités entre les notations arabes et chinoises laissent penser à des contacts durant les périodes précédentes.

L'Inde possède aussi une tradition forte en arithmétique. Aryabhata (476 - 550) recherche de manière systématique les solutions entières de l'équation linéaire à deux inconnues à coefficients entiers. Il utilise pour cela un algorithme appelé « Kuttaka » publié dans son livre appelé Âryabhatîya. Les équations diophantiennes de degré deux sont étudiées par Brahmagupta (598 - 668). Au XII^e siècle, Bhāskara II met au point la méthode chakravala.

La civilisation islamique joue un double rôle en arithmétique : elle véhicule le savoir acquis par les Grecs, Indiens, Chinois et Européens, et elle apporte des connaissances nouvelles notamment sur l'étude des propriétés de certains ensembles d'entiers, comme les nombres premiers, parfaits, amicaux ou figurés. Dans ce contexte, Qusta ibn Lûqâ réalise une traduction partielle de l'Arithmetica de Diophante d'Alexandrie à la fin du IX^e siècle et Al-Hajjaj traduit à la même époque les Éléments d'Euclide ; son collègue al-Khuwārizmī (env. 783 - env. 850) écrit un livre sur la numération indienne. Si le livre est perdu, il reste connu par une traduction latine Algoritmi de numero Indorum. Thābit (836 - 901) étudie les nombres amicaux et les nombres parfaits. Alhazen (965 - 1039) continue ses travaux sur les nombres parfaits et découvre le théorème de Wilson.

Apparition en Europe

Pierre de Fermat développe largement l'arithmétique. Les propriétés de la division euclidienne, fondement de l'arithmétique modulaire, sont largement utilisées par ce mathématicien.

En 1621, Claude-Gaspard Bachet de Méziriac traduit le livre de Diophante en latin. Les questions soulevées intéressent les mathématiciens de l'époque. Pierre de Fermat propose un grand nombre d'énoncés, les trois plus célèbres étant probablement son grand théorème, son théorème des deux carrés et son petit théorème. La communauté scientifique se lance des défis sur ce sujet, ainsi Fermat demande : « un nombre carré qui, ajouté à la somme de ses parties aliquotes (i.e. ses diviseurs), fasse un cube. » Il conclut par : « j'attends la solution de ces questions ; si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise ». Marin Mersenne recherche des nombres premiers particuliers. Fermat lui écrit : « Si je puis une fois tenir la raison fondamentale que 3, 5, 7, 17, 257, 65537, …, sont nombres premiers, il me semble que je trouverai de très belles choses en cette matière, car j'ai déjà trouvé des choses merveilleuses dont je vous ferai part ». Ces nombres sont maintenant appelés nombres de Fermat et sa phrase s'avère être l'unique conjecture fausse proposée par l'auteur. René Descartes recherche sans y parvenir, à démontrer que si la division par huit d'un nombre premier donne pour reste un ou trois, il s'écrit de la forme x² + 2y².

Sur ce type de problèmes, deux éléments sont remarquables :

Les équations diophantiennes fascinent, le titre d'un des livres de Bachet de Méziriac est évocateur : Problèmes plaisants et délectables qui se font par les nombres, on peut citer encore la remarque de Fermat à propos de son grand théorème : « J'ai trouvé une solution merveilleuse … »

Les problèmes posés sont difficiles. Malgré quelques succès comme l'identité de Bézout probablement due à Bachet de Méziriac, l'essentiel des questions restent sans réponse, comme le théorème des deux carrés de Fermat, ou avec des réponses pour le moins peu convaincantes, comme celle de Fermat pour son grand théorème :«… mais la place me manque ici pour la développer » (la première preuve reconnue apparaîtra en 1995). Bien souvent, Fermat termine ses théorèmes par des commentaires avouant son échec : « Je vous avoue tout net (car par avance je vous avertis que je ne suis pas capable de m'attribuer plus que je ne sais, je dis avec la même franchise ce que je ne sais pas) que je n'ai pu encore démontrer … cette belle proposition que je vous ai envoyée … »

Méthodes utilisées

Leonhard Euler, théoricien des nombres du XVIII^e siècle, résout plusieurs équations diophantiennes.

Le siècle suivant voit la résolution de certaines de ces questions, souvent par Leonhard Euler : il contredit Fermat en démontrant que ses nombres ne sont pas toujours premiers, et prouve le théorème des deux carrés. Il commet aussi des erreurs, sa tentative de démonstration du grand théorème de Fermat pour n égal à trois est un échec, sa première démonstration s'avère fausse. Il soulève d'autres questions comme la loi de réciprocité quadratique en 1782. Là encore, et malgré une tentative d'Adrien-Marie Legendre, la solution reste hors de portée.

Jusqu'à l'aube du XIX^e siècle les méthodes utilisées, si elles dénotent une grande astuce chez les mathématiciens, sont finalement peu nombreuses et de principes simples. L'exemple suivant, tiré du problème des deux carrés, en illustre trois : existe-t-il un nombre dont la division par quatre donne pour reste 3 et qui est somme de deux carrés ? Soit a² et b² ces deux carrés. Seul l'un est pair car sinon leur somme serait paire et sa division par 4 aurait 0 comme reste. Supposons a pair et b impair. a est pair donc son carré est un multiple de 4. L'entier b est impair donc s'écrit 2c + 1, son carré est égal à 4c² + 4c + 1, la division de b² par quatre donne pour reste un et la somme des deux carrés donne aussi pour reste un.

• Le premier outil utilisé est celui des nombres premiers, ce raisonnement est exact car 2 est un nombre premier.
• Le deuxième est la transformation algébrique, b est transformé en 2c + 1. Utilisé avec virtuosité, il permet aux mathématiciens de l'époque de résoudre certaines équations diophantiennes. Toute l'astuce réside à choisir avec habileté les bonnes transformations.
• Le troisième est la division euclidienne, les carrés et leur somme sont systématiquement divisés par 4.
• Le quatrième n'est pas illustré dans l'exemple, il correspond à la descente infinie utilisée dans la démonstration d'Euler du théorème des deux carrés. Elle consiste à trouver à partir d'une solution entière positive une autre solution entière positive et plus petite. La suite des solutions descend de manière infinie dans l'ensemble des entiers positifs, ce qui n'est pas possible. Cette méthode fut déjà utilisée par Fermat pour démontrer son grand théorème dans le cas où n est égal à 4.

Le caractère rustique des outils se traduit par des démonstrations longues et techniques, comme la preuve d'Euler pour le théorème des deux carrés. De plus, et malgré plus d'un siècle d'efforts, l'essentiel des équations diophantiennes résistent à une telle approche.

L'apport de Carl Friedrich Gauss

Carl Friedrich Gauss est le fondateur de la branche mathématique maintenant appelée arithmétique modulaire.

À l'âge de 17 ans, Gauss démontre la loi de réciprocité quadratique. Un an plus tard, le 30 mars 1796, il prend conscience que ses calculs arithmétiques permettent de construire à la règle et au compas l'heptadécagone, c'est-à-dire le polygone régulier à dix-sept côtés, problème resté ouvert depuis l'Antiquité. Enfin en 1801, il publie Disquisitiones arithmeticae (Recherches arithmétiques) et est surnommé le prince des mathématiciens.

Ces deux grandes découvertes procèdent d'une même démarche, la mise au point d'outils plus sophistiqués que ceux dont disposaient Fermat ou Euler, simplifiant les démonstrations au prix d'une abstraction plus grande. Sa démarche fonde l'arithmétique modulaire.

Elle est appliquée d'abord aux entiers puis aux polynômes puis à un nouvel ensemble d'entiers, maintenant appelés entiers de Gauss.

Toutes les équations diophantiennes de Fermat sont maintenant résolues à l'exception de son grand théorème. De nouvelles conjectures apparaissent. Par exemple, si a et b sont premiers entre eux, la suite arithmétique de valeur initiale a et de raison b contient-elle des nombres premiers, si oui combien ? Gauss et d'autres mathématiciens comme Legendre ont bien imaginé qu'il en existe une infinité mais ne parviennent pas à le démontrer. De même la loi de réciprocité quadratique doit posséder des équivalents pour les ordres supérieurs.

L'arithmétique modulaire est enrichie. Dirichlet, un élève de Gauss trouve une démonstration du théorème de la progression arithmétique en développant le concept des caractères et en formalisant les bases de la théorie analytique des nombres. Charles Gustave Jacob Jacobi écrit, dans une lettre à son frère : « En appliquant les séries de Fourier à la théorie des nombres, Dirichlet a récemment trouvé des résultats atteignant les sommets de la perspicacité humaine. » Dirichlet n'est pas le premier à utiliser des outils qui sont maintenant qualifiés de conséquence de l'analyse harmonique sur un groupe abélien fini. Legendre, pour tenter de démontrer la loi de réciprocité quadratique, développa des calculs similaires sur les réels, formalisant ce qui est maintenant appelé le symbole de Legendre. Gauss enfin généralise cette approche aux nombres complexes dans son livre de 1801. Ses calculs portent le nom de somme de Gauss et période de Gauss.

Au XIX^e siècle, ces mathématiques sont dénommées arithmétique transcendante. Si le terme d'arithmétique reste largement usité, Legendre considère, en 1830, cette branche comme suffisamment développée pour mériter le terme de théorie des nombres. L'apparition de nouvelles techniques, différentes de celles de Gauss, introduit une subdivision avec la théorie algébrique des nombres et la théorie analytique des nombres. Le terme d'arithmétique transcendante tombe ensuite en désuétude.

XX^e siècle

Cryptologie

Auguste Kerckhoffs énonce un principe fondateur de la cryptologie moderne.

Enigma, une machine de chiffrement utilisée durant la Seconde Guerre mondiale, décrypté par un mathématicien : Marian Rejewski.

Ce domaine quitte celui des mathématiques pures. En revanche, une application industrielle fait, au cours du temps, de plus en plus appel aux notions mathématiques développées par Gauss : la science des codes secrets appelée cryptologie. En 1883, Auguste Kerckhoffs énonce que : « la sécurité d'un système de cryptographie ne doit pas reposer sur le secret de l'algorithme. La sécurité ne repose que sur le secret de la clé ». Cette approche est à l'origine d'une modification profonde de cette science. Au milieu du XX^e siècle, elle devient une branche des mathématiques appliquées.

Au début des années 1930, le bureau du chiffre polonais fait appel au mathématicien Marian Rejewski pour percer le code du système Enigma, utilisé par les Allemands. Les anciens codes, comme le chiffre de César, sont réinterprétés comme une transformation mathématique dans l'ensemble des moduli de Gauss sur les nombres entiers. Le terme d'« arithmétique modulaire » est utilisé pour décrire ces techniques. Durant les années 1970, Horst Feistel développe un système à clé privée, le Data Encryption Standard ou DES, qui devient le standard des applications non classifiées. Les cryptanalystes du DES, et plus généralement des chiffrements symétriques, utiliseront des mathématiques issues des travaux de Dirichlet sur les caractères, dans le cadre d'un espace vectoriel sur un corps fini à deux éléments.

En 1976 une nouvelle famille de codes est découverte, fondée sur une clé publique. Des solutions industrielles sont rapidement développées, la plus célèbre est dénommée R.S.A.. Elle se fonde sur les travaux de Fermat et d'Euler. Le terme« arithmétique modulaire » est, dans ce contexte, utilisé pour décrire non seulement la structure des moduli sur les entiers, mais aussi les théorèmes traitant des nombres premiers comme la décomposition en produit de facteurs premiers, le théorème chinois, le petit théorème de Fermat et sa généralisation par Euler.

Avec le développement de l'informatique, l'arithmétique modulaire devient un domaine de recherche actif : les applications nécessitent l'utilisation d'opérations sur des grands nombres, et la mise en œuvre d'algorithmes efficaces.

Théorie de l'information

Un Processeur Pentium contenant une unité arithmétique et logique fondée sur l'arithmétique modulaire.

La cryptographie n'est pas l'unique domaine utilisant le vocable« arithmétique modulaire ». La fin de la Seconde Guerre mondiale voit l'apparition d'une nouvelle science : la théorie de l'information. En 1948, sous l'impulsion de Claude Shannon, elle devient une branche des mathématiques appliquées.

Si la confidentialité est l'un des sujets abordés, la fiabilité est aussi un thème majeur. Richard Hamming propose un premier algorithme dès 1950. Une fois encore, les moduli sur les entiers sont utilisés pour une des plus simples techniques de code : les sommes de contrôle. En 1960, de nouveaux codes plus puissants sont développés, sur la base de polynômes à coefficients dans un corps fini. L'arithmétique utilisée prend souvent le nom de« modulaire ».

L'informatique devient un sujet universitaire au début des années 1960. Les contraintes inhérentes à la structure des processeurs imposent la représentation des nombres sous forme d'une suite finie d'informations, justifiant l'utilisation des moduli. Le terme d'« arithmétique modulaire » apparaît souvent, on y trouve même les entiers de Gauss ou les polynômes, par exemple, pour des calculs sur des grands entiers.

Les techniques développées pour la cryptographie, la théorie des codes et l'arithmétique informatique reposent sur les mêmes concepts, offrant une relative unité aux mathématiques de la théorie de l'information.

Outils de l'arithmétique modulaire

Congruences sur les entiers

L'exemple historique de l'« arithmétique modulaire » repose sur les nombres entiers. Un entier n étant fixé, le calcul modulo n consiste à identifier tous les entiers à leur reste dans la division euclidienne par n ; ceci peut être illustré par l'exemple de l'« arithmétique de l'horloge », qui correspond à n=12 : la petite aiguille se trouve dans la même position à deux moments éloignés de douze heures, on identifie par exemple 13 h à 1 h. Pour obtenir un calcul sur un tel ensemble, on vérifie que l'addition et la multiplication sont compatibles avec les identifications. Cette formalisation est l'œuvre de Legendre, qui donne le nom de résidu aux différents éléments.

L'apport de Gauss consiste à analyser la structure de cet ensemble, maintenant qualifié du nom d'anneau de congruences et noté ℤ/nℤ. Elle se divise en premier lieu en l'étude de l'addition, qui définit un groupe cyclique de générateur 1 ; puis de la multiplication, qui dépend des propriétés du modulo. Si celui-ci est premier, on obtient un corps. Cette approche simplifie les démonstrations arithmétiques. Les deux exemples historiques du livre Disquisitiones arithmeticae sont le théorème de Wilson et le petit théorème de Fermat.

Le calcul modulaire, dans le cas où le modulo n'est pas premier, est plus complexe, mais le théorème des restes chinois permet d'en élucider la structure. L'anneau n'est alors pas intègre et il existe des diviseurs de zéro, ce sont des nombres qui, multipliés par un certain autre nombre non nul, donnent zéro. Le nombre d'éléments inversibles est donné par la fonction indicatrice d'Euler. Elle permet, par exemple, de généraliser le petit théorème de Fermat.

Résidus et polynômes

Figure à la règle et au compas: l'heptadécagone, un polygone régulier de 17 côtés, mis en évidence avec les techniques de l'arithmétique modulaire.

Gauss remarque que l'ensemble des polynômes à coefficients rationnels peut se voir appliquer la logique du calcul modulaire, puisqu'il dispose d'une addition, d'une multiplication, et d'une division euclidienne. Les congruences sont les restes de la division euclidienne des polynômes par un polynôme donné.

Il applique cette approche au polynôme Xⁿ – 1 et trouve sa décomposition en produit de facteurs irréductibles, qui prennent le nom de polynôme cyclotomique. Gauss utilise ces résultats pour trouver une construction à la règle et au compas de l'heptadécagone, polygone régulier à 17 côtés.

Il hésite à considérer ces travaux comme de l'arithmétique ; il écrit :« La théorie de la division du cercle, ou des polygones réguliers…, n'appartient pas par elle-même à l'Arithmétique, mais ses principes ne peuvent être puisés que dans l'Arithmétique transcendante ». La logique de cet argument est toujours d'actualité.

Entiers algébriques

Le cas des polynômes à coefficients entiers diffère : la propriété de division ne fonctionne que pour des polynômes dont le plus grand coefficient est égal à plus ou moins un. Le cas des moduli du polynôme X² + 1 est envisagé : la structure modulaire obtenue est encore celle d'un anneau, s'identifiant à l'ensemble des nombres de la forme α + iβ où α et β sont des entiers et i désigne l'unité imaginaire, correspondant au monôme X. Cet ensemble est celui des entiers de Gauss.

Illustration de la division euclidienne pour les entiers de Gauss

Illustration de la démonstration du théorème des deux carrés par les entiers de Gauss

Il peut être muni d'une norme. À l'entier de Gauss a = α + iβ est associée la norme α² + β², qui provient du module des nombres complexes. Cette norme permet de définir une division euclidienne, comme l'illustre la figure de droite. Les entiers sont représentés par les intersections du quadrillage. La valeur a/b existe si b est différent de zéro, cependant cette valeur n'est pas nécessairement un entier de Gauss. Elle est représentée par le point noir de la figure. Dire qu'une division euclidienne existe, revient à dire qu'il existe un entier de Gauss à une norme strictement inférieure à un de ce point noir. L'illustration montre que, dans le cas présent, il existe au moins trois candidats. Dans le cas général, il en existe entre un et quatre et dans ce contexte seule l'existence compte.

Ce résultat de division euclidienne implique des propriétés sur cet anneau d'entiers : l'identité de Bézout, l'existence de nombres premiers de Gauss et un analogue du théorème fondamental de l'arithmétique. Ces nombres premiers permettent à Richard Dedekind de proposer une résolution simple du théorème des deux carrés. L'illustration géométrique est donnée sur la figure de gauche. Un nombre premier p s'exprime comme somme de deux carrés si le cercle de rayon la racine de p croise au moins un entier Gauss.

Gotthold Eisenstein, qui rencontre Gauss en 1844, découvre un nouvel anneau d'entiers ; l'arithmétique sur cet anneau offre une démonstration rigoureuse du grand théorème de Fermat pour n égal à trois, justifiant, encore une fois, la nécessité théorique d'une telle généralisation de l'arithmétique modulaire.

Caractères de Dirichlet

Peter Dirichlet développe l'essentiel de la théorie dans le cadre de l'anneau ℤ/nℤ.

Dirichlet s'intéresse aux nombres premiers de la forme n + λm où n et m sont deux entiers premiers entre eux et λ une variable qui décrit l'ensemble des entiers positifs. Il souhaite en effet démontrer qu'il existe une infinité de nombres premiers de cette nature.

L'arithmétique modulaire est un bon outil pour cette problématique, qui est équivalente à trouver le cardinal de l'ensemble des nombres premiers dans une classe de modulo.

Dirichlet considère le groupe des éléments inversibles modulo m, et étudie l'ensemble des fonctions du groupe dans les nombres complexes non nuls qui vérifient, pour a et b deux éléments de ce groupe, f(ab) = f(a)f(b). De telles fonctions sont appelées caractères de Dirichlet. Il en existe φ(n), le produit de deux caractères est encore un caractère, et leur table de multiplication est exactement la même que celle du groupe des unités étudié.

Les calculs sur ces fonctions sont formellement analogues à ceux réalisés précédemment par Joseph Fourier. Il faut néanmoins atteindre le XX^e siècle pour voir apparaître une théorie unifiant les deux approches. Elle prend le nom d'analyse harmonique.

Développements théoriques

Il est fréquent que des concepts mathématiques, développés dans un contexte, soient réutilisés dans d'autres domaines. Ainsi la théorie des groupes s'applique à l'arithmétique et à la géométrie. Il en est de même pour les outils de l'arithmétique modulaire, dont les outils alimentent de vastes champs des mathématiques pures, comme l'algèbre générale ou la théorie de Galois. Ces théories ne sont néanmoins pas considérées comme des cas particuliers d'arithmétique modulaire car elles font aussi appel à de nombreux autres concepts.

Structures quotient

En langage moderne, l'arithmétique modulaire se formalise par la notion de quotient d'anneaux euclidiens. Le concept de relation d'équivalence permet de généraliser ce concept aux principales structures algébriques. Par exemple, le quotient d'un groupe par un sous-groupe normal est, à travers le théorème de Jordan-Hölder, un outil de base de la classification des groupes finis. Les groupes quotients sont aussi utilisés en topologie algébrique pour classifier les variétés. Dans la théorie des anneaux, la notion d'idéal joue un rôle analogue à celui de la notion de sous-groupe normal en théorie des groupes. Elle permet de construire des anneaux quotients dans un contexte plus général que celui de l'arithmétique modulaire. Le théorème des zéros de Hilbert, base du lien entre l'algèbre commutative et la géométrie algébrique, s'exprime en termes d'idéal.

Les termes de congruence et de modulo sont néanmoins réservés aux quotients sur un anneau euclidien.

Résidus de polynômes et théorie de Galois

Évariste Galois est le fondateur de la théorie portant maintenant son nom.

Les idées de l'arithmétique modulaire s'appliquent à l'anneau des polynômes à coefficients dans un corps commutatif, car cette structure dispose d'une division. Elle est le point de départ de la théorie d'Évariste Galois et consiste en l'étude systématique des ensembles de congruence de polynômes modulo un polynôme irréductible, l'équivalent des nombres premiers. Ces ensembles sont maintenant appelés extensions algébriques.

Ces extensions permettent l'analyse de la résolubilité des équations algébriques, c'est-à-dire des équations s'écrivant sous forme polynomiale. Si le polynôme est irréductible, son ensemble de congruences est le plus petit corps contenant au moins une racine. Il est appelé corps de rupture. En réitérant ce processus, un corps contenant toutes les racines, le corps de décomposition, est construit. La logique modulaire du quotient fournit la structure algébrique adaptée à cette problématique.

La théorie de Galois fait appel à bien d'autres notions. L'étude de la résolubilité de l'équation est possible via l'étude du groupe des automorphismes du corps, appelé groupe de Galois, grâce à la correspondance de Galois entre sous-corps et sous-groupes. Au-delà de l'étude de la résolubilité des équations algébriques, la théorie de Galois est devenue un cadre naturel de résolution de nombreux problèmes en arithmétique, géométrie arithmétique ou géométrie algébrique, et permet surtout de formuler de nouveaux problèmes plus généraux dans ces divers domaines.

Si cette théorie utilise le concept de quotient d'un anneau euclidien, la variété d'outils spécifiques à ce domaine en fait un champ propre, bien distinct du sujet de cet article. L'un des fruits de cette théorie, les corps finis, encore appelés corps de Galois, fournissent un cadre naturel à de nombreuses applications en arithmétique modulaire.

Entiers algébriques et théorie algébrique des nombres

Ernst Kummer démontre le dernier théorème de Fermat pour de nombreuses valeurs de n et fonde la théorie algébrique des nombres.

L'arithmétique modulaire offre un bon cadre conceptuel pour la résolution du grand théorème de Fermat. Cependant, les anneaux d'entiers algébriques, construits selon la méthode de Gauss, présentent ce que Dirichlet appelle une obstruction. Il montre que le groupe des unités de cet anneau, c'est-à-dire des éléments ayant un inverse pour la multiplication, n'est plus un groupe cyclique ou abélien fini comme celui qu'étudiait Gauss. Il contient aussi des copies de l'anneau des entiers et est donc infini. Ce résultat prend le nom de théorème des unités de Dirichlet. L'obstruction provient de cette nouvelle configuration. Elle empêche l'application des techniques modulaires utilisées pour les entiers de Gauss car l'anneau associé n'est plus euclidien.

Ernst Kummer utilise un outil lié à la généralisation du quotient maintenant formalisé par les idéaux. Ils remplacent les nombres premiers absents. La théorie algébrique des nombres prend alors le relais, avec des techniques différentes. L'outil de base est un anneau dont les éléments sont appelés entiers algébriques et qui possède une structure dite d'anneau de Dedekind. Kummer parvient ainsi à démontrer le grand théorème pour certaines valeurs de n premier, c'est-à-dire pour les nombres premiers réguliers. Les seules valeurs inférieures à 100 non traitées sont 37, 59 et 67.

D'autres outils et objets d'étude apparaissent, comme l'anneau adélique, ceux de la théorie de Galois, les courbes elliptiques, les séries L de Dirichlet ou les formes modulaires. Certains proviennent de conséquences presque directes de l'arithmétique modulaire, comme les corps finis, utilisés de manière intensive au XX^e siècle. La théorie algébrique des nombres est largement plus vaste que le cadre de l'arithmétique modulaire, tout en reposant in fine sur des techniques parfois similaires.

Caractères de Dirichlet et théorie analytique des nombres

Représentation du module de la fonction zêta de Riemann.

Bernhard Riemann émet l'hypothèse de localisation des racines de la fonction ζ (zêta).

La découverte par Euler d'un produit infini, construit à l'aide de nombres premiers et égal à $\pi ^{2}/6$ouvre la voie à une approche différente pour la compréhension des nombres. Dirichlet l'utilise pour démontrer que chacun des moduli d'entiers du groupe des unités contient une infinité de nombres premiers. Ce résultat porte maintenant le nom de théorème de la progression arithmétique.

Pour mener à bien sa démonstration, Dirichlet développe un outil spécifique, les séries L de Dirichlet. L'une de ses séries correspond à une célèbre fonction qui prendra le nom de ζ (zêta) de Riemann. Sa plus grande difficulté consiste à prouver que ses fonctions n'ont pas de racine au point un. Pour y parvenir, il utilise l'analyse harmonique sur le groupe des unités d'une classe de modulo.

Néanmoins, une fois encore, l'arithmétique modulaire est insuffisante pour venir à bout du théorème. Dirichlet utilise de nombreuses techniques analytiques, comme les séries entières et l'analyse complexe. Le fruit de ces travaux donne naissance à une nouvelle branche des mathématiques : la théorie analytique des nombres. L'un des points cruciaux de cette théorie provient de l'unique article de Bernhard Riemann en théorie des nombres : Sur le nombre de nombres premiers inférieurs à une taille donnée. Il conjecture une localisation des racines de sa fonction ζ. La recherche de la position des racines, initiée par Dirichlet, devient une préoccupation centrale et reste l'une des conjectures pressenties comme les plus difficiles des mathématiques de notre époque.

Cryptographie

L'hameçonnage est une technique visant à obtenir des informations confidentielles sur internet en vue d'une escroquerie. La nécessité de communication d'informations confidentielles représente un danger en cryptographie.

L'objet de la cryptographie est d'assurer la sécurité dans la transmission des messages. La confidentialité ainsi que l'authentification de ceux-ci sont deux exemples du sens donné au terme sécurité. On peut citer deux exemples : la protection des messages qu'utilise une armée pour empêcher une anticipation de l'ennemi, ou la carte bleue proposée par le système bancaire, offrant à un usager une bonne sécurité.

En termes plus mathématiques, l'opération de chiffrement se traduit par un algorithme, c'est-à-dire une fonction f qui, à un message en clair m et une clé k, associe un message chiffré f(k, m). La connaissance du message chiffré et de l'algorithme doit être insuffisante pour reconstituer le message en clair sans une clé de déchiffrement. Dans le cas de la cryptographie traditionnelle, dite cryptographie symétrique, la clé de déchiffrement est identique à la clé de chiffrement ou s'en déduit aisément. Cette clé doit alors rester secrète.

La cryptographie asymétrique s'appuie sur le constat que seule la clé de déchiffrement doit rester secrète, et connue du seul récepteur du message. Elle n'a pas besoin d'être communiquée à ses correspondants. Alice utilise la clé de chiffrement de Bob, que celui-ci a rendu publique, pour lui envoyer un message. Seul Bob peut le déchiffrer, même Alice, si jamais elle avait perdu le message en clair, en serait incapable. Bob doit répondre en utilisant la clé de chiffrement d'Alice.

L'objectif est donc de définir une fonction simple à évaluer mais difficile à inverser sans la connaissance d'un secret. L'arithmétique modulaire a été la première à offrir des solutions, et elle est toujours à la base de beaucoup de solutions commerciales. Par exemple l'échange de clés Diffie-Hellman, premier exemple historique, exploite la difficulté pratique à inverser l'exponentiation modulaire. Cette dernière, ou ses généralisations à d'autres groupes, reste fondamentale dans le domaine.

La cryptographie asymétrique résout en particulier le délicat problème de la distribution des clés en cryptographie symétrique. Si plusieurs correspondants communiquent, en cryptographie symétrique, une clé différente s'avère nécessaire pour chaque couple d'intervenants, alors qu'en cryptographie asymétrique chaque correspondant dispose d'une clef qu'il garde secrète, et d'une clef qu'il rend publique. Cependant elle n'a pas fait disparaître les codes symétriques, qui offrent des algorithmes beaucoup plus efficaces. Pour une sécurité équivalente, les codes symétriques présentent l'avantage de nécessiter des clés nettement plus petites, 128 bits pour la version courante de AES, contre plus d'un millier pour le RSA, mais surtout le chiffrement comme le déchiffrement sont de cent à mille fois plus rapide. Les systèmes cryptographiques modernes, comme ceux utilisés par les cartes bancaires, ou le protocole de communication cryptée SSL/TLS très utilisé sur Internet, n'utilisent qu'en début de communication la cryptographie asymétrique, pour échanger les clés d'un chiffrement symétrique qui prendra ensuite le relais.

Cryptographie asymétrique

Le code RSA est un exemple largement répandu de cryptographie asymétrique. Le chiffrement utilise deux clés, une clé publique pour le chiffrement, et une clé privée, pour le déchiffrement. La force d'un tel système réside dans le fait que la connaissance de la clé publique ne permet pas le décryptage. Il se décrit de la manière suivante :

Alice (le choix des prénoms est traditionnel) souhaite pouvoir recevoir des messages de Bob sans qu'Ève puisse les déchiffrer. Alice choisit deux grands nombres premiers p et q, dont elle calcule le produit n = pq, et un entier e, premier avec φ(n) = (p – 1)(q – 1), et strictement inférieur à ce nombre ; la fonction indicatrice d'Euler φ, donne l'ordre du groupe des éléments inversibles de ℤ/nℤ. Le couple (n, e) constitue alors la clé publique d'Alice, c'est-à-dire qu'elle peut être librement accessible, en particulier à Bob qui doit tout de même pouvoir s'assurer que cette clef est bien celle d'Alice.

Parallèlement Alice calcule l'inverse de e modulo n, soit un entier d strictement inférieur à n vérifiant

$de+k\varphi (n)=1$

ce qui se fait de façon efficace par l'algorithme d'Euclide étendu connaissant p et q, donc φ(n). L'entier d constitue la clef privée d'Alice. On montre que la connaissance de d permet de retrouver la factorisation de n de façon efficace, le calcul de d et la factorisation de n sont donc calculatoirement équivalents.

Les messages sont des entiers strictement inférieurs à n, que l'on voit comme des éléments de l'anneau ℤ/nℤ. Si Bob souhaite transmettre le message m à Alice, il transmet la valeur de m^e modulo n. Alice a rendu au préalable publiques les valeurs de n = pq, e et donc la fonction f de chiffrement, qui est ici égale à :

$f(m)\equiv \ m^{e}{\pmod {n}}$

Ève peut connaître e, n et donc f, ces informations sont en effet publiques. En revanche, elle ne peut intercepter les valeurs de p et q qui n'ont jamais été communiquées.

Pour Bob, la fonction de codage est aisée : il s'agit d'une exponentiation modulaire qui se calcule de façon efficace. Pour Alice la lecture l'est aussi pour les mêmes raisons. En effet le théorème d'Euler montre que :

$m\equiv f(m)^{d}{\pmod {n}}$

En revanche Ève ne connaît pas a priori les entiers p et q. Si n est grand (et si les entiers p et q sont bien choisis) il n'existe pas, à ce jour, d'algorithme assez efficace pour la factorisation de n. Plus généralement on ne connait pas de façon efficace de résoudre le problème RSA, qui est celui d'inverser la fonction de chiffrement (dont on ne sait pas s'il est ou non plus facile à résoudre que le problème de la factorisation de n).

Cryptographie symétrique

La cryptographie asymétrique n'existerait pas sans les méthodes issues de l'arithmétique modulaire. Celle-ci ne joue pas le même rôle fondateur en cryptographie symétrique, mais n'en est pas absente pour autant. Les chiffrements symétriques se divisent en deux grandes familles dont l'une, les chiffrements par flot, utilise souvent comme composant de base les suites récurrentes linéaires sur un corps fini (voir ci-dessous) ; l'autre, celle des chiffrements par blocs, comprend entre autres le DES et son successeur, le standard de chiffrement avancé, appelé couramment AES (pour Advanced Encryption Standard). Ces derniers opèrent sur des blocs de données d'une taille fixe comptée en octets, huit pour le DES par exemple. Une suite d'opérations primitives assez simples est appliquée de façon répétée pour coder un bloc. Un octet, ou plus généralement un bloc de n bits, peut être vu comme les coefficients d'un polynôme sur les entiers modulo deux, de degré maximal n – 1. Cela a conduit les cryptologues à s'intéresser à certaines opérations sur les corps finis de caractéristique 2. Ainsi il s'avère que l'opération d'inversion sur le corps fini F_2ⁿ, composée avec une transformation affine, a de bonnes propriétés cryptographiques pour en faire l'une des primitives des chiffrements par blocs. Ceci a été exploité par les auteurs du chiffrement Rijndael, qui est devenu l'AES. La publication officielle de ce dernier par le NIST (agence fédérale américaine) contient d'ailleurs quelques préliminaires mathématiques sur le sujet. Cependant il n'est nul besoin d'algorithmique sur l'arithmétique ou les corps finis pour l'implémentation : ces opérations sont représentées par des tables, comme les opérations analogues du DES obtenues elles de façon beaucoup plus heuristique. Certains cryptologues ont vu une faiblesse potentielle dans la caractérisation trop algébrique de Rijndael, qui le rendrait plus accessible à l'imagination des mathématiciens, ce qui n'a pas empêché son adoption pour l'AES.

Tests de primalité

Les codes RSA utilisent comme clés les nombres premiers p et q du paragraphe précédent. L'usage, pour les trouver, consiste à choisir un nombre presque au hasard, de tester s'il est premier ou non et de recommencer s'il ne l'est pas.

Le crible d'Ératosthène est une méthode rapide pour les petits nombres. Utilisé habilement, 46 tests suffisent pour vérifier la primalité d'un nombre inférieur à 39 000. En revanche, il est inefficace pour une application industrielle employant des nombres qui s'écrivent avec plusieurs centaines de chiffres.

La majorité des tests de l'industrie se fondent sur des variantes du petit théorème de Fermat. Si un nombre p est premier, alors pour tout entier a, a^p est congru à a modulo p. La réciproque est fausse : il existe des nombres non premiers, appelés nombres de Carmichael (par exemple 561 = 3 × 11 × 17), pour lesquels la congruence est vraie pour toute valeur de a. Toutefois, si p n'est ni un nombre de Carmichael, ni un nombre premier, la congruence est fausse pour au moins la moitié des valeurs de a comprises entre un et p. Que la congruence soit vérifiée pour un grand nombre de valeurs de a indique une très forte probabilité de primalité pour p, s'il n'est pas un nombre de Carmichael.

Le test de primalité de Solovay-Strassen et surtout le test de primalité de Miller-Rabin sont deux exemples largement utilisés. Ils se fondent sur une analyse plus poussée du petit théorème de Fermat et n'admettent pas d'analogues aux nombres de Carmichael, ce qui lève l'un des problèmes du test de Fermat. Pour ces deux méthodes, un test de primalité déterministe consiste à vérifier la propriété pour un nombre de valeurs de a garantissant une preuve irréfutable. Le nombre de calculs à effectuer étant rédhibitoire, on se contente d'un test probabiliste. Il consiste à vérifier la congruence sur un ensemble de valeurs de a, choisi pour assurer une probabilité de primalité supérieure à une valeur donnée, souvent égale à 1 – (1/2)¹⁰⁰.

Décomposition en produit de facteurs premiers

La sécurité par l'obscurité n'est pas de mise pour les codes RSA. Il est important de connaître précisément l'état de l'art de la décomposition des entiers en termes de facteurs premiers. Un concours appelé compétition de factorisation RSA fut ouvert jusqu'en mai 2007, proposant un prix pour quiconque capable de factoriser un nombre choisi dans une liste rendue publique.

Le crible d'Ératosthène est un test de primalité qui offre une méthode de décomposition. Mais une fois encore, il n'est pas applicable pour de grands nombres car trop lent.

Les différentes méthodes actuellement utilisées reposent souvent sur les résidus quadratiques. Un diviseur de zéro est un résidu quadratique contenant comme représentants au moins deux carrés parfaits. L'objectif est de trouver ces deux carrés. Cette approche est celle du crible quadratique et du crible algébrique, le plus rapide connu en 2007. On peut encore citer l'algorithme ρ de Pollard qui utilise le paradoxe des anniversaires.

Corps finis

La construction par quotient des corps premiers ℤ/pℤ se généralise à d'autres structures. En informatique, les nombres sont codés sur n bits, c'est-à-dire qu'un nombre correspond à une suite de longueur n composée de 0 et de 1. Une telle suite peut être considérée comme un vecteur d'un espace vectoriel de dimension n sur le corps fini F₂ à deux éléments.

Cette structure est souvent considérée comme l'espace des polynômes à coefficients dans F₂ de degré strictement inférieur à n. Pour garantir la stabilité de la multiplication, cet espace est quotienté par un polynôme de degré n. Quand ce polynôme est irréductible (équivalent de nombre premier), la structure obtenue est le corps fini de cardinal 2ⁿ. Un nombre a modulo 2ⁿ et un polynôme P modulo un polynôme de degré n sont très semblables, ils s'écrivent en effet :

$a\ =\ \sum _{i=0}^{n-1}a_{i}2^{i}\quad et\quad P\ =\ \sum _{i=0}^{n-1}\alpha _{i}X^{i}\quad ,\quad a_{i},\alpha _{i}\in \mathbf {F} _{2}.$

Un exemple d'utilisation est la création d'un générateur de nombres pseudo-aléatoires dans F₂. De tels générateurs sont utilisés par exemple, dans le contexte d'une communication orale par téléphone portable, par le chiffrement de flux A5/1. Celui-ci a pour composants des registres à décalage à rétroaction linéaire, ou LFSR (acronyme de linear feedback shift register). Étant données deux suites finies d'éléments de F₂ de longueur n, une suite de coefficients et une séquence d'initialisation, soient :

$(c_{1},\dots ,c_{n})$ et $(u_{0},\dots ,u_{n-1}).$

Un LFSR fournit une suite pseudo-aléatoire (u_j), obtenue par récurrence linéaire :

$u_{j}\ =\ \sum _{i=1}^{n}c_{i}u_{j-i}\quad (j\geq n).$

La suite des coefficients est souvent fixe. La clé fournit alors la séquence d'initialisation, qui peut être représentée par un entier a modulo 2ⁿ :

$a\ =\ \sum _{i=0}^{n-1}u_{i}2^{i}.$

La suite obtenue est périodique, cependant si la suite des coefficients est bien choisie, la période est très longue : 2ⁿ – 1. Cette situation se produit si le polynôme de rétroaction R, donnée par la formule suivante, est le polynôme minimal d'un élément primitif du groupe cyclique (F_2ⁿ)* :

$R\ =\ 1-\sum _{i=1}^{n}c_{i}X^{i}.$

Analyse harmonique sur un groupe abélien fini

Les idées de Dirichlet s'appliquent sur le système modulaire du paragraphe précédent. Pour l'addition, l'espace vectoriel V précédent est un groupe abélien fini. Les caractères de ce groupe forment une base orthonormale de l'ensemble des fonctions de V dans celui des nombres complexes. Il est à noter que l'ensemble d'arrivée choisi n'est pas toujours celui des complexes mais parfois le corps F₂. Les résultats sont strictement identiques. Une telle structure dispose d'une analyse harmonique. Si l'ensemble d'arrivée est choisi égal à F₂, la transformée de Fourier prend le nom de transformée de Walsh. Cette approche est utilisée à la fois pour les systèmes DES, RSA et certains chiffrements de flux.

Un registre à décalage à rétroaction linéaire est trop aisément déchiffrable. Pour un registre de longueur n, même si la suite engendrée est de période 2ⁿ – 1, l'algorithme de Berlekamp-Massey permet de déterminer celle-ci grâce à la connaissance de 2n valeurs consécutives, avec une complexité quadratique. Ainsi, si la clé est composée de 128 bits, il suffit de 128 × 128 · k = 16 384 · k étapes pour le décrypter, où k est suffisamment « petit » pour que cela représente une sécurité insuffisante. La solution adoptée consiste à utiliser plusieurs registres à décalage. Les différents résultats sont vus comme un élément d'un nouvel espace vectoriel sur F₂. Une fonction booléenne associe à chaque élément de cet espace la valeur un ou zéro. Si une telle fonction est bien choisie, le meilleur algorithme de déchiffrement connu demande de l'ordre de 2ⁿ étapes pour trouver le signal apportant la confusion. La détermination de cette fonction est obtenue à l'aide des outils de l'analyse harmonique.

Pour un code RSA et à la fin du XX^e siècle, la clé est souvent un nombre dépassant 10³⁰⁸. Il est important de disposer d'une multiplication rapide sur les grands moduli. La technique consiste à identifier les moduli aux polynômes sur un corps fini. La multiplication de deux polynômes de degré n est une opération qui, si elle est réalisée de manière naïve, impose une complexité quadratique. Les caractères du groupe additif associés étant orthogonaux, la complexité devient linéaire si une telle base est utilisée. Un calcul plus rapide consiste à réaliser une transformée de Fourier rapide, à multiplier les deux résultats et à opérer la transformée de Fourier inverse. La complexité totale est alors en nlog(n) où log désigne ici le logarithme de base 2.

Codes correcteurs

Les CD utilisent comme code cyclique une variante du code de Reed-Solomon appelée « code C.I.R.C. »

Un code correcteur n'a pas la vocation d'assurer la sécurité, mais la fiabilité de la transmission d'un message. Il permet de restituer le texte original même si une perturbation aléatoire et modérée se produit durant la transmission. Le message « encodé » est transmis sous une forme appelée « mot du code ». Il contient non seulement les informations du message initial mais aussi les redondances permettant la validation d'une bonne communication et parfois la correction automatique d'éventuelles erreurs.

Un mot du code est composée d'une famille de n « lettres » choisies dans un « alphabet », en général binaire. Le cas industriel le plus fréquent est celui du code linéaire, la valeur n est constante pour chaque mot du code et est appelée dimension du code. L'ensemble des mots du code est muni d'une structure d'espace vectoriel de dimension n.

Les codes linéaires utilisent essentiellement l'arithmétique modulaire comme base mathématique. Beaucoup enrichissent la structure d'espace vectoriel par celle d'un anneau de polynômes sur un corps fini. Ce corps est parfois le corps binaire, souvent un corps de cardinal une puissance de deux. On parle alors de code cyclique.

Les codes linéaires sont largement présent dans l'industrie. La télécommunication les utilise pour le téléphone portable ou internet, l'informatique pour notamment la communication entre la mémoire et de processeur, l'audio-visuel pour les disques compacts ou d'autres formats de même nature comme les DVD.^{[réf. nécessaire]}

Somme de contrôle

Code de longueur deux avec une somme de contrôle.

Une somme de contrôle est un code linéaire particulièrement utilisé. Il correspond à un code correcteur dont seule la détection est automatisable, la correction est obtenue par une demande de répétition du message.

Au message initial est ajoutée une information codée sur une lettre. La lettre est choisie de telle manière que la congruence de la somme des lettres du mot du code soit égale à une valeur donnée, souvent zéro. Dans l'exemple illustré sur la figure de droite, le message initial est composé de deux lettres, un mot du code en contient trois, si le message initial est 00, le mot du code transmis est 000, si le message est 01, le mot du code devient 011. Les quatre mots possibles du code sont illustrés par les points verts de la figure.

Si une unique erreur se produit, sur n'importe laquelle des trois lettres du mot du code, le message reçu correspond à un point noir. Le récepteur sait qu'il doit demander le renouvellement de la transmission. Cette configuration est analogue quelle que soit la longueur du mot du code. Une longueur égale à huit est souvent choisie, elle permet la transmission d'un message de sept lettres. Le résultat est identique, chaque mot licite du code ne possède pour voisin que des mots hors du code, une unique erreur durant la transmission est ainsi détectée. En revanche une double anomalie est systématiquement passée sous silence.

Codes cycliques

Illustration d'un code parfait.

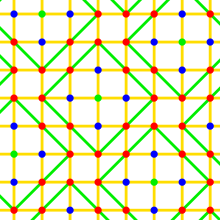
Il existe certaines situations où la demande de répétition n'est pas possible, par exemple pour un DVD, lorsqu'une poussière masque une information. Il est nécessaire d'imaginer des codes correcteurs qui, non seulement détectent, mais corrigent automatiquement les erreurs.

La méthode utilisée consiste à éloigner les mots du code à une distance suffisante pour repérer le bon message d'origine. La distance entre deux points correspond au nombre de lettres à modifier pour passer de l'un à l'autre. Le graphique de gauche illustre cette situation. Les points verts correspondent aux mots du code, par définition sans erreur. Les bleus sont ceux obtenus lorsqu'une unique lettre est altérée dans la transmission et les rouges quand deux lettres sont modifiées. Dans le schéma, on remarque que chaque point bleu contient un unique point vert à une distance de un et à chaque point rouge correspond un unique point vert situé à une distance de deux. Si une ou deux erreurs se sont produites, l'unique point vert le plus proche correspond nécessairement au message initial. Un tel code est capable de protéger jusqu'à deux erreurs.

L'arithmétique modulaire fournit des solutions optimales pour construire la géométrie d'un code linéaire correcteur. Comme un espace vectoriel ne constitue pas une structure suffisante pour définir des moduli, il est enrichi d'une structure d'anneau de polynômes quotienté par Xⁿ - 1, où n désigne la dimension de l'espace vectoriel. Dans cet espace de modulo, le monôme Xⁿ est identifié au polynôme constant un. Si la chaîne (a₀, a₁…, a_n) est un mot du code, alors il en est de même de la suivante : (a_n, a₀, a₁…, a_n-1). On parle pour cette raison de code cyclique. La logique est la même que celle d'un code correcteur, à la différence près que la congruence est définie non pas sur un entier mais sur un polynôme cyclotomique à coefficients dans un corps fini.

L'exemple le plus simple correspond au code de Hamming dont les messages à transmettre comportent quatre lettres et trois lettres supplémentaires décrivent les redondances.

Identité de MacWilliams

Le contexte d'un code linéaire est analogue à celui de la cryptographie, on y trouve aussi des espaces vectoriels de dimension n sur un corps fini et un système de modulo de polynômes, le polynôme choisi étant souvent : Xⁿ + 1. Les caractères du groupe sont utilisés, ainsi que l'analyse harmonique associée.

L'identité de MacWilliams est un exemple archétypal. Elle permet la détermination du polynôme énumérateur des poids du code dual ou encore l'étude des caractéristiques du code de Hamming. Elle est obtenue grâce à l'analyse harmonique, à l'aide d'un produit de convolution.

Notes et références

Liens externes

• Notice dans un dictionnaire ou une encyclopédie généraliste :

  • Britannica
• Quelques phrases extraites de la correspondance de Fermat, sur le site de la commune de Beaumont-de-Lomagne
• Carl Friedrich Gauss. Le Prince des Mathématiciens par Farouk Boucekkine, sur le site CultureMATH
• Arithmétique modulaire et cryptographie, Denis Richard, Université Clermont-Ferrand-I
• Corps finis, Olivier Rioul, ENST
• La cryptologie moderne, Anne Canteaut (Inria) et Françoise Levy-dit-Vehel (ENSTA ParisTech)

Références

• Carl Friedrich Gauss (trad. Antoine Charles Marcelin Poullet-Delisle, éd. Courcier, 1807), Recherches arithmétiques [« Disquisitiones arithmeticae »], 1801
• Jean-Paul Delahaye, Merveilleux nombres premiers : Voyage au cœur de l'arithmétique, 2000 [détail de l’édition]
• Serge Lang, Algèbre [détail des éditions]
• Simon Singh, Le Dernier Théorème de Fermat, Hachette Livre Littérature, 1999 (ISBN 9782709618540)
• Simon Singh, Histoire des codes secrets : de l'Égypte des Pharaons à l'ordinateur quantique, Poche, 2001, 504 p. (ISBN 978-2-253-15097-8)
• Gilles Zémor, Cours de cryptographie, Cassini, 2000 (ISBN 9782842250201)
• Michel Demazure, Cours d'algèbre : primalité, divisibilité, codes [détail des éditions]
• (en) Gavin Flood (en), The Blackwell Companion to Hinduism, Blackwell Publishing, 2005 (ISBN 9781405132510)
• (en) Michael Sean Mahoney, The Mathematical Career of Pierre De Fermat, 1601-1665, Princeton University Press, 2^e éd., 1994 (ISBN 978-0-691-03666-3)
• (en) Waldo Dunnington (de), Carl Friedrich Gauss: Titan of Science, Mathematical Association of America, 2003 (ISBN 0-8838-5547-X)