Grand hexacosichore

Grand hexacosichore
Projection orthogonale
Type	Polychore de Schläfli-Hess
Cellules	600 {3,3}
Faces	1200 {3}
Arêtes	720
Sommets	120
Figure de sommet	{3,5/2}
Symbole de Schläfli	{3,3,5/2}
Diagramme de Coxeter-Dynkin
Groupe de symétrie	H₄, [3,3,5]
Dual	Hécatonicosachore 5/2,3,3
Propriétés	Régulier

En géométrie, le grand hexacosichore, ou hécatonicosachore 3,3,5/2, est un 4-polytope régulier étoilé ayant pour symbole de Schläfli {3,3,5/2}. C'est l'un des 10 polychores de Schläfli-Hess, et le seul possédant 600 cellules.

C'est l'un des quatre 4-polytopes réguliers étoilés découverts par Ludwig Schläfli.

Le grand hexacosichore peut être considéré comme l'analogue quadridimensionnel du grand icosaèdre (qui est à son tour analogue au pentagramme) ; tous deux sont les seuls polytopes réguliers étoilés à n dimensions qui sont dérivés en effectuant des opérations de stellation sur un polytope pentagonal.

Le grand hexacosichore est dual à l'hécatonicosachore 5/2,3,3, analogue de la dualité du grand icosaèdre avec le grand dodécaèdre étoilé.

Polytopes associés

Il a la même disposition d'arêtes (en) que le l'hécatonicosachore 5/2,3,5 et l'hécatonicosachore 5/2,5,5/2, ainsi que la même disposition de faces que l'hécatonicosachore 3,5/2,5.

Projections orthogonales par le plan de Coxeter (en)
H₃	A₂ / B₃ / D₄	A₃ / B₂

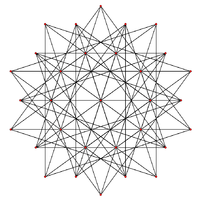
Articles connexes

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Grand 600-cell » (voir la liste des auteurs).

Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [1] .
HSM Coxeter, Polytopes réguliers, 3e. éd., Dover Publications, 1973. (ISBN 0-486-61480-8) .
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, Les symétries des choses 2008, (ISBN 978-1-56881-220-5) (Chapitre 26, Regular Star-polytopes, pp. 404-408)

Portail de la géométrie