Wikipédia

Fond diffus cosmologique

Rayonnement micro-onde omniprésent dans l'Univers ; le plus ancien rayonnement électromagnétique connu de l'Univers
(Redirigé depuis Rayonnement diffus cosmologique)
Page d’aide sur l’homonymie

Ne doit pas être confondu avec Rayonnement de fond. Pour les articles homonymes, consulter FDC Ce lien renvoie vers une page d'homonymie ou CMB Ce lien renvoie vers une page d'homonymie.

Wikipédia:Bons articles

Vous lisez un « bon article » labellisé en 2018.

Le fond diffus cosmologique (FDC, ou CMB pour l'anglais cosmic microwave background, « fond cosmique de micro-ondes ») est un rayonnement électromagnétique très homogène observé dans toutes les directions du ciel et dont le pic d'émission est situé dans le domaine des micro-ondes. On le qualifie de diffus parce qu'il ne provient pas d'une ou plusieurs sources localisées, et de cosmologique parce que, selon l'interprétation qu'on en fait, il est présent dans tout l'Univers (le cosmos).

Carte complète du CMB, selon une projection de Mollweide, méthode qui déroule une sphère sur un plan tout en conservant les surfaces, ce qui « permet de comparer en un coup d'oeil les zones chaudes et les zones froides du ciel »[1]. Cette carte montre les fluctuations ou anisotropies de températures de l'Univers primordial. « Les régions bleues sont les plus froides, alors que les rouges sont les plus chaudes. La différence maximale de température est de l'ordre de 0,000 1 °C[2]. » Ces « légères fluctuations [seraient] le reflet de la première variation de densité à l'origine des galaxies »[3] et des amas de galaxies[4]. Photomontage de clichés pris par WMAP, satellite de la NASA, pendant neuf ans.

Prévu dès 1948 et découvert par hasard en 1964, le fond diffus permet à la communauté scientifique de départager les différents modèles cosmologiques, notamment en abandonnant les modèles fondés sur le principe cosmologique parfait et en donnant la priorité aux modèles basés sur l'idée de Big Bang, qui prédisent l'émission d'un tel rayonnement thermique à l'époque de l'Univers primordial.

Selon le modèle standard de la cosmologie, ce rayonnement a été émis environ 380 000 ans[a] après le Big Bang (ce qui fait qu'on l'appelle aussi rayonnement fossile), alors que l'Univers observable était encore beaucoup plus petit, dense et chaud (de l'ordre de 3 000 K) qu'aujourd'hui. Dilué et refroidi par l'expansion de l'Univers, il possède désormais une température moyenne très basse, de l'ordre de 3 K. Le fond diffus cosmologique est très étudié depuis sa découverte pour deux raisons : il correspond à la plus vieille image électromagnétique qu'il est possible d'obtenir de l'Univers et il présente d'infimes variations de température et d'intensité selon la direction observée, des anisotropies détaillées depuis le début des années 1990 qui permettent de recueillir quantité d'informations sur la structure, l'âge et l'évolution de l'Univers.

Prolégomènes

modifier

« [C'est] la découverte la plus importante du siècle, si ce n'est depuis toujours[6] »

— Stephen Hawking

Selon le modèle du Big Bang, dans les premiers millénaires de son existence, l'Univers est notablement plus petit et comprend un plasma de particules (protons, électrons, photons…). Par la suite, il prend de l'expansion tout en refroidissant. Jusque vers 380 000 ans, les conditions sont telles que tous les photons sont continuellement échangés entre les électrons, ces derniers formant une « mer » d'où les photons ne peuvent s'échapper.

L'Univers, poursuivant son expansion, refroidit encore plus, tout en restant très homogène. Cette diminution de température permet la recombinaison : les électrons et les noyaux atomiques se lient, formant des atomes. La « mer » électronique ayant cessé d'exister, les photons peuvent désormais circuler librement dans l'Univers, devenu « transparent ». Quelle que soit l'époque considérée, ils sont donc partout dans l'Univers, à l'exception des corps célestes constitués de la matière « ordinaire » (planètes, astéroïdes, poussières…) qui sont imperméables aux photons. Pour n'importe quel observateur, un sous-ensemble de ces photons forme une sphère centrée sur lui[7], c'est la surface de dernière diffusion.

À notre époque, ces photons font partie du domaine des micro-ondes du fait de l'expansion de l'Univers qui a étiré leur longueur d'onde. Ensemble, ils constituent le fond diffus cosmologique (ou CMB pour Cosmic microwave background). Les photons présentent des caractéristiques mesurables : énergie et polarisation. Depuis la découverte du CMB dans les années 1960, en raison de limitations technologiques, les scientifiques ont principalement étudié l'énergie des photons du CMB, permettant de vérifier que leur spectre électromagnétique était celui du corps noir à une température témoignant de l'expansion de l'univers.

La communauté scientifique est parvenue à établir, par tâtonnements, études et débats, la nature du CMB et l'histoire de l'Univers grâce à des travaux, commencés au début du XXe siècle, qui se poursuivent aujourd'hui.

Prédiction et découverte

modifier
« Ainsi, le bruit-radio observé par Penzias et Wilson pouvait être décrit par une « température équivalente » de 3,5 kelvins. Cette température était beaucoup plus élevée qu'on ne le prévoyait, mais encore très basse en valeur absolue ; il n'est donc pas surprenant que Penzias et Wilson ruminèrent un moment sur ce résultat avant de le publier. On ne pouvait alors certainement pas imaginer qu'il s'agissait du progrès cosmologique le plus important depuis la découverte du décalage vers le rouge[8]. »
— Steven Weinberg, 1978

Le terme « fond diffus cosmologique » est abrégé en FDC, sigle utilisé en français[9],[10]. Le terme anglais Cosmic Microwave Background Radiation (CMBR) se traduit par « rayonnement du fond (de) micro-ondes cosmique »[b], alors que Cosmic Microwave Background (CMB) se traduit par « fond (de) micro-ondes cosmique »[12],[13]. La littérature scientifique utilise volontiers le sigle CMB[14]. Le terme « fond diffus cosmologique » a plusieurs synonymes.

Article connexe : Liste de synonymes de « fond diffus cosmologique ».

En 1896, Charles Édouard Guillaume écrit que la température de la « radiation des étoiles » est de 5,6 K[15]. En 1926, Arthur Eddington estime la température du rayonnement non thermique des étoiles de la galaxie : « ... par la formule E = σT4, la température effective qui correspond à cette densité est de 3,18° absolu »[trad 1],[16]. En 1938, l'astronome S. W. Adams découvre des raies d'excitation émises par les molécules CN d'étoiles. À cette époque, aucun chercheur n'est capable d'expliquer leur origine. Toutefois, des scientifiques mesurent leur température d'excitation : 2,3 K[17]. En 1946, Robert Dicke prédit que la température du « rayonnement de la matière cosmique » est d'environ 20 K, mais ne mentionne aucun rayonnement de fond[18],[19].

C'est en 1931 que Georges Lemaître énonce sa théorie de l'atome primitif pour décrire l'expansion de l'Univers, affirmant qu'à ses débuts, l'Univers est contenu dans un seul atome « dont le poids atomique est la masse de l'univers entier »[20]. Selon ce modèle, l'Univers, qui est à la fois homogène et isotrope[21],[22],[23],[24], croît de façon exponentielle à partir d'une masse contenant une immense quantité d'énergie. Albert Einstein rejette ce modèle, car il ne croit qu'à un Univers statique[25] ; son influence est telle que les chercheurs rejettent à leur tour l'hypothèse de Lemaître[26]. Pourtant, en 1948, s'appuyant sur les travaux de Lemaître, George Gamow, Ralph Alpher et Robert Herman publient des modèles du Big Bang[27] et prédisent pour la première fois l'existence du fond diffus cosmologique[28],[29],[30]. Dans les articles, les trois scientifiques estiment sa température à 5 K[31],[7]. D'autres scientifiques ont estimé la température moyenne de l'espace intersidéral, mais leurs calculs étaient entachés d'erreurs[32]. Par exemple, Arthur Eddington a calculé une température effective Ce lien renvoie vers une page d'homonymie dont la valeur proche du CMB était une coïncidence : elle correspondait au rayonnement des étoiles de notre galaxie et pas au spectre électromagnétique remplissant l'Univers[33]. Les prédictions de Gamow, Alpher et Herman sont discutées lors de plusieurs congrès en physique de 1948 à 1955, jusqu'à ce que les deux derniers soient embauchés à l’Applied Physics Laboratory (Laboratoire de physique appliquée) de l'université Johns-Hopkins, ce qui met fin à leurs recherches sur le CMB. Ce sujet n'est pas évoqué par la communauté astronomique dominante de cette époque, parce qu'elle n'est pas intriguée par les perspectives de la cosmologie.

L'antenne cornet de Holmdel (en) qui a permis à Penzias et Wilson la découverte du CMB. Les signaux électromagnétiques entrent à la droite, sont concentrés par l'« entonnoir » tout en étant dirigés vers les instruments dans le petit bâtiment à la gauche.

Après étude des raies d'absorption fines du spectre d'étoiles, l'astronome Andrew McKellar écrit en 1941 : « Nous pouvons calculer que la « température rotationnelle » de l'espace interstellaire est de 2 K[trad 2],[34]. » Sans le deviner, il a « découvert l'existence du rayonnement fossile[35]. » En 1955, dans une étude du ciel, Émile Le Roux de l'observatoire de radio de Nançay rapporte un rayonnement de fond presque isotrope à 3 ± 2 K[36],[37]. En 1957, Tigran Shmaonov rapporte que « la température effective absolue de la radioémission de fond... est de 4 ± 3 K »[trad 3],[38]. Il indique que l'intensité du rayonnement est indépendante du temps ou de la direction de l'observation[39]. Dans les années 1960, Iakov Zeldovitch et Robert Dicke prédisent à nouveau l'existence du CMB. Dans un court article publié au printemps 1964, les astrophysiciens Andreï Dorochkevitch et Igor Novikov sont les premiers à annoncer la possibilité de détecter le fond diffus cosmologique[40]. En 1964, David Todd Wilkinson et Peter Roll, collègues de Dicke à l'université de Princeton, commencent à construire un radiomètre selon les plans de Dicke dans le but de détecter le CMB[41].

Toujours en 1964, les physiciens américains Arno Penzias et Robert Woodrow Wilson, travaillant au Bell Labs Holmdel Complex dans le New Jersey, complètent la construction d'un radiomètre de Dicke dans le but d'étudier les phénomènes radioastronomiques et les communications par satellites. Le , ils démontrent sans ambiguïté l'existence du CMB[42], même si l'instrument présente une température de bruit supérieure[c] à 4,2 K, ce qu'ils ignorent[43],. Lors d'une rencontre, les chercheurs de Princeton et des Bell Labs déterminent que le rayonnement du CMB est responsable de l'excédent de température de l'antenne[44]. La découverte de Penzias et Wilson, annoncée en 1965[45], constitue le point culminant de plusieurs années de recherche[46]. Dans l'article, ils expliquent qu'il s'agit d'un « rayonnement électromagnétique diffus isotrope, non polarisé, et sans aucune variation de type saisonnier, en provenance de l'Univers »[27]. Les deux Américains sont récompensés du prix Nobel de physique de 1978 pour leur découverte[42] fortuite[47]. Ce bruit de fond électromagnétique, presque isotrope, n'est pas lié à une étoile, une galaxie ou tout autre corps céleste[48],[49].

L'existence du CMB prête à débats dans les années 1960 parce que quelques partisans de la théorie de l'état stationnaire soutiennent que le CMB est la conséquence de la diffusion de la lumière stellaire issue de lointaines galaxies[50]. Toutefois, dans les années 1970, un consensus émerge : le CMB est un résidu du Big Bang. En effet, des mesures plus précises sur une plus large gamme de fréquences démontrent que son spectre thermique est identique à celui d'un corps noir, ce que la théorie de l'état stationnaire est incapable d'expliquer[51].

Harrison[52], Peebles et Yu[53] et Zeldovitch[54] concluent tous les quatre que l'Univers naissant montrerait de petites inhomogénéités (de l'ordre de 10−4 à 10−5). Rashid Sunyaev calcule plus tard l'empreinte observable (observational imprint) que ces inhomogénéités auraient sur le CMB[55]. Des instruments de mesure de plus en plus précis, installés au sol, permettent de réduire les incertitudes des mesures de l'anisotropie du CMB durant les années 1980. RELIKT-1, expérience soviétique sur l'anisotropie du CMB à bord du satellite Prognoz 9 (lancé le ), réduit la limite supérieure d'incertitude sur les anisotropies à grande échelle. La mission COBE de la NASA démontre hors de tout doute les anisotropies ; les résultats sont publiés en 1992[56],[57]. Respectivement responsable de deux instruments ayant permis cette découverte, George Fitzgerald Smoot et John C. Mather reçoivent le prix Nobel de physique de 2006[58].

Missions d'observations

modifier
« Le rayonnement fossile [...] est fait de tous les photons qui ont été émis lors de la transition opacité-transparence et qui se propagent librement depuis. Ce sont les plus vieux photons de l'univers. Ils ont l'âge de l'univers moins un million d'années. »
Échelles angulaires
Tailles apparentes des corps célestes du Système solaire. La Lune (deux traits en gris) et le Soleil (deux traits en rouge) sont presque de la même taille apparente. Pour une représentation relativement juste des tailles, observez cette illustration à 103 fois le diamètre maximal de la Lune. Par exemple, si le plus grand cercle mesure 5 cm sur votre écran, observez l'illustration à 5,15 m de celui-ci.

Lorsqu'ils présentent leurs travaux sur le CMB, les scientifiques préfèrent indiquer une taille apparente ou une échelle angulaire. Il existe en effet une « relation distance-diamètre angulaire » qui est « une simple relation trigonométrique dans l'espace courbe ». De la sorte, ils s'affranchissent de l'obligation de préciser s'il s'agit d'une longueur propre (qui varie en fonction de l'expansion de l'Univers) ou d'une longueur comobile (qui est insensible à l'expansion de l'Univers)[60]. Dans le ciel terrestre, les galaxies occupent moins d'une minute d'arc (1′), les amas de galaxies occupent quelques minutes d'arc et les superamas de galaxies, « moins de 1° »[61]. La Lune a un diamètre moyen apparent de 31 minutes (31′)[62]. Au plus près de la Terre, son diamètre peut atteindre jusqu'à 33 minutes d'arc.

Par ailleurs, les scientifiques classent les mesures angulaires dans trois catégories : petites, intermédiaires et grandes échelles angulaires. Les mesures effectuées sur des phénomènes d'une minute d'arc ou moins sont dites à petites échelles. Si les mesures se rapportent à des phénomènes entre une minute d'arc et un degré, elles sont dites à échelles intermédiaires. Si la taille dépasse le degré, elles sont dites à grandes échelles[63].
 

À la suite de la découverte du CMB, des centaines d'études ont été menées pour le caractériser[64]. Par exemple, une collaboration italo-américaine, commencée en 1979 et poursuivie au moins jusqu'en 1984, confirme que le CMB se comporte comme un corps noir[65] ; « [peu] de temps après », une collaboration de l'ESO et du MIT confirme que le CMB est issu d'un phénomène cosmologique et non pas d'un objet céleste[66]. La mission Cosmic Background Explorer (COBE) de la NASA, menée de 1989 à 1996, détecte et quantifie les anisotropies à grande échelle[67].

Améliorations successives des observations des anisotropies (ou fluctuations) du CMB. De haut en bas[d] :
1. Découverte du CMB en 1964, qui apparaît parfaitement uniforme (à d'éventuelles contributions d'avant-plan dues à la Voie Lactée) ;
2. Carte des anisotropies dressée à partir des mesures du satellite COBE (1992) ;
3. Carte des anisotropies dressée à partir des mesures du satellite WMAP (2003).

Dans les années 1990, parce que les mesures à grande échelle ne peuvent mettre en évidence les irrégularités du fond diffus, une série d'expériences est menée à partir du sol terrestre ou à bord de ballons stratosphériques pour mesurer les anisotropies à petites échelles angulaires. Leur but premier est d'établir l'échelle angulaire du premier pic de pression[e] ou pic acoustique (apparu lorsque la densité de l'Univers primordial a subi de grandes variations, causées par des instabilités gravitationnelles, qui ont induit des oscillations acoustiques dans le plasma[69] ; voir infra pour plus de détails). Le premier pic aurait été détecté lors de l'expérience Toco, résultat confirmé par les études BOOMERanG et MAXIMA[70],[71],[72]. Un second pic aurait été détecté par d'autres expériences, dont WMAP qui confirme hors de tout doute son existence (il aurait aussi détecté le troisième pic)[73].

Dans les années 2000 et 2010, plusieurs expériences sont conduites pour améliorer les mesures de la polarisation gravitationnelle et la résolution angulaire, dont BICEP2[74], BOOMERanG[75], DASI[76], l'observatoire spatial Planck[77], QUaD[78], le South Pole Telescope[79], le télescope cosmologique d'Atacama[80], le télescope QUIET[81] et WMAP[82].

Comparaison de la résolution des cartes du CMB dressées à l'aide des instruments des satellites COBE, WMAP et Planck.

En , la NASA met en orbite une seconde mission d'étude du CMB, WMAP, dans le but de recueillir des mesures plus précises des anisotropies à grande échelle. Publiées en 2003, les premières mesures du spectre de puissance angulaire sont précises à moins d'un degré, ce qui permet d'éliminer plusieurs perturbations cosmologiques. Généralement, les résultats sont en accord avec la théorie de l'inflation cosmique et d'autres théories concurrentes[83]. Même si des expériences au sol permettent de mesurer les fluctuations, leur résolution est moindre parce que « la tiédeur de l'atmosphère terrestre crée un bruit parasite redoutable[84] ».

En mai 2009, l'Agence spatiale européenne lance l'observatoire spatial Planck dans le but d'améliorer la résolution de ces mesures ; cette mission d'étude se poursuit jusqu'en [85]. Grâce à des radiomètres à transistors HEMT (qui peuvent opérer jusqu'aux fréquences millimétriques[86] et qui sont sept fois plus sensibles que les meilleurs transistors contemporains[87]) et des bolomètres sensibles aux bandes de fréquences centrées sur 100, 143, 217, 353, 545 et 857 GHz[88], Planck peut observer le CMB avec une meilleure résolution que WMAP. Ses instruments ont été auparavant testés en Antarctique sur le site du télescope Viper où ils formaient une partie de l'instrument ACBAR[89] — expérience qui a permis de mesurer les anisotropies à petites échelles angulaires avec une précision inégalée[90] — et lors de l'expérience Archeops (l'instrument était monté dans un ballon stratosphérique)[91].

En , l'équipe responsable du satellite Planck publie des cartes du CMB, dont une sur les écarts de température à la moyenne, une autre sur la répartition des masses et une troisième sur les « anomalies de température »[92],[93]. Selon ces modèles, l'Univers serait un peu plus âgé que la valeur couramment admise. Le CMB aurait été le siège de minuscules variations de température lorsque l'Univers était âgé de 370 000 ans. Ces marques reflètent les ondulations de l'Univers à peine âgé d'un milliardième de seconde. Les ondulations seraient à la source de la formation des grandes structures de la toile cosmique : amas de galaxies et matière noire. Selon ces modélisations de 2013, l'Univers est composé de 4,9 % de matière ordinaire, 26,8 % de matière noire et 68,3 % d'énergie noire[94],[f]. En février 2015, la mission Planck publie de nouveaux résultats. Selon ceux-ci, l'Univers serait âgé de 13,799 ± 0,021 milliards d'années et la constante de Hubble serait de 67,74 ± 0,46 km/s/Mpc[95].

Avec Planck, la mesure des fluctuations du fonds diffus n'est plus limitée par la sensibilité de ses détecteurs, mais par la capacité de distinguer ce fond diffus des émissions d'avant-plan des galaxies. Il est donc équipé d'instruments de mesure du fond et d'instruments pour détecter ces avant-plans[96].

La mission Planck est officiellement terminée en juillet 2018, aucune mission de cette envergure n'est prévue dans un avenir proche et des scientifiques croient qu'aucune information supplémentaire pertinente ne peut être tirée des données de Planck. Toutefois, des scientifiques poursuivent certaines recherches : mesures de la polarisation électromagnétique du CMB (ce qui permettrait de trouver une signature de l'inflation cosmique) et analyse de l'influence des grandes structures cosmiques sur sa température et sa polarisation électromagnétique (ce qui revient à étudier les effets des lentilles gravitationnelles)[97].

Caractéristiques

modifier
« [...] le signal apparaît très homogène dans tout le ciel. Les spécialistes disent qu’il se comporte de manière "isotrope". Son intensité reste constante, quelle que soit la direction de visée. On peut en déduire qu’il puise sa source dans les régions les plus reculées. Il nous informe sur le passé lointain du cosmos. Ce brouhaha extraterrestre ne saurait avoir une quelconque origine proche ou locale (Système solaire, Voie lactée…)[98]. »
Graphique du spectre du CMB mesuré par l'instrument FIRAS du satellite COBE en 1999. À cette date, il s'agit du phénomène naturel qui épouse le mieux la forme de la courbe de rayonnement du corps noir[99]. Les barres d'erreur, et donc l'incertitude sur les mesures, sont si petites qu'il est impossible de les distinguer, même à résolution plus élevée. Il est donc impossible de distinguer les données observées (croix rouges) de la courbe théorique (en vert). « Cette figure constitue peut-être le meilleur appui à la théorie du big bang[100]. »

Les recherches ont permis d'établir que le fond diffus cosmologique est doté de deux « caractéristiques physiques principales : propriétés thermiques et isotropie »[101]. Le CMB apparaît comme un corps noir parfait dans la limite de la précision des instruments de mesure, quelle que soit la région du ciel observée[102],[103]. Entre 1965 et 1978, l'intensité du rayonnement est mesurée sur plus d'une douzaine de longueurs d'onde entre 73,5 et 0,33 cm ; « chacune de ces mesures est en accord avec la distribution de Planck de l'énergie selon la longueur d'onde, à une température comprise entre 2,7 et 3 K »[104]. Si la température absolue n'est déterminée qu'avec une précision de 0,1 %, la forme du CMB et sa concordance avec celui d'un corps noir sont déterminées avec une précision bien plus grande grâce à l'instrument FIRAS du satellite COBE ; l'instrument a déterminé le plus précisément cette température : 2,728 ± 0,002 K, et a quantifié l'absence d'écart entre le spectre observé et celui d'un corps noir[105]. Ce rayonnement est isotrope à environ une partie pour 100 000[106],[107]. La mesure du spectre électromagnétique du CMB est la plus précise de tous les corps noirs naturels connus[99].

Le CMB contient la majorité de l'énergie de rayonnement de l'Univers[108], laquelle représente environ 6 × 10−5 fois la densité énergétique de l'Univers[109]. La densité d'énergie du CMB est de 0,25 eV/cm3[110] (4,005 × 10−14 J/m3), alors que sa densité photonique est de 400-500 photons/cm3[111].

Le CMB montre une grande uniformité à grande échelle, quelle que soit la direction selon laquelle on l'observe[112],[113],[114]. Toutefois, lorsqu'il est observé à une petite échelle, il présente d'infimes écarts de température en fonction de la direction d'observation, écarts qui sont aussi appelés fluctuations, anisotropies ou inhomogénéités[96] du CMB. Depuis les années 1990, l'essentiel des recherches porte sur la caractérisation de ces anisotropies[99]. Si elles sont causées par les effets de la surface de dernière diffusion, elles sont qualifiées de « primaires » (ou « intrinsèques »[115]). Si elles sont causées par les interactions du rayonnement avec des gaz chauds ou des puits gravitationnels, interactions qui surviennent après le contact avec la surface de dernière diffusion, mais avant que le rayonnement n'atteigne un observateur, elles sont dites « secondaires »[116].

Anisotropies primaires

modifier
« Ce qui fait de la dépendance directionnelle du fond de rayonnement millimétrique un sujet d'étude passionnant, c'est que l'intensité de ce rayonnement ne doit pas être parfaitement isotrope. Il peut se produire des fluctuations d'intensité accompagnées de petites variations directionnelles provoquées par le caractère « grumeleux » de l'univers au moment où le rayonnement fut émis, ou depuis lors[117]. »
— Steven Weinberg, 1978
Graphique comprenant une courbe complexe et des barres d'erreur.
Spectre de puissance du CMB en fonction de l'échelle angulaire (ou du développement multipolaire), telle que mesuré par cinq missions d'observations. La précision de WMAP (en noir) excède régulièrement celle des quatre autres missions (ACBAR, BOOMERanG, CBI et VSA). L'amortissement par diffusion atténue la puissance dans l'intervalle l ≳ 1000[118]. La bande rouge « délimite la variance cosmique du modèle »[trad 4],[120].
Le pic le plus important, vis-à-vis 1°, correspond aux taches « engendrées par des ondes sonores se propageant à travers le plasma cosmique quasiment à la vitesse de la lumière ». Ce plasma a existé pendant environ 400 000 ans. Ces taches forment aujourd'hui des bulles d'une taille d'environ 400 000 années-lumière après 14 milliards d'années d'expansion de l'Univers. Ces bulles occupent un angle d'environ 1° dans le ciel[121].
« Le spectre des ondes sonores [...] nous apprend que l'espace cosmique ne semble posséder aucune courbure (il est quasiment plat) dans ses trois dimensions. Il nous renseigne également sur la densité de matière sombre et d'énergie sombre dans l'Univers [La] quantité de matière dite « ordinaire » (composée de protons, d'électrons et de neutrons) ne représente que 5 % de la densité de l'Univers. Le reste n'émet pas de lumière, mais se manifeste indirectement par son champ de gravité, qui perturbe le mouvement des astres[122]. »

La structure des anisotropies primaires du CMB est la conséquence de deux effets, principalement : oscillations acoustiques baryoniques et amortissement par diffusion. Les oscillations sont à leur tour la conséquence des interactions entre les photons et les baryons dans le plasma de l'Univers primordial. La pression exercée par les photons tend à éliminer les anisotropies, alors que l'attraction gravitationnelle amène les baryons, qui se déplacent beaucoup plus lentement, à former des masses de densités variables. Ces deux effets antagonistes créent des oscillations acoustiques, créant les pics caractéristiques du CMB. Ces pics, de façon grossière, se forment là où les oscillations acoustiques résonnent, endroits où les photons se découplent quand la résonance atteint un certain mode vibratoire.

L'échelle angulaire du premier pic indique la courbure de l'Univers (mais pas sa topologie), ainsi que sa densité d'énergie[96]. Le prochain pic — rapport des pics impairs aux pics pairs — détermine la densité réduite de baryons[123]. Le troisième pic peut servir à calculer la densité de la matière noire[124]. Les régions où se trouvent les pics donnent également des informations sur la nature de la densité des perturbations premières. Il existe deux types de densités de perturbations : « adiabatique » et « isocourbure »[125] (voir l'article Fluctuation primordiale de densité). Une densité de perturbation générale est un mélange de ces deux types. Les théories qui tentent d'expliquer le spectre de la densité des perturbations premières prédisent des mélanges différents :

  • densité de perturbations adiabatique : chaque type de particule (baryons, photons...) apporte la même densité de perturbations. Par exemple, si à un endroit, la densité des baryons est 1 % plus élevée que la moyenne de l'ensemble, alors les photons apportent aussi 1 % supplémentaire, de même pour les neutrons. L'inflation cosmique prédit que les perturbations primaires sont adiabatiques ;
  • densité de perturbations isocourbures : la somme des densités de perturbations de chaque particule égale zéro. Si à un certain endroit, les baryons apportent 1 % d'énergie de plus que la moyenne de l'ensemble, que les photons apportent aussi la même énergie supplémentaire, et que les neutrinos apportent 2 % moins d'énergie, alors il s'agit de perturbations isocourbures. Les cordes cosmiques produiraient des perturbations primaires isocourbures.

Le spectre du CMB permet de distinguer entre ces deux types parce qu'ils produisent des pics en des lieux différents. Les densités de perturbations isocourbures produisent des pics dont les échelles angulaires sont dans les rapports 1:3:5:..., alors que les densités de perturbations adiabatiques produisent des pics dans les rapports 1:2:3[126]. Les observations permettent de conclure que les densités de perturbations primaires sont entièrement adiabatiques, ce qui est un argument fort en faveur de l'inflation cosmique, éliminant du coup plusieurs autres modèles.

La disparition graduelle du plasma, pendant l'inflation cosmique, atténue l'amortissement par diffusion tout en amplifiant l'amortissement sans collision. Deux phénomènes sont à la source de ce second amortissement :

Ces deux phénomènes contribuent à parts égales à la suppression des anisotropies à petites échelles et donnent lieu à l'amortissement caractéristique des anisotropies à très petite échelle angulaire.

Le découplage des photons et des baryons n'est pas instantané, il arrive lorsque l'Univers atteint un certain âge ; c'est la raison pour laquelle la profondeur de la surface de dernière diffusion est finie. Une méthode pour quantifier la durée du processus de découplage s'appuie sur la fonction de visibilité du photon (photon visibility function, PVF). La fonction P(t) définit la probabilité qu'un photon a diffusé entre les moments t et t + dt. Le maximum de la PVF (c'est-à-dire le moment où un photon du CMB a diffusé pour la dernière fois avec la plus haute probabilité) est connu avec précision. Les résultats tirés des observations du WMAP permettent de calculer le maximum de P(t) à 372 000 ans[127]. Cet âge est régulièrement utilisé comme celui où le CMB a été formé. Toutefois, le découplage des photons et des baryons n'a pas été instantané, il faut donc calculer un intervalle de confiance raisonnable. L'équipe du WMAP a calculé que le PVF est plus grand que la moitié de sa valeur maximale pendant 115 000 ans. Donc, le découplage dure 115 000 ans et se termine lorsque l'Univers atteint 487 000 ans.

Anisotropies tardives

modifier
« L'importance du FDC est fondamentale. En premier lieu, sa nature cosmologique proprement dite apporte des indices en faveur de l'homogénéité et de l'isotropie de l'univers. Et elle indique que ce dernier est passé par un état dense et chaud. Donc, globalement, il permet de confirmer les modèles de big bang, en rendant inaptes les modèles, ou tentatives de modèles, concurrents. [...] Ce rayonnement date de l'époque de la recombinaison, c'est-à-dire un passé très reculé. Il nous renseigne donc sur la physique se déroulant à cet instant, sur l'univers primordial, en particulier sur les fluctuations présentes alors [...] Enfin, il joue le rôle d'une source lumineuse lointaine devant laquelle se profilent tous les objets plus rapprochés, plus récents. L'interaction avec ces objets astronomiques [...] modifie localement ses propriétés. Ainsi l'analyse de ces modifications nous renseigne sur l'univers entre la recombinaison et notre époque[128]. »
— Lachièze-Rey et Gunzig, 1995

Depuis son apparition, des processus physiques ont modifié la structure du fond diffus ; ils sont regroupés sous le vocable d'« anisotropies tardives » ou d'« anisotropies secondaires ». Lorsque ses photons ont commencé à voyager librement, la matière ordinaire était pour l'essentiel composée d'atomes d'hydrogène et d'hélium, tous deux électriquement neutres. Toutefois, les observations actuelles démontrent que la majeure partie de l'espace intersidéral est surtout composée de matière ionisée. Puisque les atomes d'hydrogène neutres ne sont plus aussi abondants, il faut conclure qu'un phénomène a sensiblement altéré les atomes d'hydrogène : c'est la réionisation[129],[130].

Les photons de l'Univers primordial ont été diffusés par des charges électriques libres, tels les électrons. Dans l'Univers ionisé, les ultraviolets ont libéré ces particules des atomes neutres. Aujourd'hui, dans l'ensemble de l'Univers, la densité des particules chargées est si faible qu'elle n'influence pas le fond diffus. Néanmoins si le milieu interstellaire a été ionisé à l'époque de l'Univers primordial, quand il était plus dense, le fond a subi deux effets :

  1. Les petites anisotropies ont été gommées (grosso modo de la même façon qu'un brouillard estompe les détails des objets qu'il enveloppe) ;
  2. La physique des photons diffusés par les électrons induit des anisotropies polarisées sur de grandes échelles angulaires. Cette polarisation angulaire est corrélée à la perturbation de la température grand angle.

Ces deux effets ont été mis en lumière par le Wilkinson Microwave Anisotropy Probe (un observatoire spatial), ce qui démontre que l'Univers était ionisé dans son très jeune âge. Les scientifiques débattent encore (dans les années 2010) sur la source de ce processus hâtif d'ionisation. Elle se trouverait peut-être dans la lumière issue des toutes premières étoiles (population III), de la lumière issue des supernovæ quand elles ont atteint leur fin de vie ou de radiations ionisantes produites lors de l'accrétion de trous noirs supermassifs.

Ultérieurement, la signature du fond diffus cosmologique a été influencée par deux effets arrivés entre la recombinaison et les observations contemporaines : l'effet Sunyaev-Zel'dovich (des électrons très énergétiques diffusent la lumière, transmettant une partie de leur énergie aux photons diffus)[131] et l'effet Sachs-Wolfe (un champ gravitationnel fait décaler vers le rouge ou vers le bleu les photons diffus)[132].

Polarisation des ondes gravitationnelles et effets gravitationnels

modifier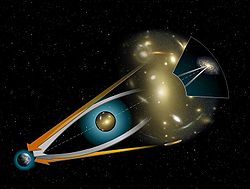
« Le fond diffus cosmologique est un élément essentiel de la cosmologie théorique et observationnelle, un des fondements des modèles du big-bang [...] C'est en effet sa découverte [...] qui a entraîné, à la fin des années 1960, une très large adhésion à ces modèles dont l'idée remontait pourtant à Georges Lemaître en 1931 [...] Comment, par exemple, se sont formées les galaxies et les autres structures cosmiques que nous observons aujourd'hui ? Il s'est avéré que les propriétés du rayonnement diffus cosmologique étaient tout à fait cruciales vis-à-vis de cette question fondamentale[133]. »
— Lachièze-Rey et Gunzig, 1995
Cette vue d'artiste montre sommairement la façon dont la lumière de l'Univers jeune est déviée par la lentille gravitationnelle d'une structure cosmique massive, qui est le siège des modes B.

Puisque l'Univers primordial est opaque jusqu'à la recombinaison, il est en théorie futile d'y rechercher des informations de nature électromagnétique[134],[135]. Néanmoins, des scientifiques ont spéculé sur la possibilité d'une polarisation électromagnétique. Des mesures confirment que dans l'infrarouge, le spectre électromagnétique du CMB ne présente aucune polarisation[136]. Il est toutefois sensible à la gravitation.

La relativité générale d'Albert Einstein a recours aux techniques du calcul tensoriel pour étudier les ondes gravitationnelles (OG)[137]. Une onde électromagnétique (OÉ) est le siège de deux champs : magnétique (représenté par le vecteur ) et électrique (représenté par le vecteur )[138]. Puisque les OG, comme les OÉ, sont susceptibles d'être polarisées, des scientifiques ont créé des quantités tensorielles associées aux OG, qu'ils ont nommées « modes B » et « modes E » par analogie[139]. Dans les OÉ, les champs magnétique et électrique oscillent selon certains motifs (linéaire, circulaire ou elliptique)[140] ; dans les OG, ce sont les modes B et E qui oscillent[139].

Pour ce qui concerne les effets gravitationnels sur l'observation du CMB électromagnétique, le Degree Angular Scale Interferometer (DASI) détecte le premier, en 2002, la polarisation gravitationnelle du CMB[76],[141] — une conséquence naturelle de la diffusion Thomson dans un plasma hétérogène. Le Cosmic Background Imager (CBI) confirme l'existence des modes E de la polarisation gravitationnelle[142]. Ces mesures démontrent que la géométrie de l'Univers est presque plate (c'est-à-dire presque euclidienne), plutôt que courbée (qui obéirait donc aux lois de la géométrie riemannienne, par exemple)[143]. Elles permettent de conclure à l'absence de cordes cosmiques en tant que composantes majeures de la structure cosmique, et suggèrent que l'inflation cosmique explique mieux la formation de cette structure[144].

Dans le CMB, la détection des modes B est extrêmement difficile, parce que le degré de pollution est inconnu, et que des lentilles gravitationnelles faibles mélangent les modes E (qui présentent une signature forte) avec les modes B (qui présentent une signature faible)[145]. Les modes B sont causés par l'influence des lentilles gravitationnelles sur les modes E[146],[147] et par les ondes gravitationnelles issues de l'inflation cosmique. Les cosmologues prédisent deux types de modes B. Le premier apparaît lors de l'inflation cosmique, un peu après le Big Bang[148],[149],[150], alors que le second est la conséquence de lentilles gravitationnelles apparues plus tard[151]. Les ondes gravitationnelles primaires, apparues dans l'Univers primordial, ont pu être observées dans la polarisation du CMB. Les modèles de l'inflation cosmique prédisent leur existence ; leur découverte soutient donc cette théorie (leur intensité permettra de départager ces modèles). Elles sont la conséquence de trois phénomènes : inflation de l'espace même, nouveau réchauffement après l'inflation, et mélange turbulent des fluides de matières et de rayonnements[152]. La polarisation modes B a aussi été observée en octobre 2013 par le South Pole Telescope et le télescope spatial Herschel[147], ce que confirme l'étude de données (2015) issues de l'observatoire Planck[153]. Ces mesures pourraient aider à vérifier les théories sur l'origine de l'Univers[154],[155],[156]. En octobre 2014, l'équipe de l'expérience Polarbear publie une étude des modes B à 150 GHz[157]. Rapportant un niveau de confiance de 97,2 %, elle affirme qu'elles sont d'origine cosmologique[158] (et non pas une conséquence de la poussière interstellaire[159],[160]).

Dipôle de température

modifier
« Ses caractéristiques permettent de retracer l'histoire des premiers instants de l'Univers, bouleversés de réactions nucléaires qui, en un quart d'heure, ont transformé 25 % de la matière en hélium. »
— J. Heidmann, 1968[48]
Observations du CMB par le satellite COBE
Les mesures sont polluées par des effets locaux qui masquent les structures fines du fond diffus cosmologique. L'influence la plus significative provient du dipôle de température, effet causé par les courses de la Terre et du Système solaire dans l'espace. Ces mesures sont aussi polluées par les émissions de micro-ondes provenant entre autres du plan galactique, pollution devant être nettoyée pour révéler la structure du CMB. De plus, les émissions électromagnétiques des galaxies et des nébuleuses doivent être soustraites, ce qui rend incomplètes les cartes du CMB[161].

La première image, résultat des observations du satellite COBE, montre le dipôle de température (dû à la fois aux décalages vers le rouge et vers le bleu) et une partie des étoiles de la Voie lactée[161].

Dans la deuxième image, l'effet du dipôle est supprimé, mais l'effet des étoiles de la Voie lactée, qui apparaît sous la forme d'une bande lumineuse dans le ciel de la Terre, est toujours présent[161].

La dernière image montre le CMB lorsque les effets du dipôle et des étoiles de la Voie lactée sont supprimés[161].

Une fois nettoyées, ces mesures permettent de produire des cartes montrant le spectre de puissance angulaire. Les scientifiques ont recours aux ordinateurs et à la transformation de Fourier pour les créer, décomposant ainsi ces cartes célestes en harmoniques sphériques[162]. Le résultat, obtenu en appliquant la méthode de Monte-Carlo par chaînes de Markov, permet de restreindre plusieurs paramètres cosmologiques.

Du fait de la course de la Terre dans le Système solaire, et plus généralement du déplacement de ce dernier par rapport à la surface d'émission du CMB, la température du fond diffus cosmologique présente une variation en fonction de la direction[163]. Ces déplacements créent donc, par effet Doppler, à la fois un décalage vers le bleu dans la direction du déplacement et un décalage vers le rouge dans la direction opposée[164]. Ce dipôle de température modifie les lectures du CMB[165]. L'effet Doppler permet de calculer une vitesse à partir de cette différence de température. Le Groupe local (dans lequel se trouve la Voie lactée) se déplace à la vitesse de 627 ± 22 km/s relativement au CMB même (qui est donc considéré comme un référentiel cosmologique[48]) dans la direction de la longitude galactique l = 276 ± 3°, b = 30 ± 3°[166],[167],[168].

Autres anomalies

modifier
« Ainsi la surface de dernière diffusion constitue, de beaucoup, le système le plus étendu, le plus éloigné, et le plus homogène que nous connaissions, davantage que l'ensemble de toutes les galaxies ou de tous les quasars connus. [...] Cette surface représente la matière la plus ancienne que nous puissions explorer (c'est l'intérêt principal du [CMB]). Elle constitue l'objet de plus grande dimension possible accessible à nos observations. [... le CMB] constitue un système cinématique de référence meilleur que les étoiles lointaines ; meilleur encore que les galaxies ou les quasars les plus éloignés. [...] Cette surface de dernière diffusion, la plus grande région d'Univers observable, nous offre également la meilleure possibilité de tester l'homogénéité de l'Univers[169]. »
— Lachièze-Rey et Gunzig, 1995

Les données de WMAP étant plus précises que les données antérieures, des chercheurs ont avancé que le CMB montre des anomalies, que ce soit un alignement inexplicable de pôles électromagnétiques, des anomalies à très grande échelle ou une distribution non gaussienne[170],[171],[172]. Historiquement, les scientifiques privilégient la décomposition des anisotropies en harmoniques sphériques[173]. « Les termes d'ordre le plus bas dans ce développement en modes, le dipôle (l = 1) et le quadrupôle (l = 2), sont traités à part » parce que le premier a été détecté le premier et qu'il est nettement plus intense que les autres pôles ; les deux sont une conséquence de l'effet Doppler dû à la course du Système solaire par rapport au CMB. Dans la direction de déplacement de la Terre, qui provoque un décalage vers le bleu, le dipôle apparaît ; le quadrupôle, conséquence d'un effet relativiste, est d'une intensité 100 fois moindre[174],[g].

Une longue controverse concerne les pôles électromagnétiques. Dès la publication d'une carte du CMB à partir des données de COBE, des chercheurs notent que le quadrupôle électromagnétique (l = 2 en harmoniques sphériques) montre une faible amplitude, comparativement aux prédictions du modèle du Big Bang. De plus, le quadrupôle et l'octupôle électromagnétiques (l = 3) semblent alignés, de façon inexplicable, à la fois entre eux, avec le plan écliptique et les équinoxes[175],[176],[177]. Après une analyse minutieuse des calculs, des chercheurs affirment que l'alignement serait moindre, d'environ 5 %[178],[179],[180],[181]. Plusieurs groupes de chercheurs ont suggéré que l'alignement pourrait être la signature d'une nouvelle physique s'appliquant à grande échelle, ce que d'autres groupes rejettent en invoquant des erreurs systématiques dans les données[182],[183],[184]. À cause des effets locaux et de la variance cosmique (incertitude statistique sur les observations de l'Univers à de très grandes distances), les mesures à grande échelle ne seront jamais meilleures que les mesures à petite échelle angulaire[73],[83],[185]. Des analyses ultérieures montrent que les mesures dans la bande de fréquence micro-ondes sont sensibles à la pollution électromagnétique due au bremsstrahlung, au rayonnement synchrotron et à la poussière cosmique ; elles sont aussi entachées d'erreurs à cause des incertitudes expérimentales sur le monopôle et le dipôle électromagnétiques. Une analyse bayésienne complète du spectre de puissance, à partir des mesures de WMAP, étaie la prédiction du quadrupôle par le modèle ΛCDM, alors que l'octupôle observé n'est pas jugé significatif[186]. Publiées en 2013, des observations de l'équipe de l'télescope spatial Planck, qui emportait des instruments beaucoup plus sensibles que WMAP, rapporte la même anomalie en ce qui concerne l'alignement. Les erreurs instrumentales (mais pas la contamination d'avant-plan) sont donc à exclure[187]. Le responsable scientifique de l'équipe WMAP, Charles Bennett, a suggéré une coïncidence : « Je pense qu'il y a un effet psychologique ; les gens veulent trouver des choses insolites »[trad 5],[188].

Observations d'amateurs

Douglas Scott, un astronome de l'université de la Colombie-Britannique, émet en 2001 l'idée qu'en l'absence d'un canal hertzien, les téléviseurs analogiques affichent un bruit monochrome intense, « la neige », composée dans un faible pourcentage[11] — de l'ordre du pour cent[98] — de signaux issus du fond diffus. L'appareil capte des photons de la surface de dernière diffusion et en établit une représentation visuelle[189]. Même si elle est largement reprise, cette idée suscite des interrogations et en 2016, Leonard Burtscher, alors chercheur à l'Institut Max-Planck de physique extraterrestre, évalue la possibilité de sa mise en œuvre. Il détermine que le bruit du fond diffus reçu par un téléviseur ordinaire est environ 200 000 fois moins puissant que son bruit propre, ce qui rend l'éventualité de le « voir » très hypothétique[190].

Mais même s'il est très faible, des amateurs avec des moyens limités se sont lancés dans la mesure de la puissance du fond diffus cosmologique. Ainsi en 2008, deux astronomes amateurs construisent un radiomètre sur la base d'une antenne de réception de télévision par satellite d'un mètre de diamètre protégée des rayonnements parasites par un écran en papier d'aluminium. Leur système est calibré à l'eau, ce qui ne les empêche pas de trouver une température du fond diffus comprise entre 3,6 et 4,5 K[191].

Avec le même objectif et en utilisant uniquement des éléments d'occasion peu coûteux, Jack Gelfand présente en 2017 un radiomètre équipé d'une antenne cornet d'une longueur de 23 cm et d'un LNB normalement destiné à la réception de la télévision par satellite. Sa calibration à l'azote liquide lui permet d'évaluer la température du fond diffus à 3,9 K[192].

Fond diffus cosmologique et Big Bang

modifier
« Ce que la découverte finale, en 1965, du fond de rayonnement à 3 degrés Kelvin [sic] accomplit de plus important fut de nous forcer à prendre au sérieux l'idée qu'il y eut effectivement un commencement de l'univers[193]. »
— Steven Weinberg, 1978

À la fin des années 1940, Alpher et Herman concluent que si Big Bang il y avait, l'expansion de l'Univers aurait dilué l'énergie du plasma, abaissant la température du rayonnement issu du plasma pour l'amener dans la région des micro-ondes du spectre électromagnétique, ce qui correspond à une température d'environ 5 K. Leur estimation est légèrement erronée, mais ils ont posé les bonnes hypothèses. Même s'ils prédisent l'existence du CMB, c'est seulement 15 ans plus tard que Penzias et Wilson découvrent fortuitement le fond cosmique de micro-ondes[194].

Grâce à la précision de ses instruments de mesure, la mission d'observation Planck a permis d'éliminer quelques modèles cosmologiques. L'Univers serait constitué d'à peine 5 % de matière ordinaire (la plus courante sur Terre), d'environ 68 % d'énergie sombre et d'environ 27 % de matière noire[195].

La découverte du CMB dans les années 1960 provoque une perte d'intérêt pour tous les modèles alternatifs, telle la théorie de l'état stationnaire[196],[197] (ou théorie de la création continue[198]). Le CMB[199] et la loi de Hubble-Lemaître (traduite comme « fuite des galaxies éloignées »[200]) constituent en effet deux preuves de poids en faveur de la théorie du Big Bang, qui est, grâce aux observations du CMB, le meilleur modèle standard cosmologique en 2005[201],[h].

Le CMB fournit un instantané de l'Univers au moment où, selon le modèle standard cosmologique, sa température a suffisamment décru pour que les électrons et les protons forment des atomes d'hydrogène, rendant l'Univers presque transparent au rayonnement, parce que les photons ne sont plus alors diffusés par les électrons libres. Lorsque le CMB apparaît 380 000 ans après le Big Bang[202] — époque appelée « temps de la dernière diffusion »[trad 6], période de la recombinaison ou période de découplage —, la température de l'Univers atteint environ 3 000 K[203]. Elle correspond à une énergie d'environ 0,26 eV[204],[205], ce qui est nettement plus faible que l'énergie d'ionisation de l'hydrogène : 13,6 eV[206] (les photons ne peuvent donc pas modifier sensiblement l'état énergétique des atomes d'hydrogène).

Selon le modèle du Big Bang, l'inflation cosmique prédit qu'environ 10−37 s après sa naissance[207], l'Univers croît exponentiellement, période qui élimine presque toutes les irrégularités. Les fluctuations quantiques de l'inflaton (hypothétique source de l'inflation exponentielle[208],[209],[210]) sont la cause des irrégularités restantes[211]. Avant la création des étoiles et des planètes, l'Univers est plus petit, beaucoup plus chaud et rempli d'une lueur uniforme, issue d'un plasma blanc, siège de réactions entre les photons, les électrons et les baryons. Pendant l'expansion de l'Univers, le refroidissement adiabatique réduit la densité énergétique du plasma jusqu'à une température favorable au regroupement des électrons et des protons, époque de formation de l'hydrogène atomique. Cette recombinaison commence lorsque la température atteint 4 000 K[212],[213] ou proche de 3 000 K[214],[215] ; l'Univers est alors âgé d'environ 379 000 ans[5]. Les photons ne réagissant pas avec ces atomes électriquement neutres, ils commencent à se propager dans l'Univers sans diffuser, début du découplage du rayonnement (moment où la matière et les photons cessent d'être en équilibre thermique[216])[217].

La température de couleur de l'ensemble des photons découplés a décru sans arrêt depuis cette époque. Il y a 12,8 milliards d'années (z = 6,34) — donc 900 millions d'années après le Big Bang, elle était de 23,3 ± 6,9 K (1σ)[218],[219], en accord avec le modèle ΛCDM (qui prédit 20,0 K)[i]. Aujourd'hui, elle est de 2,726 0 ± 0,001 3 K[220] et même[pas clair] de 2,725 48 ± 0,000 57 K. Elle continue de diminuer (de 2 nK par année), puisque la taille de l'Univers continue d'augmenter. Elle équivaut donc à celle d'un corps noir à très basse température : 2,726 K. Selon le paradigme du Big Bang, le rayonnement actuel provient de la surface de dernière diffusion. Cette origine serait constituée par l'ensemble des endroits à la surface du plasma primitif où le découplage s'est manifesté[221], et serait donc le lieu d'où proviennent les photons du CMB détectés aujourd'hui par les instruments d'observation.

Depuis la recombinaison, la température du CMB a été divisée par environ 1 100[83], à cause de l'expansion de l'Univers. Pendant celle-ci, les photons du CMB ont été décalés vers le rouge, ce qui a diminué leur niveau d'énergie. Leur température moyenne est inversement proportionnelle au facteur d'échelle, a, paramètre qui décrit l'expansion temporelle de l'Univers[222]. Si l'Univers poursuit son expansion, le fond diffus cosmologique va continuer à se décaler vers le rouge jusqu'au point de ne plus être détectable[223], car son spectre sera surpassé à la fois par les spectres d'émission des étoiles et par d'autres rayonnements d'arrière-plan qui devraient être observés dans un très lointain futur[224].

Les infimes écarts de température du CMB indiquent que « l'espace cosmique est plat » ou encore que « l'espace cosmique a une courbure nulle ! (Presque nulle, aux incertitudes observationnelles près) »[225],[j]. En 2008, des chercheurs, s'appuyant sur l'étude des harmoniques sphériques du CMB, avancent que l'Univers ne serait pas euclidien et infini, il serait plutôt un espace dodécaédrique de Poincaré[226]. Selon le cosmologiste Joseph Silk, le CMB constitue un « référentiel cosmique » qui peut servir à valider le principe de Mach[227]. En 2019, trois astrophysiciens, analysant autrement les données sur le CMB transmises par le télescope spatial Planck, avancent que l'Univers serait courbe ; leur conclusion est toutefois accueillie avec réserve ou rejetée parce que ces données présentent des fluctuations statistiques. Les trois chercheurs observent également des variations de couleur statistiquement significatives « lorsqu'ils comparent de petites régions du ciel et quand ils comparent de grandes régions »[trad 7] selon un modèle d'Univers plat. S'il était courbe, ces variations n'apparaîtraient pas. Toutefois, leur modèle d'Univers courbe ne permet pas d'éliminer le problème de la valeur de la constante de Hubble[k],[229],[230].

Dans la culture

modifier

L'artiste canadien Nicolas Baier a produit la Pouponnière, un photomontage qui montre une version du fond diffus cosmologique[231],[232].

Notes et références

modifier

Citations originales

modifier
  1. ↑ (en) « By the formula E = σT4 the effective temperature corresponding to this density is 3º.18 absolute »
  2. ↑ (en) « It can be calculated that the 'rotational temperature' of interstellar space is 2 K. »
  3. ↑ (en) « the absolute effective temperature of the radioemission background ... is 4±3 K »
  4. ↑ (en) « delineate cosmic variance about the model »
  5. ↑ (en) « I do think there is a bit of a psychological effect; people want to find unusual things. »
  6. ↑ (en) « time of last scattering »
  7. ↑ (en) « when they compare small regions of the sky and when they compare large regions »

Notes

modifier
  1. ↑ 379 000 ans selon la collaboration WMAP en 2007[5].
  2. ↑ Pour le distinguer des autres fonds diffus, tels que les fonds diffus infrarouge, radio, de rayons X, gravitationnel et de neutrinos[11].
  3. ↑ En électronique, la température de bruit est proportionnelle à la fréquence du bruit électronique.
  4. ↑ Cette illustration provient de la NASA[68]. Dans les trois cartes à la droite, la contribution de la Voie Lactée, qui se trouve au centre des cartes, n’a pas été retirée parce que des cartes sans contribution de la Voie lactée n'ont pas été publiées sous une licence compatible avec la licence de Wikipédia.
  5. ↑ Silk 1997, p. 175, écrit « [...] on peut quasiment considérer les fluctuations comme des ondes de pression (ou des ondes sonores) ».
  6. ↑ À titre comparatif, la mission WMAP a rapporté 4,6 % de matière ordinaire, 22,7 % de matière noire et 72,8 % d'énergie noire (Drissen 2011, p. 245).
  7. ↑ La Terre se déplace à une vitesse d'environ 600 km/s. La distribution de température du ciel obéit à la loi de l'effet Doppler, qui s'exprime approximativement pour cette vitesse par :
    où est l'angle entre la direction d'observation et celle de la vitesse de la Terre. La composante en (la Terre se dirige vers la surface de dernière diffusion) correspond au dipôle, alors que la composante en (la vitesse radiale de la Terre par rapport à la surface de dernière diffusion) correspond au quadrupôle (Lachièze-Rey et Gunzig 1995, p. 193-194).
  8. ↑ Le physicien Steven Weinberg indique dès 1978 que c'est déjà le meilleur modèle (Weinberg 1978, p. 14).
  9. ↑ Le modèle ΛCDM prédit avec 2,725 48 ± 0,000 57 K[219].
  10. ↑ En effet, le paramètre de courbure cosmologique 1 − Ω = Ωk = −k c2 a-2 H-2, vaut 0,000 7 ± 0,001 9, valeurs arrondies à 0,001 ± 0,002, selon les données 2018 de la collaboration Planck, sachant que la courbure est positive si k = +1, Ωk < 0, Ω > 1 (pour un univers fermé à géométrie elliptique, ou espace ou géométrie elliptique de Cayley-Klein), négative si k = −1, Ωk > 0, Ω < 1 (pour un univers ouvert à géométrie hyperbolique, ou espace ou géométrie hyperbolique de Boliay-Lobatchevski), et nulle si k = 0, Ωk = 0, Ω = 1.
  11. ↑ La constante de Hubble calculée selon les observations du Big Bang diffère de la constante de Hubble calculée à partir d'observations de supernovas[228].

Références

modifier
  1. ↑ Sarah Sermondadaz, « Question de la semaine : Pourquoi le fond cosmologique est représenté comme une carte ovale ? », Science & Avenir, .
  2. ↑ Drissen 2011, p. 245.
  3. ↑ Clegg 2017, p. 133.
  4. ↑ Lachièze-Rey et Gunzig 1995, p. 31.
  5. ↑ a et b (en) B. Abbott, « Microwave (WMAP) All-Sky Survey », Hayden Planetarium, (consulté le ).
  6. ↑ Tegmark 2018, p. 88.
  7. ↑ a et b Tegmark 2018, p. 84.
  8. ↑ Weinberg 1978, p. 65.
  9. ↑ Lachièze-Rey et Gunzig 1995, p. 3.
  10. ↑ (en) « Cosmic Microwave Background [1 record] », Termium, .
  11. ↑ a et b (en) Douglas Scott, « Frequently Asked Questions », Astronomy and Astrophysics at the University of British Columbia, .
  12. ↑ « (Demande de traduction) », Google, .
  13. ↑ (en) « (Demande d traduction) », DeepL, (dans la boîte de dialogue de gauche, écrire « Cosmic Microwave Background »).
  14. ↑ (en) « (Recherche) « CMB "Cosmic Microwave Background" » », Google Scholar, .
  15. ↑ C.-É. Guillaume, « La température de l'espace », La Nature, no 1214,‎
    Cité dans A. K. T. Assis et M. C. D. Neves, « History of the 2.7 K Temperature Prior to Penzias and Wilson », Apeiron, vol. 2, no 3,‎ , p. 80 (lire en ligne [PDF]).
  16. ↑ (en) « The Internal Constitution of the Stars », Science, vol. 66, no 1699,‎ , p. 82 (DOI 10.1126/science.66.1699.81-a)
    Cité dans A. K. T. Assis et M. C. D. Neves, « History of the 2.7 K Temperature Prior to Penzias and Wilson », Apeiron, vol. 2, no 3,‎ , p. 80 (lire en ligne [PDF]).
  17. ↑ Lachièze-Rey et Gunzig 1995, p. 86-87.
  18. ↑ (en) H. Kragh, Cosmology and Controversy: The Historical Development of Two Theories of the Universe, Princeton University Press, (ISBN 0-691-00546-X, lire en ligne), p. 135.
  19. ↑ (en) Robert H. Dicke, Robert Beringer, Robert L. Kyhl et A. B. Vane, « Atmospheric Absorption Measurements with a Microwave Radiometer », Physical Review, vol. 70, nos 5-6,‎ , p. 340–348 (DOI 10.1103/PhysRev.70.340, Bibcode 1946PhRv...70..340D).
  20. ↑ Hladik 2017, p. 144.
  21. ↑ Lachièze-Rey et Gunzig 1995, p. 25-26.
  22. ↑ Weinberg 1978, p. 141.
  23. ↑ Roman Ikonicoff, « Une étude confirme que l'Univers n'a pas de direction privilégiée », Science & Vie,‎ (lire en ligne).
  24. ↑ Hladik 2017, p. 135.
  25. ↑ Hladik 2017, p. 133-134.
  26. ↑ Dominique Lambert, « L'hypothèse de l'atome primitif », Pour la science - Les Génies de la science, no 30,‎ février - avril 2007 (lire en ligne).
  27. ↑ a et b Lachièze-Rey et Gunzig 1995, p. 1.
  28. ↑ (en) G. Gamow, « The Origin of Elements and the Separation of Galaxies », Physical Review, vol. 74, no 4,‎ , p. 505–506 (DOI 10.1103/PhysRev.74.505.2, Bibcode 1948PhRv...74..505G).
  29. ↑ (en) G. Gamow, « The Evolution of the Universe », Nature, vol. 162, no 4122,‎ , p. 680–682 (PMID 18893719, DOI 10.1038/162680a0, Bibcode 1948Natur.162..680G).
  30. ↑ (en) R. A. Alpher et R. C. Herman, « On the Relative Abundance of the Elements », Physical Review, vol. 74, no 12,‎ , p. 1737–1742 (DOI 10.1103/PhysRev.74.1737, Bibcode 1948PhRv...74.1737A).
  31. ↑ Weinberg 1978, p. 146-147.
  32. ↑ (en) A. K. T. Assis et M. C. D. Neves, « History of the 2.7 K Temperature Prior to Penzias and Wilson », Apeiron, vol. 2, no 3,‎ , p. 79-87 (lire en ligne [PDF]).
  33. ↑ (en) E. L. Wright, « Eddington's Temperature of Space », UCLA, (consulté le ).
  34. ↑ (en) A. McKellar, « Molecular Lines from the Lowest States of Diatomic Molecules Composed of Atoms Probably Present in Interstellar Space », Publications of the Dominion Astrophysical Observatory, Vancouver, B.C., Canada, vol. 7, no 6,‎ , p. 251–272 (Bibcode 1941PDAO....7..251P).
  35. ↑ Reeves 1994, p. 131-132.
  36. ↑ (en) H. Kragh, Cosmology and Controversy: The Historical Development of Two Theories of the Universe, Princeton University Press, (lire en ligne), p. 343.
  37. ↑ Reeves 1994, p. 132.
  38. ↑ (ru) T. A. Shmaonov, « Commentary », Pribory i Tekhnika Experimenta , vol. 1,‎ , p. 83 (DOI 10.1016/S0890-5096(06)60772-3).
  39. ↑ (en) P. D. Naselsky, D.I. Novikov et I. D. Novikov, The Physics of the Cosmic Microwave Background, (ISBN 0-521-85550-0, lire en ligne).
  40. ↑ (en) A. A. Penzias, « The Origin of Elements » [PDF], Nobel lecture, Fondation Nobel, (consulté le ).
  41. ↑ (en) R. H. Dicke, « The Measurement of Thermal Radiation at Microwave Frequencies », Review of Scientific Instruments, vol. 17, no 7,‎ , p. 268–275 (PMID 20991753, DOI 10.1063/1.1770483, Bibcode 1946RScI...17..268D).
  42. ↑ a et b (en) « for their discovery of cosmic microwave background radiation » in Personnel de rédaction, « The Nobel Prize in Physics 1978 », Fondation Nobel, 2010. Consulté le 20 juin 2010.
  43. ↑ (en) R. H. Dicke, « Cosmic Black-Body Radiation », The Astrophysical Journal, vol. 142,‎ , p. 414–419 (DOI 10.1086/148306, Bibcode 1965ApJ...142..414D).
  44. ↑ (en) P. J. E Peebles, Principles of Physical Cosmology, Princeton University Press, , 139–148 p. (ISBN 0-691-01933-9).
  45. ↑ (en) A. A. Penzias et R. W. Wilson, « A Measurement of Excess Antenna Temperature at 4080 Mc/s », The Astrophysical Journal , vol. 142, no 1,‎ , p. 419–421 (DOI 10.1086/148307, Bibcode 1965ApJ...142..419P).
  46. ↑ (en) Smoot Group , « The Cosmic Microwave Background Radiation », Lawrence Berkeley Lab, (consulté le ).
  47. ↑ Reeves 1988, p. 56-57.
  48. ↑ a b et c Heidmann 1968, p. 123.
  49. ↑ (en) Douglas Scott, « The Cosmic Microwave Background », Astronomy and Astrophysics at the University of British Columbia , .
    « [...] any attempt to interpret the origin of the CMB as due to present astrophysical phenomena (i.e. stars, dust, radio galaxies, etc.) is no longer credible. ».
  50. ↑ (en) J. V. Narlikar et N. C. Wickramasinghe, « Microwave Background in a Steady State Universe », Nature, vol. 216, no 5110,‎ , p. 43–44 (DOI 10.1038/216043a0, Bibcode 1967Natur.216...43N).
  51. ↑ (en) P. J. E. Peebles, « The case for the relativistic hot big bang cosmology », Nature, vol. 352, no 6338,‎ , p. 769–776 (DOI 10.1038/352769a0, Bibcode 1991Natur.352..769P).
  52. ↑ (en) E. R. Harrison, « Fluctuations at the threshold of classical cosmology », Physical Review D, vol. 1, no 10,‎ , p. 2726–2730 (DOI 10.1103/PhysRevD.1.2726, Bibcode 1970PhRvD...1.2726H).
  53. ↑ (en) P. J. E. Peebles et J. T. Yu, « Primeval Adiabatic Perturbation in an Expanding Universe », The Astrophysical Journal, vol. 162,‎ , p. 815–836 (DOI 10.1086/150713, Bibcode 1970ApJ...162..815P).
  54. ↑ (en) Y. B. Zeldovich, « A hypothesis, unifying the structure and the entropy of the Universe », Monthly Notices of the Royal Astronomical Society, vol. 160, nos 7–8,‎ , p. 1P–4P (DOI 10.1016/S0026-0576(07)80178-4).
  55. ↑ (en) A. G. Doroshkevich, Y. B. Zel'Dovich et R. A. Syunyaev « Fluctuations of the microwave background radiation in the adiabatic and entropic theories of galaxy formation » (Bibcode 1978IAUS...79..393S)
    — IAU, The large scale structure of the universe (Tallinn, 12–16 septembre 1977)
    — « (ibid.) », dans M. S. Longair and J. Einasto (éds.), The large scale structure of the universe; Proceedings of the Symposium, Dordrecht, D. Reidel Publishing Co., , p. 393–404
    Même si c'est le premier article à présenter une étude détaillée de l'empreinte observable de la densité des inhomogénéités en tant qu'anisotropies du CMB, quelques travaux préliminaires avaient déjà été faits par Peebles et Yu 1970.
    .
  56. ↑ (en) G. F. Smooth, « Structure in the COBE differential microwave radiometer first-year maps », The Astrophysical Journal Letters, vol. 396, no 1,‎ , L1–L5 (DOI 10.1086/186504, Bibcode 1992ApJ...396L...1S).
  57. ↑ (en) C.L. Bennett, « Four-Year COBE DMR Cosmic Microwave Background Observations: Maps and Basic Results », The Astrophysical Journal Letters, vol. 464,‎ , L1–L4 (DOI 10.1086/310075, Bibcode 1996ApJ...464L...1B, arXiv astro-ph/9601067).
  58. ↑ (en) « for their discovery of the blackbody form and anisotropy of the cosmic microwave background radiation » in Personnel de rédaction, « The Nobel Prize in Physics 2006 », Fondation Nobel, 2010. Consulté le 1er juillet 2010.
  59. ↑ Reeves 1988, p. 308.
  60. ↑ Lachièze-Rey et Gunzig 1995, p. 91.
  61. ↑ Lachièze-Rey et Gunzig 1995, p. 91-92.
  62. ↑ (en) « Positions and Sizes of Cosmic Objects », Space Book - Las Cumbres Observatory, .
  63. ↑ Lachièze-Rey et Gunzig 1995, p. 159, 184 et 169.
  64. ↑ Par exemple, Lachièze-Rey et Gunzig 1995, p. 149-151, 169-181 et 185-190 discutent de dizaines d'expériences menées dans ce but.
  65. ↑ Lachièze-Rey et Gunzig 1995, p. 145-146.
  66. ↑ Lachièze-Rey et Gunzig 1995, p. 146.
  67. ↑ (en) « NASA and COBE Scientists Win Top Cosmology Prize », NASA, .
  68. ↑ (en) « A Brief History of Background Radiation », NASA, .
  69. ↑ (en) C. Grupen, Astroparticle Physics, Springer, , 240–241 p. (ISBN 3-540-25312-2).
  70. ↑ (en) A. D. Miller, « A Measurement of the Angular Power Spectrum of the Microwave Background Made from the High Chilean Andes », The Astrophysical Journal, vol. 521, no 2,‎ , L79–L82 (DOI 10.1086/312197, Bibcode 1999ApJ...521L..79T, arXiv astro-ph/9905100).
  71. ↑ (en) A. Melchiorri, « A Measurement of Ω from the North American Test Flight of Boomerang », The Astrophysical Journal Letters, vol. 536, no 2,‎ , L63–L66 (DOI 10.1086/312744, Bibcode 2000ApJ...536L..63M, arXiv astro-ph/9911445).
  72. ↑ (en) S. Hanany, « MAXIMA-1: A Measurement of the Cosmic Microwave Background Anisotropy on Angular Scales of 10'–5° », The Astrophysical Journal, vol. 545, no 1,‎ , L5–L9 (DOI 10.1086/317322, Bibcode 2000ApJ...545L...5H, arXiv astro-ph/0005123).
  73. ↑ a et b (en) G. Hinshaw, (WMAP collaboration), C. L. Bennett, R. Bean, O. Doré, M. R. Greason, M. Halpern, R. S. Hill, N. Jarosik, A. Kogut, E. Komatsu, M. Limon, N. Odegard, S. S. Meyer, L. Page, H. V. Peiris, D. N. Spergel, G. S. Tucker, L. Verde, J. L. Weiland, E. Wollack et E. L. Wright, « Three-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: temperature analysis », Astrophysical Journal Supplement Series, vol. 170, no 2,‎ , p. 288–334 (DOI 10.1086/513698, Bibcode 2007ApJS..170..288H, arXiv astro-ph/0603451).
  74. ↑ Clegg 2017, p. 132.
  75. ↑ (en) « B2K: Measurements of CMB Polarization with BOOMERanG », Experimental Cosmology Group G31 , (consulté le ).
  76. ↑ a et b (en) E.M. Leitch, « Measurement of polarization with the Degree Angular Scale Interferometer », Nature, vol. 420, no 6917,‎ , p. 763–771 (PMID 12490940, DOI 10.1038/nature01271, Bibcode 2002Natur.420..763L, arXiv astro-ph/0209476).
  77. ↑ (en) The Planck Collaboration, « The Scientific Programme of Planck », ..
  78. ↑ (en) QUaD collaboration, « First season QUaD CMB temperature and polarization power spectra », The Astrophysical Journal , vol. 674, no 2008,‎ , p. 22–28 (DOI 10.1086/524922, Bibcode 2008ApJ...674...22A, arXiv 0705.2359).
  79. ↑ (en) J. E. Carlstrom, « The 10 Meter South Pole Telescope », Publications of the Astronomical Society of the Pacific, vol. 123, no 903,‎ , p. 568–581 (DOI 10.1086/659879, Bibcode 2011PASP..123..568C, arXiv 0907.4445).
  80. ↑ (en) A. Fowler et ACT Collaboration, « The Atacama Cosmology Telescope: A Measurement of the 600 < >>>ℓ < 8000 Cosmic Microwave Background Power Spectrum at 148 GHz », The Astrophysical Journal, vol. 722, no 2,‎ , p. 1148–1161 (DOI 10.1088/0004-637X/722/2/1148, Bibcode 2010ApJ...722.1148F, arXiv 1001.2934).
  81. ↑ (en) « QUIET (Q/U Imaging ExperimenT) », QUIET collaboration, (consulté le ).
  82. ↑ (en) « The WMAP Achievement: A Detailed Picture of the Early Universe », NASA (consulté le ).
  83. ↑ a b et c (en) C. L. Bennett, (WMAP collaboration), G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer, L. Page, D. N. Spergel, G. S. Tucker, E. Wollack, E. L. Wright, C. Barnes, M. R. Greason, R. S. Hill, E. Komatsu, M. R. Nolta, N. Odegard, H. V. Peiris, L. Verde et J. L. Weiland, « First-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: preliminary maps and basic results », Astrophysical Journal Supplement Series, vol. 148,‎ , p. 1–27 (DOI 10.1086/377253, Bibcode 2003ApJS..148....1B, arXiv astro-ph/0302207). Cet article fait une mise en garde, indiquant que les calculs statistiques sont complexes et ne peuvent servir dans la plupart des analyses du CMB.
  84. ↑ Reeves 1994, p. 119.
  85. ↑ (en) « History of Planck », sur Missions scientifiques de l'ESA, Agence spatiale européenne (consulté le ).
  86. ↑ (en) Takashi Mimura, « The Early History of the High Electron Mobility Transistor (HEMT) », IEEE Transactions on Microwave Theory and Techniques , vol. 50, no 3,‎ .
  87. ↑ Lachièze-Rey et Gunzig 1995, p. 140-141.
  88. ↑ (en) J.-M. Lamarre, J.-L. Puget, P. A. R. Ade, F. Bouchet, G. Guyot, A. E. Lange, F. Pajot, A. Arondel, K. Benabed, J.-L. Beney, A. Benoît, J.-Ph. Bernard, R. Bhatia, Y. Blanc, J. J. Bock, E. Bréelle, T. W. Bradshaw, P. Camus, A. Catalano, J. Charra, M. Charra, S. E. Church, F. Couchot, A. Coulais, B. P. Crill, M. R. Crook, K. Dassas, P. de Bernardis, J. Delabrouille, P. de Marcillac, J.-M. Delouis, F.-X. Désert, C. Dumesnil, X. Dupac, G. Efstathiou, P. Eng, C. Evesque, J.-J. Fourmond, K. Ganga, M. Giard, R. Gispert, L. Guglielmi, J. Haissinski, S. Henrot-Versillé, E. Hivon, W. A. Holmes, W. C. Jones, T. C. Koch, H. Lagardère, P. Lami, J. Landé, B. Leriche, C. Leroy, Y. Longval, J. F. Macías-Pérez, T. Maciaszek, B. Maffei, B. Mansoux, C. Marty, S. Masi, C. Mercier, M.-A. Miville-Deschênes, A. Moneti, L. Montier, J. A. Murphy, J. Narbonne, M. Nexon, C. G. Paine, J. Pahn, O. Perdereau, F. Piacentini, M. Piat, S. Plaszczynski, E. Pointecouteau, R. Pons, N. Ponthieu, S. Prunet, D. Rambaud, G. Recouvreur, C. Renault, I. Ristorcelli, C. Rosset, D. Santos, G. Savini, G. Serra, P. Stassi, R. V. Sudiwala, J.-F. Sygnet, J. A. Tauber, J.-P. Torre, M. Tristram, L. Vibert, A. Woodcraft, V. Yurchenko et D. Yvon, « Planck pre-launch status: The HFI instrument, from specification to actual performance », Astronomy and Astrophysics , vol. 520,‎ , p. 1-20 (ISSN 0004-6361, DOI 10.1051/0004-6361/200912975, lire en ligne [PDF]).
  89. ↑ (en) « Arcminute Cosmology Bolometer Array Receiver - Instrument Description », Holzapfel Group, .
  90. ↑ (en) C. L. Reichardt, P. A. R. Ade, J. J. Bock, J. R. Bond, J. A. Brevik, C. R. Contaldi, M. D. Daub, J. T. Dempsey, J. H. Goldstein, W. L. Holzapfel, C. L. Kuo, A. E. Lange, M. Lueker, M. Newcomb, J. B. Peterson, J. Ruhl, M. C. Runyan et Z. Staniszewski, « High-Resolution Cmb Power Spectrum From the Complete Acbar Data Set », The Astrophysical Journal , vol. 694, no 2,‎ , p. 1200–1219 (ISSN 0004-637X, DOI 10.1088/0004-637X/694/2/1200, Bibcode 2009ApJ...694.1200R, arXiv 0801.1491).
  91. ↑ (en) A. Benoit, « Archeops: A High Resolution, Large Sky Coverage Balloon Experiment for Mapping CMB Anisotropies », Astropart. Phys., vol. 17,‎ , p. 101–124 (DOI 10.1016/S0927-6505(01)00141-4, Bibcode 2002APh....17..101B, arXiv astro-ph/0106152).
  92. ↑
  93. ↑ (en) (Rédaction), « Mapping the Early Universe », The New York Times , (consulté le ).
  94. ↑ (en) Whitney Clavin et J.D. Harrington, « Planck Mission Brings Universe Into Sharp Focus », NASA, (consulté le ).
  95. ↑ (en) P. A. R. Ade, N. Aghanim, M. Arnaud, M. Ashdown, J. Aumont, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, N. Bartolo, E. Battaner, R. Battye, K. Benabed, A. Benoît, A. Benoit-Lévy, J.-P. Bernard, M. Bersanelli, P. Bielewicz, J. J. Bock, A. Bonaldi, L. Bonavera, J. R. Bond, J. Borrill, F. R. Bouchet, F. Boulanger, M. Bucher, C. Burigana, R. C. Butler, E. Calabrese, J.-F. Cardoso, A. Catalano, A. Challinor, A. Chamballu, R.-R. Chary, H. C. Chiang, J. Chluba, P. R. Christensen, S. Church, D. L. Clements, S. Colombi, L. P. L. Colombo, C. Combet, A. Coulais, B. P. Crill, A. Curto, F. Cuttaia, L. Danese, R. D. Davies, R. J. Davis, P. de Bernardis, A. de Rosa, G. de Zotti, J. Delabrouille, F.-X. Désert, E. Di Valentino, C. Dickinson, J. M. Diego, K. Dolag, H. Dole, S. Donzelli, O. Doré, M. Douspis, A. Ducout, J. Dunkley, X. Dupac, G. Efstathiou, F. Elsner, T. A. Enßlin, H. K. Eriksen, M. Farhang, J. Fergusson, F. Finelli, O. Forni, M. Frailis, A. A. Fraisse, E. Franceschi, A. Frejsel, S. Galeotta, S. Galli, K. Ganga, C. Gauthier, M. Gerbino, T. Ghosh, M. Giard, Y. Giraud-Héraud, E. Giusarma, E. Gjerløw, J. González-Nuevo, K. M. Górski, S. Gratton, A. Gregorio, A. Gruppuso, J. E. Gudmundsson, J. Hamann, F. K. Hansen, D. Hanson, D. L. Harrison, G. Helou, S. Henrot-Versillé, C. Hernández-Monteagudo, D. Herranz, S. R. Hildebrandt, E. Hivon, M. Hobson, W. A. Holmes, A. Hornstrup, W. Hovest, Z. Huang, K. M. Huffenberger, G. Hurier, A. H. Jaffe, T. R. Jaffe, W. C. Jones, M. Juvela, E. Keihänen, R. Keskitalo, T. S. Kisner, R. Kneissl, J. Knoche, L. Knox, M. Kunz, H. Kurki-Suonio, G. Lagache, A. Lähteenmäki, J.-M. Lamarre, A. Lasenby, M. Lattanzi, C. R. Lawrence, J. P. Leahy, R. Leonardi, J. Lesgourgues, F. Levrier, A. Lewis, M. Liguori, P. B. Lilje, M. Linden-Vørnle, M. López-Caniego, P. M. Lubin, J. F. Macías-Pérez, G. Maggio, D. Maino, N. Mandolesi, A. Mangilli, A. Marchini, M. Maris, P. G. Martin, M. Martinelli, E. Martínez-González, S. Masi, S. Matarrese, P. McGehee, P. R. Meinhold, A. Melchiorri, J.-B. Melin, L. Mendes, A. Mennella, M. Migliaccio, M. Millea, S. Mitra, M.-A. Miville-Deschênes, A. Moneti, L. Montier, G. Morgante, D. Mortlock, A. Moss, D. Munshi, J. A. Murphy, P. Naselsky, F. Nati, P. Natoli, C. B. Netterfield, H. U. Nørgaard-Nielsen, F. Noviello, D. Novikov, I. Novikov, C. A. Oxborrow, F. Paci, L. Pagano, F. Pajot, R. Paladini, D. Paoletti, B. Partridge, F. Pasian, G. Patanchon, T. J. Pearson, O. Perdereau, L. Perotto, F. Perrotta, V. Pettorino, F. Piacentini, M. Piat, E. Pierpaoli, D. Pietrobon, S. Plaszczynski, E. Pointecouteau, G. Polenta, L. Popa, G. W. Pratt, G. Prézeau, S. Prunet, J.-L. Puget, J. P. Rachen, W. T. Reach, R. Rebolo, M. Reinecke, M. Remazeilles, C. Renault, A. Renzi, I. Ristorcelli, G. Rocha, C. Rosset, M. Rossetti, G. Roudier, B. Rouillé d’Orfeuil, M. Rowan-Robinson, J. A. Rubiño-Martín, B. Rusholme, N. Said, V. Salvatelli, L. Salvati, M. Sandri, D. Santos, M. Savelainen, G. Savini, D. Scott, M. D. Seiffert, P. Serra, E. P. S. Shellard, L. D. Spencer, M. Spinelli, V. Stolyarov, R. Stompor, R. Sudiwala, R. Sunyaev, D. Sutton, A.-S. Suur-Uski, J.-F. Sygnet, J. A. Tauber, L. Terenzi, L. Toffolatti, M. Tomasi, M. Tristram, T. Trombetti, M. Tucci, J. Tuovinen, M. Türler, G. Umana, L. Valenziano, J. Valiviita, F. Van Tent, P. Vielva, F. Villa, L. A. Wade, B. D. Wandelt, I. K. Wehus, M. White, S. D. M. White, A. Wilkinson, D. Yvon, A. Zacchei et A. Zonca, « Planck 2015 results », Astronomy & Astrophysics, vol. 594,‎ , p. 32, Table 4 (ISSN 0004-6361, DOI 10.1051/0004-6361/201525830, Bibcode 2016A&A...594A..13P, arXiv 1502.01589) (paramètres H0 et Age/Gyr, dernière colonne).
  96. ↑ a b et c Nabila Aghanim et Hervé Dole, « Les résultats cosmologiques de la mission Planck », Reflets de la physique, no 64,‎ , p. 4–7 (ISSN 1953-793X et 2102-6777, DOI 10.1051/refdp/202064004, lire en ligne, consulté le ).
  97. ↑ (en) Davide Castelvecchi, « Big Bang telescope finale marks end of an era in cosmology », Nature, vol. 559,‎ , p. 455-456 (DOI 10.1038/d41586-018-05788-5, lire en ligne).
  98. ↑ a et b « Le rayonnement fossile du cosmos », CNRS, .
  99. ↑ a b et c (en) Martin White, « Anisotropies in the CMB », dans Proceedings of the Los Angeles Meeting, DPF 99, UCLA, (Bibcode 1999dpf..conf.....W, arXiv astro-ph/9903232), p. 1.
  100. ↑ Serway 1992, p. 686.
  101. ↑ Lachièze-Rey et Gunzig 1995, quatrième de couverture.
  102. ↑ Lachièze-Rey et Gunzig 1995, p. 4.
  103. ↑ Silk 1997, p. 85-86.
  104. ↑ Weinberg 1978, p. 83.
  105. ↑ (en) D. J. Fixsen, E. S. Cheng, J. M. Gales, J. C. Mather, R. A. Shafer et E. L. Wright, « The Cosmic Microwave Background Spectrum from the FullCOBEFIRAS Data Set », The Astrophysical Journal, vol. 473, no 2,‎ , p. 576–587 (ISSN 0004-637X, DOI 10.1086/178173).
  106. ↑ Reeves 1994, p. 134.
  107. ↑ (en) E.L. Wright, « Theoretical Overview of Cosmic Microwave Background Anisotropy », dans W. L. Freedman, Measuring and Modeling the Universe, Cambridge University Press, coll. « Carnegie Observatories Astrophysics Series », (ISBN 0-521-75576-X, Bibcode 2004mmu..symp..291W, arXiv astro-ph/0305591), p. 291.
  108. ↑ (en) M.P. Hobson, G. Efstathiou et A.N. Lasenby, General Relativity: An Introduction for Physicists, Cambridge University Press, (ISBN 0-521-82951-8), p. 388.
  109. ↑ (en) A. Unsöld et B. Bodo, The New Cosmos, An Introduction to Astronomy and Astrophysics, Springer-Verlag, , 5e éd. (ISBN 3-540-67877-8), p. 485.
  110. ↑ (en) Malcolm S. Longair, Confrontation of Cosmological Theories with Observational Data, Springer Science & Business Media, (présentation en ligne), p. 144.
  111. ↑ (en) Ruth Durrer, « Cosmology II: The thermal history of the Universe » [PDF], .
  112. ↑ Weinberg 1978, p. 91.
  113. ↑ Silk 1997, p. 61.
  114. ↑ (en) Daniela Saadeh, Stephen M. Feeney, Andrew Pontzen, Hiranya V. Peiris et Jason D. McEwen, « How Isotropic is the Universe? », Physical Review Letters, vol. 117, no 13,‎ (DOI 10.1103/PhysRevLett.117.131302, arXiv 1605.07178v2, lire en ligne [PDF]).
  115. ↑ Lachièze-Rey et Gunzig 1995, p. 92-94.
  116. ↑ Lachièze-Rey et Gunzig 1995, p. 85, 89 et 108.
  117. ↑ Weinberg 1978, p. 92.
  118. ↑ (en) Arthur Kosowsky, chap. 7 « Cosmic Microwave Background », dans S. Bonometto, V. Gorini et U. Moschella, Modern Cosmology, Institute of Physics Publishing (Taylor & Francis), , 1re éd. (ISBN 0-7503-0810-9), p. 227-228.
  119. ↑ (en) « WMAP Data Product Images », Goddard Space Flight Center, NASA, , consulter la section WMAP CMB Power Spectra.
  120. ↑ Le terme « variance cosmique » dénote l'incertitude statistique sur les observations de l'Univers à de très grandes distances. Cette incertitude provient de l'impossibilité pour les cosmologistes de contre-vérifier leurs résultats avec un autre échantillon, puisqu'il n'y a qu'une seule région qu'ils peuvent étudier, d'un seul Univers[119]
  121. ↑ Tegmark 2018, p. 122.
  122. ↑ Reeves et al. 2008, p. 50.
  123. ↑ (en) Wayne Hu, « Baryons and Inertia », Department of Astronomy and Astrophysics, University of Chicago, .
  124. ↑ (en) Wayne Hu, « Radiation Driving Force », Department of Astronomy and Astrophysics, University of Chicago, .
  125. ↑ Lachièze-Rey et Gunzig 1995, p. 43-44.
  126. ↑ (en) W. Hu et M. White, « Acoustic Signatures in the Cosmic Microwave Background », The Astrophysical Journal, vol. 471,‎ , p. 30–51 (DOI 10.1086/177951, Bibcode 1996ApJ...471...30H, arXiv astro-ph/9602019).
  127. ↑ (en) WMAP Collaboration, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw et N. Jarosik, « First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters », Astrophysical Journal Supplement Series, vol. 148, no 1,‎ , p. 175–194 (DOI 10.1086/377226, Bibcode 2003ApJS..148..175S, arXiv astro-ph/0302209).
  128. ↑ Lachièze-Rey et Gunzig 1995, p. 123.
  129. ↑ (en) David N. Spergel, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer, L. Page, G. S. Tucker, J. L. Weiland, E. Wollack et E. L. Wright, « First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters », The Astrophysical Journal Supplement Series, vol. 148, no 1,‎ , p. 175–194 (DOI 10.1086/377226, arXiv astro-ph/0302209).
  130. ↑ (en) David N. Spergel, R. Bean, O. Dore, M. R. Nolta, C. L. Bennett, J. Dunkley, G. Hinshaw, N. Jarosik, E. Komatsu, L. Page, H. V. Peiris, L. Verde, M. Halpern, R. S. Hill, A. Kogut, M. Limon, S. S. Meyer, N. Odegard, G. S. Tucker, J. L. Weiland, E. Wollack et E. L. Wright, « Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for Cosmology », The Astrophysical Journal Supplement Series, vol. 170, no 2,‎ , p. 377–408 (DOI 10.1086/513700, arXiv astro-ph/0603449).
  131. ↑ Lachièze-Rey et Gunzig 1995, p. 108-109.
  132. ↑ Lachièze-Rey et Gunzig 1995, p. 94.
  133. ↑ Lachièze-Rey et Gunzig 1995, Avant-propos.
  134. ↑ Luminet 2001, p. 353.
  135. ↑ Séguin et Villeneuve 2002, p. 382.
  136. ↑ Lachièze-Rey et Gunzig 1995, p. 148.
  137. ↑ Consulter par exemple : Roger Penrose (trad. Céline Laroche), À la découverte des lois de l'Univers : La prodigieuse histoire des mathématiques et de la physique, Paris, O. Jacob, , XXII + 1061 (ISBN 978-2-7381-1840-0, lire en ligne), p. 444.
  138. ↑ Serway 1992, p. 295 (figure 8.21).
  139. ↑ a et b (en) Marc Kamionkowski, Arthur Kosowsky et Albert Stebbins, « Statistics of cosmic microwave background polarization », Physical Review D, vol. 55, no 12,‎ , p. 7368–7371 (DOI 10.1103/PhysRevD.55.7368, arXiv astro-ph/9611125.pdf, lire en ligne [PDF]).
  140. ↑ Serway 1992, p. 295-296.
  141. ↑ (en) J. M. Kovac, E. M. Leitch, C. Pryke, J. E. Carlstrom, N. W. Halverson et W. L. Holzapfel, « Detection of polarization in the cosmic microwave background using DASI », Nature, vol. 420, no 6917,‎ , p. 772–787 (PMID 12490941, DOI 10.1038/nature01269, Bibcode 2002Natur.420..772K, arXiv astro-ph/0209478).
  142. ↑ (en) A. C. S. Readhead, « Polarization Observations with the Cosmic Background Imager », Science, vol. 306, no 5697,‎ , p. 836–844 (PMID 15472038, DOI 10.1126/science.1105598, Bibcode 2004Sci...306..836R, arXiv astro-ph/0409569).
  143. ↑ (en) P. de Bernardis, « A flat Universe from high-resolution maps of the cosmic microwave background radiation », Nature, vol. 404, no 6781,‎ , p. 955–959 (PMID 10801117, DOI 10.1038/35010035, Bibcode 2000Natur.404..955D, arXiv astro-ph/0004404).
  144. ↑ (en) L. Pogosian, « Observational constraints on cosmic string production during brane inflation », Physical Review D, vol. 68, no 2,‎ , p. 023506 (DOI 10.1103/PhysRevD.68.023506, Bibcode 2003PhRvD..68b3506P, arXiv hep-th/0304188).
  145. ↑ (en) A. Lewis et A. Challinor, « Weak gravitational lensing of the CMB », Physics Reports, vol. 429,‎ , p. 1-65 (DOI 10.1016/j.physrep.2006.03.002, Bibcode 2006PhR...429....1L, arXiv astro-ph/0601594).
  146. ↑ (en) D. Hanson, « Detection of B-mode polarization in the Cosmic Microwave Background with data from the South Pole Telescope », Physical Review Letters, vol. 111, no 14,‎ (DOI 10.1103/PhysRevLett.111.141301, Bibcode 2013PhRvL.111n1301H, arXiv 1307.5830, lire en ligne).
  147. ↑ a et b (en) Eugenie Samuel Reich, « Polarization detected in Big Bang's echo », Nature,‎ (lire en ligne).
  148. ↑ (en) U. Seljak, « Measuring Polarization in the Cosmic Microwave Background », Astrophysical Journal, vol. 482,‎ , p. 6–16 (DOI 10.1086/304123, Bibcode 1997ApJ...482....6S, arXiv astro-ph/9608131).
  149. ↑ (en) U. Seljak et M. Zaldarriaga, « Signature of Gravity Waves in the Polarization of the Microwave Background », Phys. Rev. Lett., vol. 78, no 11,‎ , p. 2054–2057 (DOI 10.1103/PhysRevLett.78.2054, Bibcode 1997PhRvL..78.2054S, arXiv astro-ph/9609169).
  150. ↑ (en) M. Kamionkowski, A. Kosowsky et A. Stebbins, « A Probe of Primordial Gravity Waves and Vorticity », Phys. Rev. Lett., vol. 78, no 11,‎ , p. 2058–2061 (DOI 10.1103/PhysRevLett.78.2058, Bibcode 1997PhRvL..78.2058K, arXiv astro-ph/9609132).
  151. ↑ (en) M. Zaldarriaga et U. Seljak, « Gravitational lensing effect on cosmic microwave background polarization », Physical Review D, vol. 58, no 2,‎ (DOI 10.1103/PhysRevD.58.023003, Bibcode 1998PhRvD..58b3003Z, arXiv astro-ph/9803150).
  152. ↑ (en) Ben P. Stein, « Scientists Report Evidence for Gravitational Waves in Early Universe », Inside Science,‎ (lire en ligne, consulté le ).
  153. ↑ « Planck livre ses mesures de la polarisation du rayonnement de fond cosmologique », Insitut d'astrophysique de Paris, .
  154. ↑ (en) ESA Planck, « Planck Space Mission », (consulté le ).
  155. ↑ (en) NASA/Jet Propulsion Laboratory, « Long-sought pattern of ancient light detected », ScienceDaily,‎ (lire en ligne, consulté le ).
  156. ↑ (en) D. Hanson, « Detection of B-Mode Polarization in the Cosmic Microwave Background with Data from the South Pole Telescope », Physical Review Letters, vol. 111, no 14,‎ (DOI 10.1103/PhysRevLett.111.141301, Bibcode 2013PhRvL.111n1301H, arXiv 1307.5830).
  157. ↑ (en) The Polarbear Collaboration, « A Measurement of the Cosmic Microwave Background B-Mode Polarization Power Spectrum at Sub-Degree Scales with POLARBEAR », The Astrophysical Journal, vol. 794,‎ , p. 171 (DOI 10.1088/0004-637X/794/2/171, Bibcode 2014ApJ...794..171T, arXiv 1403.2369, lire en ligne [PDF], consulté le ).
  158. ↑ (en) « POLARBEAR project offers clues about origin of universe's cosmic growth spurt », Christian Science Monitor,‎ (lire en ligne).
  159. ↑ (en) Planck Collaboration Team, « Planck intermediate results. XXX. The angular power spectrum of polarized dust emission at intermediate and high Galactic latitudes », Astronomy & Astrophysics, vol. 586,‎ , A133 (DOI 10.1051/0004-6361/201425034, Bibcode 2016A&A...586A.133P, arXiv 1409.5738).
  160. ↑ (en) Dennis Overbye, « Study Confirms Criticism of Big Bang Finding », The New York Times,‎ (lire en ligne, consulté le ).
  161. ↑ a b c et d (en) « DMR Images », Goddard Flight Space Center, NASA, .
  162. ↑ Reeves et al. 2008, p. 62 et 50 (graphique).
  163. ↑ Silk 1997, p. 64-67.
  164. ↑ (en) K. T. Inoue et J. Silk, « Local Voids as the Origin of Large-Angle Cosmic Microwave Background Anomalies: The Effect of a Cosmological Constant », The Astrophysical Journal, vol. 664, no 2,‎ , p. 650–659 (DOI 10.1086/517603, Bibcode 2007ApJ...664..650I, arXiv astro-ph/0612347).
  165. ↑ (en) « Astronomy Picture of the Day », NASA, .
  166. ↑ (en) A. Kogut, C. Lineweaver, G. F. Smoot, C. L. Bennett, A. Banday, N. W. Boggess, E. S. Cheng, G. De Amici, D. J. Fixsen, G. Hinshaw, P. D. Jackson, M. Janssen, P. Keegstra, K. Loewenstein, P. Lubin, J. C. Mather, L. Tenorio, R. Weiss, D. T. Wilkinson et E. L. Wright, « Dipole Anisotropy in the COBE Differential Microwave Radiometers First-Year Sky Maps », The Astrophysical Journal, vol. 419,‎ , p. 1–6 (DOI 10.1086/173453, Bibcode 1993ApJ...419....1K, arXiv astro-ph/9312056).
  167. ↑ (en) N. Aghanim, C. Armitage-Caplan, M. Arnaud, M. Ashdown, F. Atrio-Barandela, J. Aumont, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, K. Benabed, A. Benoit-Lévy, J.-P. Bernard, M. Bersanelli, P. Bielewicz, J. Bobin, J. J. Bock, J. R. Bond, J. Borrill, F. R. Bouchet, M. Bridges, C. Burigana, R. C. Butler, J.-F. Cardoso, A. Catalano, A. Challinor, A. Chamballu, H. C. Chiang, L.-Y Chiang, P. R. Christensen et al., « Planck 2013 results. XXVII. Doppler boosting of the CMB: Eppur si muove », Astronomy & Astrophysics, vol. 571, no 27,‎ , A27 (DOI 10.1051/0004-6361/201321556, Bibcode 2014A&A...571A..27P, arXiv 1303.5087).
  168. ↑ Lachièze-Rey et Gunzig 1995, p. 197.
  169. ↑ Lachièze-Rey et Gunzig 1995, p. 90-91.
  170. ↑ (en) G. Rossmanith, C. Räth, A. J. Banday et G. Morfill, « Non-Gaussian Signatures in the five-year WMAP data as identified with isotropic scaling indices », Monthly Notices of the Royal Astronomical Society, vol. 399, no 4,‎ , p. 1921–1933 (DOI 10.1111/j.1365-2966.2009.15421.x, Bibcode 2009MNRAS.399.1921R, arXiv 0905.2854).
  171. ↑ (en) A. Bernui, B. Mota, M. J. Rebouças et R. Tavakol, « Mapping the large-scale anisotropy in the WMAP data », Astronomy and Astrophysics, vol. 464, no 2,‎ , p. 479–485 (DOI 10.1051/0004-6361:20065585, Bibcode 2007A&A...464..479B, arXiv astro-ph/0511666).
  172. ↑ (en) T.R. Jaffe, A. J. Banday, H. K. Eriksen, K. M. Górski et F. K. Hansen, « Evidence of vorticity and shear at large angular scales in the WMAP data: a violation of cosmological isotropy? », The Astrophysical Journal, vol. 629,‎ , L1–L4 (DOI 10.1086/444454, Bibcode 2005ApJ...629L...1J, arXiv astro-ph/0503213).
  173. ↑ Lachièze-Rey et Gunzig 1995, p. 192.
  174. ↑ Lachièze-Rey et Gunzig 1995, p. 192-194.
  175. ↑ (en) A. de Oliveira-Costa, Max Tegmark, Matias Zaldarriaga et Andrew Hamilton, « The significance of the largest scale CMB fluctuations in WMAP », Physical Review D, vol. 69, no 6,‎ , p. 063516 (DOI 10.1103/PhysRevD.69.063516, Bibcode 2004PhRvD..69f3516D, arXiv astro-ph/0307282).
  176. ↑ (en) D. J. Schwarz, Glenn D. Starkman, Dragan Huterer et Craig Copi, « Is the low-l microwave background cosmic? », Physical Review Letters, vol. 93, no 22,‎ , p. 221301 (DOI 10.1103/PhysRevLett.93.221301, Bibcode 2004PhRvL..93v1301S, arXiv astro-ph/0403353).
  177. ↑ (en) P. Bielewicz, K. M. Gorski et A. J. Banday, « Low-order multipole maps of CMB anisotropy derived from WMAP », Monthly Notices of the Royal Astronomical Society, vol. 355, no 4,‎ , p. 1283–1302 (DOI 10.1111/j.1365-2966.2004.08405.x, Bibcode 2004MNRAS.355.1283B, arXiv astro-ph/0405007).
  178. ↑ (en) A. Slosar et U. Seljak, « Assessing the effects of foregrounds and sky removal in WMAP », Physical Review D, vol. 70, no 8,‎ , p. 083002 (DOI 10.1103/PhysRevD.70.083002, Bibcode 2004PhRvD..70h3002S, arXiv astro-ph/0404567).
  179. ↑ (en) P. Bielewicz, H. K. Eriksen, A. J. Banday, K. M. Górski et P. B. Lilje, « Multipole vector anomalies in the first-year WMAP data: a cut-sky analysis », The Astrophysical Journal, vol. 635, no 2,‎ , p. 750–60 (DOI 10.1086/497263, Bibcode 2005ApJ...635..750B, arXiv astro-ph/0507186).
  180. ↑ (en) C.J. Copi, Dragan Huterer, D. J. Schwarz et G. D. Starkman, « On the large-angle anomalies of the microwave sky », Monthly Notices of the Royal Astronomical Society, vol. 367,‎ , p. 79–102 (DOI 10.1111/j.1365-2966.2005.09980.x, Bibcode 2006MNRAS.367...79C, arXiv astro-ph/0508047).
  181. ↑ (en) A. de Oliveira-Costa et M. Tegmark, « CMB multipole measurements in the presence of foregrounds », Physical Review D, vol. 74, no 2,‎ , p. 023005 (DOI 10.1103/PhysRevD.74.023005, Bibcode 2006PhRvD..74b3005D, arXiv astro-ph/0603369).
  182. ↑ (en) Hao Liu et Ti-Pei Li, « Improved CMB Map from WMAP Data », ArXiv,‎ (arXiv 0907.2731v3).
  183. ↑ (en) Utane Sawangwit et Tom Shanks, « Lambda-CDM and the WMAP Power Spectrum Beam Profile Sensitivity », ArXiv,‎ (arXiv 1006.1270v1).
  184. ↑ (en) Hao Liu, Shao-Lin Xiong et Ti-Pei Li, « Diagnosing Timing Error in WMAP Data », ArXiv,‎ (arXiv 1009.2701v1).
  185. ↑ (en) M. Tegmark, A. de Oliveira-Costa et A. Hamilton, « A high resolution foreground cleaned CMB map from WMAP », Physical Review D, vol. 68, no 12,‎ , p. 123523 (DOI 10.1103/PhysRevD.68.123523, Bibcode 2003PhRvD..68l3523T, arXiv astro-ph/0302496). Les auteurs affirment que le quadrupôle et l'octupôle sont les plus contaminés, reflet de l'influence de la morphologie galactique.
  186. ↑ (en) I. O'Dwyer, H. K. Eriksen, B. D. Wandelt, J. B. Jewell, D. L. Larson, K. M. Górski, A. J. Banday, S. Levin et P. B. Lilje, « Bayesian Power Spectrum Analysis of the First-Year Wilkinson Microwave Anisotropy Probe Data », Astrophysical Journal Letters, vol. 617, no 2,‎ , L99–L102 (DOI 10.1086/427386, Bibcode 2004ApJ...617L..99O, arXiv astro-ph/0407027).
  187. ↑ (en) Jacob Aron, « Planck shows almost perfect cosmos – plus axis of evil », New Scientist,‎ (lire en ligne).
  188. ↑ (en) Richard Fisher et Rachel Courtland, « Found: Hawking's initials written into the universe », New Scientist,‎ (lire en ligne).
  189. ↑ (en) « Episode 5: The Big Bang and Cosmic Microwave Background » [vidéo], Astronomy Cast, (entretien avec Pamela L. Gay).
  190. ↑ (en) Leonard Burtscher, « Can you see the CMB in your analog TV? », sur ileo.de, (consulté le ).
  191. ↑ (de) Timo Stein et Christopher Förster, « Astronomie und Praxis - Beobachtung: Kosmologie mit Kaninchendraht und Wasser », Spectrum,‎ (lire en ligne, consulté le ).
  192. ↑ (en) Jack Gelfand, « The Cosmic Microwave Radiometer. An Instrument for the Detection of the Cosmic Microwave Background for Amateurs », sur jgelfand.net, (consulté le ).
  193. ↑ Weinberg 1978, p. 154.
  194. ↑ (en) A. K. T. Assis et M. C. D. Neves, « History of the 2.7 K Temperature Prior to Penzias and Wilson », Apeiron, vol. 2, no 3,‎ , p. 79–87 (lire en ligne [PDF]).
  195. ↑ (en) « Planck's new cosmic recipe », ESA Science & Technology, .
  196. ↑ Barrow 1996, p. 170.
  197. ↑ (en) Frank Durham et Robert D. Purrington, Frame of the universe: a history of physical cosmology, Columbia University Press, , 193–209 p. (ISBN 0-231-05393-2).
  198. ↑ Silk 1997, p. 11.
  199. ↑ Lachièze-Rey et Gunzig 1995, p. 8, écrivent : « C'est ainsi que le FDC est pris comme un indice très convaincant en faveur des modèles de big bang. ».
  200. ↑ Weinberg 1978, p. 18.
  201. ↑ (en) D. Scott, « The Standard Cosmological Model », Canadian Journal of Physics, vol. 84,‎ , p. 419–435 (DOI 10.1139/P06-066, Bibcode 2006CaJPh..84..419S, arXiv astro-ph/0510731).
  202. ↑ Hladik 2017, p. 145.
  203. ↑ Reeves 1994, p. 127.
  204. ↑ (en) « Fondamental Physical Constants - The NIST Reference on Constants, Units, and Uncertainty », NIST, .
  205. ↑ Lachièze-Rey et Gunzig 1995, p. 74.
  206. ↑ (en) Robert H. Brandenberger, « Formation of Structure in the Universe », ArXiv,‎ , p. 8159 (Bibcode 1995astro.ph..8159B, arXiv astro-ph/9508159, lire en ligne [PDF]).
  207. ↑ (en) A. H. Guth, The Inflationary Universe: The Quest for a New Theory of Cosmic Origins, Basic Books, (ISBN 978-0201328400, OCLC 35701222), p. 186.
  208. ↑ (en) Alan Guth, The Inflationary Universe, Basic Books, (ISBN 0201328402), p. 23.
  209. ↑ (en) Paul J. Steinhardt et Neil Turok, Endless Universe: Beyond the Big Bang, Broadway Books, (ISBN 9780767915014, lire en ligne), p. 114.
  210. ↑ (en) Paul J. Steinhardt, « The Inflation Debate - Is the theory at the heart of modern cosmology deeply flawed? », Scientific American,‎ (lire en ligne [PDF]).
  211. ↑ (en) D. Cirigliano, H.J. de Vega et N. G. Sanchez, « Clarifying inflation models: The precise inflationary potential from effective field theory and the WMAP data », Physical Review D, vol. 71, no 10,‎ , p. 77–115 (DOI 10.1103/PhysRevD.71.103518, Bibcode 2005PhRvD..71j3518C, arXiv astro-ph/0412634).
  212. ↑ Lachièze-Rey et Gunzig 1995, p. 19.
  213. ↑ Bojowald 2013, p. 156.
  214. ↑ Weinberg 1978, p. 81.
  215. ↑ Reeves 2007, p. 74.
  216. ↑ Weinberg 1978, p. 71-73.
  217. ↑ (en) E. Gawiser et J. Silk, « The cosmic microwave background radiation », Physics Reports, vol. 333–334,‎ , p. 245–267 (DOI 10.1016/S0370-1573(00)00025-9, Bibcode 2000PhR...333..245G, arXiv astro-ph/0002044).
  218. ↑ (en) Andrew Grant, « Water reveals the universe’s temperature 12.9 billion years ago », Physics Today,‎ (DOI 10.1063/PT.6.1.20220215a, lire en ligne Accès libre, consulté le ).
  219. ↑ a et b (en) Dominik A. Riechers, Axel Weiss, Fabian Walter, Christopher L. Carilli, Pierre Cox et al., « Microwave background temperature at a redshift of 6.34 from H2O absorption », Nature, vol. 602,‎ , p. 58-62 (DOI 10.1038/s41586-021-04294-5, lire en ligne Accès libre, consulté le ).
  220. ↑ (en) D. J. Fixsen, « The Temperature of the Cosmic Microwave Background », The Astrophysical Journal, vol. 707, no 2,‎ , p. 916–920 (DOI 10.1088/0004-637X/707/2/916, Bibcode 2009ApJ...707..916F, arXiv 0911.1955).
  221. ↑ (en) G. F. Smoot, « Cosmic Microwave Background Radiation Anisotropies: Their Discovery and Utilization », Nobel Lecture, Fondation Nobel, (consulté le ).
  222. ↑ (en) P. Noterdaeme, P. Petitjean, R. Srianand, C. Ledoux et S. López, « The evolution of the cosmic microwave background temperature », Astronomy & Astrophysics, vol. 526,‎ , p. L7 (DOI 10.1051/0004-6361/201016140, Bibcode 2011A&A...526L...7N, arXiv 1012.3164).
  223. ↑ (en) Lawrence M. Krauss et Robert J. Scherrer, « The return of a static universe and the end of cosmology », General Relativity and Gravitation, vol. 39, no 10,‎ , p. 1545–1550 (DOI 10.1007/s10714-007-0472-9, Bibcode 2007GReGr..39.1545K, arXiv 0704.0221).
  224. ↑ (en) Fred C. Adams et Gregory Laughlin, « A dying universe: The long-term fate and evolution of astrophysical objects », Reviews of Modern Physics, vol. 69, no 2,‎ , p. 337–372 (DOI 10.1103/RevModPhys.69.337, Bibcode 1997RvMP...69..337A, arXiv astro-ph/9701131).
  225. ↑ Reeves 2007, p. 48-49.
  226. ↑ Reeves et al. 2008, p. 62-63.
  227. ↑ Silk 1997, p. 65-67.
  228. ↑ (en) Bob Yirka, « Scientists debate the seriousness of problems with the value of the Hubble Constant », Phys.org, .
  229. ↑ (en) Natalie Wolchover, « What Shape Is the Universe? A New Study Suggests We’ve Got It All Wrong », Quanta Magazine,
  230. ↑ (en) Eleonora Di Valentino, Alessandro Melchiorri et Joseph Silk, « Planck evidence for a closed Universe and a possible crisis for cosmology », Nature Astronomy,‎ (ISSN 2397-3366, DOI 10.1038/s41550-019-0906-9).
  231. ↑ « Parallax-e, Galerie d’art Foreman, Sherbrooke », Foreman, (le photomontage apparaît à la droite sur la première photo).
  232. ↑ (en + fr) Gentiane Bélanger, Jean-Pierre Aubé, Nicolas Baier, Laurent Grasso, Bettina Forget, Rachel Sussman, Semiconductor et Julie Tremble, Parallax-e, esse, (lire en ligne [PDF]), p. 6.

Voir aussi

modifier

Sur les autres projets Wikimedia :

Bibliographie

modifier

Document utilisé pour la rédaction de l’article : document utilisé comme source pour la rédaction de cet article.

Articles connexes

modifier

Moyens observationnels

Liens externes

modifier

Résultats

Aspects cosmologiques

Vulgarisation

Bases de données et dictionnaires

Cet article est reconnu comme « bon article » depuis sa version du 2 octobre 2018 (comparer avec la version actuelle).
Pour toute information complémentaire, consulter sa page de discussion et le vote l'ayant promu.
La version du 2 octobre 2018 de cet article a été reconnue comme « bon article », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.
Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Fond_diffus_cosmologique&oldid=218810062 ».