Solide d'Archimède
En géométrie, un solide d'Archimède est un polyèdre convexe semi-régulier, fortement symétrique, composé de deux ou trois sortes de polygones réguliers se rencontrant à des sommets identiques. Ils sont distincts des solides de Platon, qui sont composés d'une seule sorte de polygones se rencontrant à des sommets identiques, et des solides de Johnson, dont les faces polygonales régulières ne se rencontrent pas à des sommets identiques. La symétrie des solides d'Archimède exclut les membres du groupe diédral, les prismes et les antiprismes.
Les solides d'Archimède peuvent tous être construits via les constructions de Wythoff à partir des solides de Platon avec les symétries tétraédrique (en), octaédrique et icosaédrique. Voir polyèdre uniforme convexe.
Origine du nom
modifierLes solides d'Archimède tirent leurs noms du mathématicien grec Archimède, qui les étudia dans un ouvrage actuellement perdu. Pendant la Renaissance, les artistes et les mathématiciens ont évalué les formes pures et ont redécouvert toutes ces formes. Cette recherche fut complétée aux alentours de 1619 par Johannes Kepler, qui définit les prismes, les antiprismes et les solides réguliers non-convexes connus sous le nom de solides de Kepler-Poinsot.
Classification
modifierIl existe 13 solides d'Archimède (15 si l'on compte l'image chirale (dans un miroir) de deux solides énantiomorphes, décrits plus précisément ci-dessous). Dans cette table, la configuration de sommet fait référence au type de polygones réguliers que l'on rencontre à un sommet donné quelconque (symbole de Schläfli). Par exemple, une configuration de sommet de (4,6,8) signifie qu'un carré, un hexagone et un octogone se rencontrent à un sommet (avec l'ordre pris dans le sens horaire autour du sommet). Un quatorzième solide, la gyrobicoupole octogonale allongée, répond « presque » à la définition, en ce que tous ses sommets ont la même configuration de sommet, mais il n'est pas semi-régulier. Enfin, les familles infinies des prismes et des antiprismes ne sont généralement pas comptées comme solides d'Archimède, leur groupe de symétrie se réduisant à un groupe diédral.
Le nombre de sommets est 720° divisé par le défaut angulaire (en) au sommet[1].
| Nom | Solide | Faces | Arêtes | Sommets | nombre d'arêtes par sommet |
Configuration de sommet |
Groupe de symétrie |
Graphe squelette | |
|---|---|---|---|---|---|---|---|---|---|
| Tétraèdre tronqué | 
|
8 | 4 triangles 4 hexagones |
18 | 12 | 3 | 3,6,6 | Td | Graphe tétraédrique tronqué |
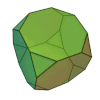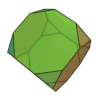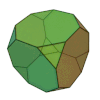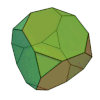
| Cube tronqué ou hexaèdre tronqué |
|
14 | 8 triangles 6 octogones |
36 | 24 | 3 | 3,8,8 | Oh | Graphe hexaédrique tronqué |
| Octaèdre tronqué | 
|
14 | 6 carrés 8 hexagones |
36 | 24 | 3 | 4,6,6 | Oh | Graphe octaédrique tronqué |
| Dodécaèdre tronqué | 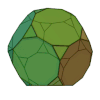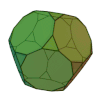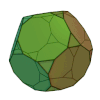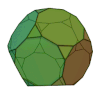
|
32 | 20 triangles 12 décagones |
90 | 60 | 3 | 3,10,10 | Ih | Graphe dodécaédrique tronqué |
| Icosaèdre tronqué ou Buckyball ou ballon de foot |

|
32 | 12 pentagones 20 hexagones |
90 | 60 | 3 | 5,6,6 | Ih | Graphe icosaédrique tronqué |
| Cuboctaèdre | 
|
14 | 8 triangles 6 carrés |
24 | 12 | 4 | 3,4,3,4 | Oh | Graphe cuboctaédrique |
| Cube adouci (2 formes chirales) |
 
|
38 | 32 triangles 6 carrés |
60 | 24 | 5 | 3,3,3,3,4 | O | Graphe cuboctaédrique adouci |
| Icosidodécaèdre | 
|
32 | 20 triangles 12 pentagones |
60 | 30 | 4 | 3,5,3,5 | Ih | Graphe icosidodécaédrique |
| Dodécaèdre adouci (2 formes chirales) |
 
|
92 | 80 triangles 12 pentagones |
150 | 60 | 5 | 3,3,3,3,5 | I | Graphe dodécaédrique adouci |
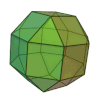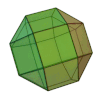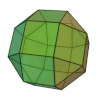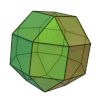
| Petit rhombicuboctaèdre |
|
26 | 8 triangles 18 carrés |
48 | 24 | 4 | 3,4,4,4 | Oh | Graphe rhombicuboctaédrique |
| Cuboctaèdre tronqué |

|
26 | 12 carrés 8 hexagones 6 octogones |
72 | 48 | 3 | 4,6,8 | Oh | Graphe cuboctaédrique tronqué |
| Petit rhombicosidodécaèdre ou rhombicosidodécaèdre |

|
62 | 20 triangles 30 carrés 12 pentagones |
120 | 60 | 4 | 3,4,5,4 | Ih | Graphe icosidodécaédrique tronqué |
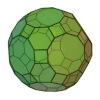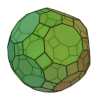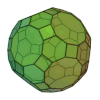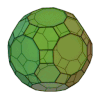
| Icosidodécaèdre tronqué |
|
62 | 30 carrés 20 hexagones 12 décagones |
180 | 120 | 3 | 4,6,10 | Ih | Graphe rhombicosidodécaédrique |
Le cuboctaèdre et l'icosidodécaèdre ont des arêtes uniformes et ont été appelés quasi-réguliers.
Le cube adouci et le dodécaèdre adouci sont chiraux, ils sont de deux formes, (lévomorphe et dextromorphe). Lorsqu'un objet possède plusieurs formes qui sont images miroir les unes des autres en trois dimensions, ces formes sont appelées énantiomorphes. (Cette nomenclature est aussi utilisée pour les formes de composés chimiques, voir énantiomère).
Les duaux des solides d'Archimède sont appelés les solides de Catalan. Avec les bipyramides et les trapèzoèdres, ce sont les solides à faces uniformes et sommets réguliers.
Notes et références
modifier- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Archimedean solid » (voir la liste des auteurs).
- (en) Eric W. Weisstein, « Descartes Total Angular Defect », sur MathWorld
Annexes
modifierBibliographie
modifier- (en) Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979 (ISBN 978-0-486-23729-9)
Articles connexes
modifier- Polyèdre semi-régulier
- Polyèdre uniforme
- Liste des polyèdres uniformes
- Symétroèdre
- Libellus de quinque corporibus regularibus de Piero della Francesca
- Trattato d'abaco de Piero della Francesca
Liens externes
modifier- (en) Eric W. Weisstein, « Archimedean Solid », sur MathWorld
- (en) Archimedean Solids and Catalan Solids sur software3d.com
- (en) Pictures of Archimedean Solids sur korthalsaltes.com
- (en) The Uniform Polyhedra sur mathconsult.ch
- (en) Virtual Polyhedra sur le site de George W. Hart (en)
- (en) Penultimate Modular Origami par James S. Plank, de l'université du Tennessee
- (en) Interactive polyhedra en Java sur ibiblio.org