Discussion:Hiérarchie de Chomsky

Exemples

Il faudrait en donner pour chaque type de grammaire pour montrer les impacts sur les raisonnements. L'exemple actuel est-il correct ? La "réponse" mériterait quelques explications, sur la question en particulier ! --JeanClem 23 mai 2006 à 11:00 (CEST)

Après avoir relu plusieurs fois ces explications, je reste incapable de jauger un langage pour dire à quelle grammaire il appartient. Je ne nie pas avoir quelques lacunes en mathématiques. Je cherchais à savoir à quel type appartiennent les langages de programmation C et C#. Impossible de faire le lien entre les formules mathématiques abstraites et ces cas concret. Il serait intéressant de donner, pour chaque type, le nom langage connu qui utilise cette grammaire, ou un exemple plus concret que les aaabbbaab+aa qu'on trouve sur tous les sites qui parlent de cette classification. Mose, 8 sept 2006

À améliorer

La définition était fausse pour le type 1 ! Il manque des exemples. Pour répondre à la question précédente, si un langage est engendré par une grammaire de type 2 (par exemple), ça veut dire qu'il est de type 2 (donc aussi de type 0 et 1), mais il est peut-être aussi de type 3, si on arrive à trouver une grammaire plus simple pour ce langage. Étant donné un langage, on ne peut pas toujours déterminer son type à coup sûr, par exemple savoir si un langage de type 2 est en fait de type 3 est indécidable. Pour beaucoup de langages de programmation, l'essentiel (du travail) se fait avec le type 2 : pour les expressions arithmétiques, les structures de contrôle (if-then-else, blocs, ...). Mais ils sont le plus souvent de type 1, parce que l'on doit déclarer toutes les variables avant de s'en servir, toutes les fonctions avant ou après qu'on s'en sert, ... Tchai 10 janvier 2007 à 17:26 (CET)

PS. En fait, il y a plus de détails à Grammaire_hors-contexte. Merci à Special:Contributions/194.199.184.126 qui a corrigé le lien. Tchai 26 avril 2007 à 16:39 (CEST)

Grammaires régulières == grammaires linéaires à droite ?

Mon prof de théorie des langages (cf son cours) considère que les grammaires régulières se limitent aux grammaires linéaires à droite. C'est aussi ce que j'ai trouvé ici et là. Je suis troublé. Arronax50 18 mars 2007 à 19:17 (CET)

C'est juste une convention. Ce qui est important, c'est de ne pas mélanger les règles de type gauche et droit. Mais les linéaires gauches et les linéaires droites ont exactement le même pouvoir d'expression, et il est facile de les transformer en automate fini... Tchai 20 mars 2007 à 14:56 (CET)

Merci de l'éclaircissement. Arronax50 20 mars 2007 à 18:19 (CET)

La formulation n'est pas claire pour moi. Il y a trois possibilités : soit les langages rationnels sont définis par les grammaires linéaires à gauche (et de manière équivalentes par les linéaires à droite), soit ils sont définis par les grammaires qui sont linéaires à gauche et à droite, soit mes deux premiers cas sont tous les deux vrais. En gros, un langage rationnel est-il défini par une grammaire contenant des règles A → a et A → Ba, ou faut-il trois types de règles A → a, A → Ba et A → aB, ou encore ces deux définitions sont équivalentes ? Grob (d) 30 septembre 2010 à 18:13 (CEST)

Problème de définitions

Dans certaines formules, l'article fait référence à $V$ ou $\Sigma$ sans les définir au préalable. Si j'ai bien compris, $V=N\cup T$ et $\Sigma =T$, mais il faudrait soit corriger, soit préciser.

--Tastalian 27 mai 2007 à 17:57 (CEST)

Certes. J'ai ajouté une phrase au début. Et j'ai déplacé cette discussion à la fin, pour respecter l'ordre usuel. --Tchai 28 mai 2007 à 09:59 (CEST)

Seule classification naturelle possible ?

Je suis étonné du paragraphe « La hiérarchie de Chomsky constitue la seule classification naturelle possible des grammaires génératives ; à chaque type de grammaire correspond un type d'automate. Il est formellement impossible de concevoir d'autres classes de grammaires comme d'autres classes d'automates. Comme pour la thèse de Church-Turing affirmant qu'il ne peut exister de langage supérieur à celui généré par la Machine de Turing, la division des automates et des grammaires en classes strictement disjointes est basée sur notre incapacité à créer un système logico-mathématique qui n'entrerait pas strictement dans une de ces classes. » C'est une affirmation philosophique, non fondée sur des sources, et contraire à la vérité scientifique: il existe des centaines de classes de langages et d'automates dans la littérature. La hiérarchie de Chomsky date de 50 ans, et cela se sent, ce qui n'enlève rien au mérite de Chomsky.

Le paragraphe de l'introduction que j’avais ajouté dans la version du 28 juillet: « La hiérarchie de Chomsky constitue une première approche de la classification des langages formels. Il est remarquable qu'à chaque type de grammaire correspond un type d'automate Depuis, de nombreuses autres classes de grammaires, de langages ,et d'automates ont été introduites, qui permettent de répondre mieux aux exigences de problèmes sépecifiques, comme la définition des langages de programmation ou la conception d’interpréteurs ou de compilateurs, ou encore l’analyse des langages naturels. » reflète cette appréciation. Je propose de la remettre en place.--ManiacParisien (d) 14 novembre 2011 à 07:05 (CET)

Absolument pas car c'est du n'importe quoi. Aucune autre classe de grammaire générative calculable ne fut inventée comme aucune autre classe d'automate. C'est justement le propre de la hiérarchie de Chomsky, il ne reste plus de place. Rien de plus puissant que la machine de Turing n'existe et nous sommes dans l'incapacité de concevoir un automate se plaçant entre deux catégories. Et ceci pour l'éternité, il s'agit d'une loi de la nature.

Désolé, mais c'est non.--Nipou (d) 15 novembre 2011 à 05:34 (CET)

Si tu veux dire quelque chose de pertinent, il faudrait entrer dans le domaine du non-calculable et ceci est très loin des interpréteurs et des compilateurs.--Nipou (d) 15 novembre 2011 à 05:38 (CET)

Les automates à pile déterministes se placent entre les context-free et les rationnels. Sont-ils contre nature??? Je voudrais avoir une seule référence à un ouvrage sérieux où on dit qu'il ne reste plus de place: ça, c'est vraiment nouveau!--ManiacParisien (d) 15 novembre 2011 à 06:58 (CET)

Si nouveau c'est cinquante ans comme tu l'as si bien dit... Les automates à piles déterministes acceptent exactement le langage des «context-free grammars», rien de plus, rien de moins. Il ne faut pas confondre classe disjointe de construction de classe hiérarchique de langage. Ils acceptent évidemment également les grammaires régulières car elles sont contenues dans les «context-free grammars». Mais il n'existe aucun système logico-mathématique acceptant quelque chose entre les deux comme tu dis.--Nipou (d) 15 novembre 2011 à 10:37 (CET)

En fait, lorsque nous allons entre deux classes nous sombrons dans l'incalculable commme les Automate de Büchi qui se trouvent légèrement entre l'automate à pile et les grammaires régulières. Il s'agit de langages infinis par contre, rien de concret dans le monde réel.--Nipou (d) 15 novembre 2011 à 10:53 (CET)

Ici, lorsque l'on parle d'être entre les deux, c'est une analogie de forme syntaxique. Ceci n'a rien à voir avec les mots du langage. Il n'existe aucun système logico-mathématique acceptant un sous ensemble des langages des grammaires régulières union un sous-ensemble des langages des grammaires hors-contextes. Si on veux le faire, il faut créer une fonction calculable f qui nécessite l'existence de lambda pour exister, soit lambda f. Nous avons donc besoins de la machine de Turing et nous nous trouvons alors dans les langages récursifs.--Nipou (d) 15 novembre 2011 à 23:12 (CET)

Je suis très ennuyé. D'abord, techniquement: les automates à pile déterministes n'acceptent pas tous les langages context-free. Si j'ai parlé de ces automates, c'est qu'ils sont importants en compilation. Mais je vois qu'il n'est pas vraiment possible de discuter avec vous. Aucune autre page sur la hiérarchie de Chomsky, que ce soit en anglais, en allemand, en finlandais ou autre, contient de telles affirmations logico-philosophiques non sourcées. Pour l'image de sérieux des pages francophones, on ne peut pas admettre cela! --ManiacParisien (d) 16 novembre 2011 à 07:14 (CET)

Je sais que c'est difficile d'admettre qu'on a complètement tort. Sur la page Automate à pile, il y a la proposition « Les langages acceptés par les automates à piles sont exactement les langages algébriques, c'est-à-dire ceux engendrés par une grammaire algébrique. » sur la page Langage algébrique, nous avons «En théorie des langages formels, un langage algébrique ou langage non contextuel...». Évidemment, c'est difficile de discuter quand on se fait constemment planter... désolé... mais ce n'est pas une guerre de pouvoir, que d'autorité.

Eviter les provocations SVP. Encore une fois, la discussion serait plus simple si le paragraphe en question était soigneusement sourcé. Voir ci-dessous. Il y a peut-être des quiproquos, impossible à élucider si on ne se réfère pas aux sources pour voir exactement ce que le rédacteur a voulu dire. --Jean-Christophe BENOIST (d) 16 novembre 2011 à 17:21 (CET)

OK, mais je n'ais pas de livre chez moi, que dans le sous-sol de chez mon père... probablement rongés par les vers...je vais faire des recherche sur le web.--Nipou (d) 17 novembre 2011 à 01:59 (CET)

Je vais regarder cela à tête reposée, mais - d'ores et déjà - est-ce qu'il serait possible de sourcer plus précisément, à la manière de Problème P = NP ou de Nombre Oméga par exemple, en sourçant les phrases, ou les membres de phrases clés, et en indiquant la page ou le paragraphe dans chaque source ? Je pense que c'est une pratique absolument indispensable, et qui pourrait simplifier la discussion. Ici, c'est le paragraphe qui est sourcé globalement, par un ensemble de bouquins désignés globalement. Difficile de faire plus imprécis. --Jean-Christophe BENOIST (d) 16 novembre 2011 à 09:33 (CET)

Hiérarchie de Chomsky et autres trucs liés à la calculabilité

(Un peu en lien avec la section ci-dessus) Placé sur la page de discussion de nipou le 9 novembre 2011.

Bonjour Nipou, j'ai l'impression qu'un désaccord se crée sur cet article sur tout simplement 2 aspects complémentaires 1/ Cette hiérarchie de Chomsky est indépassable (si on accepte l'hypothèse de Church) en ce qui concerne les langages calculables (= machines de Turing) 2/ évidemment cette hiérarchie n'est pas la seule et il y a plus élevé comme la hiérarchie arithmétique, vu qu'évidemment tout n'est pas calculable/décidable (= pb de l'arrêt des machines de Turing). A mon sens il faudrait parler de cela (sujet pas si simple) en essayant d'être précis dans les termes utilisés grammaires- automates - langages (termes informels qui ne sont pas équivalents selon les contextes formels où ils sont utilisés). Aussi concernant cette hiérarchie de Chomsky des liens seraient à mettre avec les notions de récursivement énumérable et d'ensemble récursif. Cordialement. --Epsilon0 ε₀ 9 novembre 2011 à 00:35 (CET)

Il faudrait distinguer la conception constructiviste de l'approche par oracle non-déterministe et des hiérarchies de langages non-calculables. Séparer le réel de la réflexion sur le réel.

Par contre, au niveau de l'informatique appliquée, la hiérarchie de Chomsky et la thèse de Church sont des phénomènes de la nature avec lesquels nous devons vivre.

--Nipou (d) 10 novembre 2011 à 03:01 (CET)

Je ne suis pas spécialiste de ces questions, mais informaticien. Il me semble qu'une classe de problèmes peut naitre de l'interactivité (jeu d'échec, pilotage …). Si un automate basé sur une grammaire met du temps à aboutir et qu'une intervention extérieure modifie l'objectif pendant le calcul, le résultat n'est plus seulement du aux conditions initiales. Il a-t-il alors de nouvelles classes ? Est-ce prévu par la théorie ? --Rical (d) 16 novembre 2011 à 16:37 (CET)

Soit on considère "l'intervention extérieure" comme un automate, dans ce cas nous avons affaire à un automate qui appelle un autre automate, donc nous avons globalement une machine de Turing. Soit on considère "l'intervention extérieure" comme n'étant pas modélisable par un automate, dans ce cas nous avons une machine de Turing avec Oracle. En revanche, je ne sais pas ce qu'il en est des hiérarchies avec les MTO. --Jean-Christophe BENOIST (d) 16 novembre 2011 à 17:02 (CET)

Oui, mais léger bémol, pour que l'oracle naturel existe, il faut une démonstration formelle que cet oracle ne soit pas calculable par machine de Turing. Ce qui n'est le cas d'aucun phénomène naturel connu... du moins avec certitude. Le jugement expert humain ne peut certainement pas être considéré comme tel... du moins, pas le jugement raisonnable.--Nipou (d) 19 novembre 2011 à 00:12 (CET)

Ma théorie personnelle sur cette question est que prédire la trajectoire de n'importe quel électron implique de connaitre toutes les influences de tout l'univers, et toutes les théories scientifiques même futures capables de l'expliquer. Toutes les théories sont des croyances provisoires et la complexité du raisonnement humain est si rudimentaire qu'il serait prétentieux de croire que nous pourrons un jour tout savoir. J'en conclue que la nature est surement au delà de la porté des automates que les humains sont capables de concevoir et je serais bien étonné qu'aucun chercheur n'ait pensé à cela. Et il y a aussi le principe d'incertitude d'Eisenberg, les aléas quantiques, la théorie du chaos et les problèmes NP complets. --Rical (d) 19 novembre 2011 à 11:13 (CET)

Nous commençons à être bien loin de la hiérarchie de Chomsky et du sujet de l'article ! Et là est le fond du problème d'ailleurs, pour revenir au sujet du désaccord sur cet article. En fait, le problème n'est pas de savoir si la hérarchie de Chomsky est dépassable ou non avec des machines de Turing; la réponse est simple : non. Le problème est de savoir si on peut en tirer des conséquences métaphysiques et comment le formuler/sourcer. Tout le problème du passage est l'emploi des mots "naturelle", et surtout dénier la possibilité de conçevoir (dans l'absolu) d'autres hiérarchies, qui "n'existeraient" pas car le l'univers ne serait qu'une vaste machine de Turing. Je vais essayer de reformuler le paragraphe, qui contient du vrai, en le débarassant des aspects métaphysiques, qui ne me semblent d'ailleurs pas sourcés par les sources globales mises. Je possède certaines d'entre-elles, et dans celles que je possède il n'est absolument pas question des aspects méthaphysiques. --Jean-Christophe BENOIST (d) 19 novembre 2011 à 16:06 (CET)

J'ai des doutes sur la dernière phrase du paragraphe : je ne vois pas en quoi l'imbrication est fondée sur la non-existence de langage calculable d'ordre supérieur. Si la thèse de Church était fausse et qu'il existe un langage calculable d'ordre supérieur, qui incluerait ceux générés par le MT, il existerait toujours une imbrication. Mais j'ai peut-être mal compris le "message" de cette phrase (d'où l'utilité de sourcer pour vérifier ce qu'a voulu dire l'auteur !). Je met un "refnec" particulièrement sur cette phrase. Quel est le "message" de cette phrase exactement ? --Jean-Christophe BENOIST (d) 19 novembre 2011 à 16:26 (CET)

Parce qu'elle ne l'est pas, tout simplement.

Le hiérarchie de Chomsky est basée sur le même mécanisme que la thèse de Church mais ils sont sans le moindre autre rapport mathématique que ce rapprochement technique : celui de l'incapacité humaine à créer un système.--Nipou (d) 20 novembre 2011 à 00:30 (CET)

Arrête de parler d'"incapacité humaine"^{[réf. nécessaire]}, cela ne veut rien dire. Donc, la notion d'imbrication n'est pas centrale dans cette phrase ? Je vais essayer de la reformuler sans spécialement parler d'imbrication, ce qui met sur une mauvaise piste, et transformer le "refnec" en "refsou" car ce parallèle n'est fait par aucune source à ma connaissance. --Jean-Christophe BENOIST (d) 20 novembre 2011 à 00:36 (CET)

Pour le "refsou" je serais aussi intéressé de voir une source car la suite immédiate de la phrase la hiérarchie des classes de grammaire mène à la thèse qu'il n'existe pas de langage calculable qui n'entre pas strictement dans une de ces classes semble d'emblée l'infirmer. Je précise que je dis cela en simple lecteur connaissant fort mal les classifications au sein du calculable. D'ailleurs me vient une question : les fonctions primitives récursives se classent où dans cette hiérarchie de Chomsky ? --Epsilon0 ε₀ 20 novembre 2011 à 01:40 (CET)

C'est une bonne question, pas du tout discutée dans les sources que je possède d'ailleurs. Après une recherche, les sources semblent bizarrement discordantes. [1] identifie strictement les primitives récursives aux langages de type 1 (context-sensitif), tandis que [2] par exemple (p. 588), résume les résultats de Gold [1967] dans la hiérarchie : Finite < Superfinite < Regular < Context-free < Context-sensitive < Primitive Recursive < Recursive < Recursively Enumerable. Un point à élucider, et à reporter dans l'article si cela devient clair. --Jean-Christophe BENOIST (d) 20 novembre 2011 à 12:48 (CET)

La notion de calculable comprenant le récursivement énumérable est en premier lieu complètement abusif; j'en suis conscient. Je n’aie jamais vu de hiérarchie de Chomsky décomposant le récursivement énumérable avec des hiérarchies non-calculables que je connais très mal et l'univers avec des oracles. Par contre, une telle décomposition serait magnifique.

En ce qui concerne la notion «d'incapacité humaine», elle est équivalente à la position psychologique de la thèse de Church-Turing et effectivement, il s'agit d'une position que je n'accepte pas du tout mais qui est la plus répandue.

--Nipou (d) 20 novembre 2011 à 21:20 (CET)

Hiérarchie de Chomsky et autres trucs liés à la calculabilité (partie 2)

En attendant d'être sourcée, je serais d'avis de supprimer la phrase en "refsou" dans l'intro, étant donné qu'Epsilon a émis un doute, et que finalement cette phrase a été reformulée par moi sans que je sois sûr d'avoir bien compris et retranscrit l'idée initiale de la phrase. Une source permettrait de comprendre exactement l'idée, et de s'assurer que l'association entre thèse de CT et hiérarchie de Chomsky n'est pas inédite. Des avis ? --Jean-Christophe BENOIST (d) 22 novembre 2011 à 22:04 (CET)

Je suis d'accord avec cette proposition. Les deux phrases qui précèdent disent - si j'ai bien compris - qu'on ne peut concevoir des classes supplémentaires; ceci semble en contradiction avec l'ajout des classes récursives, primitives récursives, tree adjunct etc. Peut-on préciser cela. Il existe aussi des classes transversales, comme les systèmes de Lindenmayer, ou les "splicing systems" biologiques qui ne s'insèrent pas proprement dans la hiérarchie. Mais peut-être là aussi, je n'ai pas bien compris la notion de "seule classification possible"?--ManiacParisien (d) 23 novembre 2011 à 18:54 (CET)

L'idée du paragraphe est plutôt de dire, je crois, que 1) il n'existe pas d'autres classes, ou classification, du calculable qui ne soient pas strictement incluses dans les classes de Chomsky, pas qu'il n'existe pas d'autres partitions possibles du calculable, et 2) que si on adopte la classification de Chomsky, il est impossible d'étendre cette hiérarchie sans "dépasser" du calculable. En l'écrivant comme cela, cela me donne des idées de reformulation du paragraphe et de la phrase en question, pour résoudre cette ambiguïté que tu soulèves à juste titre. --Jean-Christophe BENOIST (d) 23 novembre 2011 à 22:29 (CET)

Bon moi aussi je ne suis pas sûr de bien comprendre la phrase en question ni même l'échange un peu elliptique ci-dessus. Néanmoins j'approuve le désir de Jean-Christophe de reformuler le paragraphe en me doutant qu'après ce sera mieux que ce qu'il y avait avant (qui était peu clair). Pis si après il nous reste des scrupules on pourra en rediscuter ici. Bien à vous. --Epsilon0 ε₀ 24 novembre 2011 à 00:25 (CET)

Il n’existe pas de système transversal, un système nécessite lambda ou pas et a lui même la puissance de lambda ou pas.

Si on a lambda on peut créer toute sorte de hiérarchies de langages, il s’agit de la « Mathématique » ; les groupes de Lie sont un bel exemple.

Il est possible de distinguer la mathématique « finie » de la mathématique « transcendantale» (voir Philippe Lauria, Cantor et le transfini: mathématique et ontologie).

La mathématique finie est celle régissant les langages récursifs soit l’informatique avec les nombres flottants et l’induction finie (si une propriété est vraie pour toute structure de taille N et implique qu'elle est également vraie pour toute structure de taille N+1 alors elle est vraie pour toute structure de taille finie).

La mathématique transcendantale est celle régissant le récursivement énumérable, on retrouve ici les nombres réels calculables (qui n’ont de réel que leur nom) et l’induction transfinie.

Les L-Systems sont intéressants car en plus d’être Turing-complets, ils révèlent axiomatiquement la hiérarchie de Chomsky.--Nipou (d) 26 novembre 2011 à 20:33 (CET)

N.B. : Nous entendons comme acquis que la « Mathématique » est l’ensemble des systèmes formalisables (axiomatisables) avec des systèmes de réécriture(grammaires génératives en linguistique) comme les Principia Mathematica.--Nipou (d) 26 novembre 2011 à 21:56 (CET)

Automate à pile et grammaire hors contexte

• Les langages hors contexte déterministes sont reconnus par les automates à pile déterministes.
• Les langages hors contexte sont reconnus par les automates à pile non-déterministes (Automates à pile).

Ici, le non-déterminisme indique simplement que le système peut se trouver dans plusieurs états en même temps, ce qui est très facile à implémenter.--Nipou (d) 18 novembre 2011 à 05:35 (CET)

Hiérarchie de Chomsky: derniers commentaires

Bravo pour cette tentative de rabibocher les choses. Je ne suis pas d'accord avec les phrases ou les mots suivants:

1. La hiérarchie de Chomsky constitue une classification complète des grammaires génératives: c'est le complet qui est en contradiction avec les exemples qui suivent.

Elle est complète du moment ou nous ne possédons pas de système n’acceptant (automate) ou ne générant (réécriture) pas strictement une des classes de langages connus.

Les découvertes actuelles s’effectuent à la frontière de la machine de Turing, les classes inférieures (supérieures dans la numérotation de Chomsky) sont clauses (sauf miracle), nous avons fait le tour de la question.--Nipou (d) 27 novembre 2011 à 18:50 (CET)

1. Il est formellement impossible de concevoir d'autres classes de grammaires comme des classes d'automates. C'est faux, et contredit par les exemples. Ce que l'auteur veut peut-être dire (mis ce n'est pas au lecteur d'essayer d'interpréter) c'est que il n'y a pas de grammaires génératives (ou de calculable) au delà de la forme générale, ce qui revient à ne rien dire: la forme générale est la forme sans restriction!

Je veux signifier qu’il n’existe pas de système transversal connu. Nous en avons aucune démonstration par contre, il s’agit d’une conjecture. Nous pourrions considérer que la hiérarchie des monoïdes des L-Systems révèle la hiérarchie de Chomsky ; mais il ne s’agit aucunement d’une démonstration couvrant l’ensemble des sous-systèmes imaginables de la machine de Turing (ou système de réécriture). --Nipou (d) 27 novembre 2011 à 18:50 (CET)

1. U est l'univers de tous les langages de mots finis et infinis possibles. Ce sont tous les langages, finis ou infinis, de mots: les mots infinis n'on rien à voir là dedans, je pense.

Ben voyons...

En fait c'est pareil...c'est le problème de l'axiome du choix (lemme de Zorn).

--Nipou (d) 27 novembre 2011 à 18:50 (CET)

1. densité d'incomplétude, soit le rapport de la cardinalité du dénombrable sur celui de l'indénombrable. Je ne sais pas ce que c'est l'indénombrable. L'ensemble de tous les langages a la puissance du continu, alors qu'il n'y a qu'un nombre dénombrable de machine de Turing: pas besoin de limite ni de densité.

Il faudrait demander à un transcendantaliste, epsilon0 semble connaître ce sujet. Puissance du continu (aleph0) c'est correct mais de plus en plus cryptique.

1. langages hors contexte déterministes: c'est un exemple qui vient ici comme un cheveu sur la soupe. C'était juste un exemple que je pensais utile à un moment de la discussion.

1. les machines de Turing en un temps fini (langages récursifs) et ceux acceptés en un temps infini (récursivement énumérables). Attention à la formulation; un langage accepté en un temps infini, je me demande ce que cela veut dire! Il y a des articles sur Wikipédia auxquels il vaut mieux se référer au lieu de les paraphraser de manière imagée, et fausse.

Un nombre de changement d'état infini dénombrable si tu préfères. Nous avons ici sur le ruban, de longueur infini, les nombres réels calculables.--Nipou (d) 27 novembre 2011 à 18:50 (CET)

1. les automates à pile embarquée. Malgré une recherche sur Google, je ne trouve pas ces automates. Les linguistes utilisent pourtant les grammaires citées.

Regarde sur Wiki anglais : "Embedded pushdown automaton". --Nipou (d) 27 novembre 2011 à 18:50 (CET)

1. Cette découverte permis de clarifier la frontière de la machine de Turing et de créer de nouvelles grammaires : linéaires, indexées, etc. Je ne sais pas où passe la frontière, mais certainement pas ici!. Par ailleurs, les grammaires linéaires existent depuis les années 50, les grammaires indexées existent depuis 1965 environ, donc historique, l'enchaînement est faux. Il n'y a d'ailleurs aucune raison de mettre en avant les grammaires à arbres adjoints.

Pas du tout, découvrir ce n'est pas comprendre...

1. Les langages sensibles au contexte semblent se diviser encore (grammaire sensible au contexte croissante). Je pense que la terminologie grammaire contextuelle est meilleure. Dans l'article correspondant, le lien avec les grammaires croissantes est, je crois, bien décrit.

Bref, cette introduction manque de rigueur, d'exactitude, de renvois. Et elle est encore truffée d'erreurs. Je ne peux donc pas y souscrire.

Pour la traduction française c'est comme tu veux, j'improvise à partir des termes anglais mais les grammaires contextuelles ne sont pas les grammaires sensibles au contexte croissante.--Nipou (d) 27 novembre 2011 à 18:50 (CET)

Pour être positif, pourquoi ne pas simplement traduire l'introduction de la version anglaise, allemande, italienne ou autre ?

Si elles sont fausses ça ne nous avance pas du tout. En fait, il n'en dise rien du tout.

Que dis-tu de cette version : «La hiérarchie de Chomsky est une conjecture affirmant que tout système formel ne génère ou n'accepte strictement qu'un des langages de la hiérarchie. Les langages de la hiérarchie étant imbriqués, un langage supérieur (numéro inférieur dans la notation de Chomsky) comprend les langages inférieurs.»

--ManiacParisien (d) 27 novembre 2011 à 14:43 (CET)

Super tableau de la hiérarchie

Les anglais ont un super tableau de la hiérarchie avec le template {{Formal languages and grammars}}. J'accepte ce tableau, il est complet (il faudrait commencer par s'entendre sur la hiérarchie). Ce tableau est disponible sur les différentes pages d'automates comme "Embedded pushdown automaton". --Nipou (d) 27 novembre 2011 à 19:09 (CET)

Introduction (again)

Encore une fois, les ajouts de Nipou sont absolument non sourcés, et de nombreuses phrases méritent pourtant vérification. La liaison avec la thèse de Church est encore mentionnée, et le fait de dire que la classe qui porte le n° zéro (et donc sous-entendu, il ne peut en exister une de n° inférieur) qui correspond à la machine de Turing est une explicitation de la thèse de Church, est peut-être juste et une véritable intention de Chomsky, mais cela peut être aussi absolument involontaire et sans cette intention. Peut-être que Chomsky s'est dit : je vais structurer les langages acceptés par une MT, et je pars donc de cette classe et lui donne le n° 0.

En parler comme d'une conjecture me parait aussi bizarre : cette hiérarchie est démontrée. Ce qui est une conjecture serait que cette hiérarchie est unique, totale etc.. mais ce n'est pas ce que dis Chomsky à ma connaissance. Chomsky s'est contenté de structurer et démontrer cette structuration, mais je ne sais pas, et je ne pense pas, que Chomsky ait conjecturé des choses en liaison avec le concept de calculabilité, ou sur l'unicité etc.. Dans aucune de mes sources n'apparait cela.

Je pense avec MP que l'introduction devrait être la plus factuelle possible et la plus courte possible, un peu à l'image des autres interwikis. Toute phrase allant au delà du factuel et étant une interprétation de la hiérarchie de Chomsky devrait être sourcée. Il est dommage qu'il faille encore le dire. --Jean-Christophe BENOIST (d) 2 décembre 2011 à 16:50 (CET)

Clairement l'introduction est à revoir car plombée d'intentions de démontrer des choses qui ne sont pas sourcées voire que l'on peut démontrer/sourcer comme fausses. Je tente dans la nouvelle section ci-dessous de faire un petit bilan sur cette hiérarchie, telle vue dans le Hopcroft et Ullman. --Epsilon0 ε₀ 2 décembre 2011 à 23:33 (CET)

Tentative de clarification avec le Hopcroft et Ullman

Bonjour, pour tenter de comprendre un peu j'ai consulté la bible de 1979 à savoir, John_E._Hopcroft,_Jeffrey_D._Ullman, Introduction to Automata Theory, Languages and Computation, Chap. 9, The Chomsky Hierarchy, pp.217-232

Mon propos ci-dessous ne concerne que cet ouvrage de 1979, j'imagine que des résultats nouveaux ont pu être exposés depuis.

On comprend que la hierarchie de Chomsky en terme de grammaire est une formulation de hiérachies au sein du calculable parmi d'autres (en termes de langage , d' automate/machine etc) qui à ce stade du livre (c'est le chap. 9) permet de définir une nouvelle classe non encore définie qui sera la classe 1.

• Le chapitre donne les équivalences suivantes (je garde la terminologie en anglais utilisée dans ce livre pour éviter d'éventuelles ambiguïtés) :
  • Type 0 = Machines de Turing = ensembles récursivement énumérable (r.e.) = r.e. language
  • Type 1 = Context sensitive language (CSF) = Context sensitive Grammar (CSG) = Linear bounded automaton (LBA°
  • Type 2 = Context free language (CFL)
  • Type 3 = Regular set = regular grammars = automates finis

Et on a page 228,

• The hierarchie theorem :
  • (a) The regular sets are properly contained in the context-free languages
  • (b) The CFL's not containing the empty string are properly contained in the context-sensitive languages. [je souligne]
  • (c) The CSL's are properly contained in the r.e. sets

Pour l'instant on a bien 4 classes bien étanches (mais remarquez la nuance que j'ai soulignée en (b) ) entre trucs aux définitions variées, et remarquez aussi 1/que rien ne dit qu'il n'existe pas de classes intermédiaires et 2/ que cette hiérarchie en 4 types est relative à la formulation en seul terme de grammaire.

• Maintenant dans le chapitre 10, Deterministic context-free language, on a dès l'intro :
  • However, for pushdown automata, we do know that the deterministic PDA's accept a family of languages, the deterministic context-free languages (DCFL's), lying properly between the regular sets and the context-free languages. [je souligne]
  • Bon je m'arrête là, on a donc qqch d'intermédiaire entre le type 3 et le type 2.
  • Cela met donc fin à l'affirmation de Nipou (d · c · b) pensant que la hiérarchie de Chomsky cerne toutes les classes possibles au sein du calculable.

Maintenant il faut que l'article soit recentré sur cette seule hiérarchie de Chomsky (qui est relative et aux grammaires, et à celles qu'il a définies et sans même preuve à ce que j'ai pu voir que des classes intermédiaires au sein de ces seules grammaires n'existent pas) tout en en montrant les équivalences mises ci-dessus et en en montrant aussi les limites. D'autres articles de wp peuvent explorer les autres hiérarchies, tjs au sein du calculable, mentionnées dans ce livre ou éventuellement nouvellement trouvées depuis 1979. Perso, ce travail ne m'intéresse guère car cette foultitude de def en tout sens me donne le tournis ;-). Mais m'intéressait de savoir si cette hiérarchie cernait le tout du calculable ; la réponse est donc NON.

Voilou, et vu que je possède l'ouvrage (sous format numérique ...) je reste à votre disposition si vous souhaitez des précisions.

p.s. : Si au hasard de vos recherches vous trouvez des trucs liés à cette hiérarchie ou d'autres concernant les fonctions primitives récursives (donc sans la Fonction d'Ackermann pour exemple) ce serait gentil de m'en faire part sur ma pdd ou par courriel. --Epsilon0 ε₀ 2 décembre 2011 à 23:30 (CET)

Je crois qu'un article peut très bien vivre avec une banderole questionnant la pertinence... mais franchement, c'est n'importe quoi... j’abandonne. Et vraiment, Epsilon0, je crois que la hiérarchie de Chomsky est trop concrète et terre à terre pour toi.--Nipou (d) 3 décembre 2011 à 01:46 (CET)

Gné, mais de quoi parles-tu ? Je suis totalement dans le terre-à-terre de cette hiérarchie que j'avoue ci-dessus très peu connaître et nullement dominer ; je constate simplement lors d'une petite investigation que très concrètement cette hiérarchie n'est pas le tout du calculable (car il y a au moins un truc entre le type 2 et le type 3). Sinon je ne vois pas en quoi on peut se satisfaire d'une banderole permanente exprimant que l'article est à améliorer ni en quoi il y aurait du n'importe quoi dans la démarche de MP, J-C B ou moi de tenter de cerner précisément l'état des connaissances sur le sujet. Nous sommes (enfin je parle pour moi) p.-e. bcp plus terre-à-terre que toi, espérant des envolées lyriques d'autant plus hautes que si la base est ferme ; mais pb : la terre est dure à labourer et le ciel est haut. --Epsilon0 ε₀ 3 décembre 2011 à 02:49 (CET)

Le but de ce bandeau n'est pas "de vivre avec", mais de signaler au lecteur que l'article est dans une version contestée et que un consensus est en cours de recherche en PdD. Ce qui est n'importe quoi n'est pas d'avertir le lecteur de prendre l'article avec des pincettes, mais de contribuer sans sources alors que ses ajouts ont de nombreuses fois été contestés.

Sinon, sur les sources. J'ai la version 2000 du Hopcroft/Ullman, mais le chapitre sur la hiérarchie de Chomsky a malheureusement disparu. Je n'ai donc pas l'original du texte, mais ce que cite Epsilon me semble suffisant pour discuter.

Il y a un point que je ne comprends pas dans ce que tu dis, Epsilon. Il y a deux choses différentes 1) La HC cerne tout le calculable, c'est à dire que tout langage calculable tombe dans une des classes de Chomsky 2) Les classes de la HC sont les seules classes envisageables, et/ou la seule hiérarchie envisageable du calculable. 1) peut être vrai et 2) faux simultanément. Les exemples que tu cites du H/U semblent dire que 2) est faux, c'est à dire qu'il existe des classes (p. ex. celle correspondant aux PDA déterministes) qui sont intermédiaires aux classes de Chomsky.

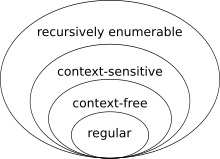
Mais tu sembles en conclure que 1) est faux (« Mais m'intéressait de savoir si cette hiérarchie cernait le tout du calculable ; la réponse est donc NON », ce qui ne me semble pas correct, en tout cas dans la définition que j'ai donné en 1) de "cerner le calculable". D'ailleurs la figure ci-contre ne montre aucun interstice entre les classes dans lesquels un langage calculable pourrait se loger. Pourrais-tu éclaircir ta position ?

Quoi qu'il en soit, cela montre que dès que l'on parle de propriétés générales (la HC cerne le calculable (ou non), traduit la thèse de Church etc..) il est indispensable d'avoir une source qui dise cela explicitement : on ne peut pas se permettre de faire des déductions non sourcées, même si elles sont justes. --Jean-Christophe BENOIST (d) 3 décembre 2011 à 11:59 (CET)

PS : voir (comme l'avait signalé Nipou) en:Template:Formal languages and grammars, où l'on voit que - comme le dit le H/U - la classe des langages acceptés par les PDA déterministes est intermédiaire entre 2 et 3, mais incluse dans le type 2, et ne remet pas en cause la "complétude" de la hiérarchie de Chomsky. --Jean-Christophe BENOIST (d) 3 décembre 2011 à 13:05 (CET)

Ma phrase était en effet peu claire, je voulais bien dire que 1) est vrai et 2) est faux. --Epsilon0 ε₀ 3 décembre 2011 à 16:15 (CET)

La notion de «cerner le calculable» ne veut rien dire; la hiérarchie de Chomsky exprime simplement le fait que toute tentative de créer un système formel concret (calculable) le fait tomber dans une des classes de la hiérarchie. Plus aucun auteur moderne ne présente la hiérarchie de Chomsky avec quatre ou cinq classes, la hiérarchie de Chomsky évolue avec la découverte de systèmes formels (inférieur à la machine de Turing, évidemment) ajoutant une couche à l’oignon. Ce qui est bizarre c'est l'inexistence d'un système transversal, même avec les nouvelles découvertes, l'oignon de Chomsky reste un oignon (aucun système ne génère seulement un sous-ensemble du régulier et du sensible au contexte sans générer le hors contexte, par exemple).

Ce qui m'a fait vraiment capoter c'est le faux problème du mot vide... je croyais vraiment qu'epsilon0 mettait ceci de l'avant pour prouver que les automates inférieurs n'acceptaient pas l'ensemble du calculable.

En fait, tout automate déterministe acceptant le mot vide n'accepte rien d'autre (essayez d'écrire un programme s'arrêtant sur l'absence de frappe au clavier et également sur un mot quelconque). Le mot vide ne peut être accepté que par un automate acceptant les changements d'états spontanés (transition spontané sans lecture d'un caractère). Le plus amusant est que le mot vide est très évidemment un problème entre le métalangage de la théorie des ensembles et le langage généré ou accepté par le système. La description du mot vide dans le métalangage nécessite la répétition d'un caractère comme "" ou de deux caractères spéciaux comme [] ou {}; symboles évidemment inconnus du système formel étudié.--Nipou (d) 7 décembre 2011 à 02:17 (CET)

Encore mon grain de sel.

(1) Il existe bien entendu des automates déterministes qui acceptent le mot vide et autre chose: simplement l'automate à un seul état qui accepte tous les mots (et donc aussi le mot vide) sur un alphabet donné.

(2) J'ai déjà évoqué les systèmes de Lindenmayer comme un exemple d'une famille de langages transversale: elle contient quelques langages rationnels mais pas tous, quelques context-free mais pas tous, etc.--ManiacParisien (d) 7 décembre 2011 à 07:27 (CET)

(1) Un automate avec un seul état ne possède pas de condition d'arrêt et n'est donc pas réellement déterministe ; il ne s'agit pas d'un accepteur de langage permettant de résoudre le problème de la décision de l'appartenance d'un mot au langage. Au mieux, nous avons le mot vide et tous les mots infinis. Mais le vrai problème c'est que s'il lit le mot sur un ruban, comment distingue t'il l'absence de symbole de la présence d'un symbole ? Il faut un symbole pour signifier le vide, voilà le problème ; l'absence de symbole doit-être considéré comme un symbole, comme les espaces dans cette phrase (caractère ASCII 32).

(2) Comme je le répète, les L-Systèmes sont Turing-Complets (la version simultanée, séquentielle, déteministe ou non-déterministe) ; la démonstration se base sur les systèmes de Markov. S'il existait un système transveral, la hiérarchie de Chomsky disparaitrait des manuels.

Revenons à nos moutons

Wikipedia est une encyclopédie destinée au lecteur de bonne volonté. Moins de botanique, moins de byzantinisme, et 3 mots sur les rapports au réel, et sur l'utilité...

classe 4 (oubliée): langages énumérés (codes au sens le plus faible)

classe 3 : expressions "régulières" mélangeant parties énumérées et parties itérées ; comprend par exemple l'écriture des constantes numériques, les éléments de lexique(s), certains langages de commande simples ;

classe 2 : expressions plus ou moins parenthésées, sans enchevêtrement, comme par exemple les expressions algébriques ;le traitement de la classe 2 par automate à pile est bien connu ;

• pourrait s'appliquer à un programme vu comme une suite séquencée d'instructions dans laquelle les procédures, les blocs, les boucles... jouent le rôle de parenthèses ; l'enseignement de la programmation suppose souvent, depuis Algol 60, les langages de programmation dans cette classe -- c'est hélas une fiction pédagogique : aucun langage de programmation réel n'est en classe 2, et même un outil comme yacc est insuffisant pour analyser C ;
• en langue naturelle, les propositions incises jouent le rôle de parenthèses ; les propositions relatives le peuvent, mais posent des problèmes de fermeture ; enfin, cette classe interdisant l'enchevêtrement, suppose que l'on écrit "les oiseaux, les vaches et les poulains gambadaient, broutaient et chantaient" (modèle parenthétique "abcCBA")...

classe 1 : expressions à "structure de recopie" i.e. enchevêtrée ; alors on accepte "les oiseaux, les vaches et les poulains chantaient, broutaient et gambadaient", modèle à recopie "abcABC" ; plus difficile à traiter.

classe 0 : classe-limite, se divise en ce que l'informatique arrive encore à reconnaître, puis en ce qu'elle arrive encore à engendrer ; classe la plus étendue et la plus difficile à traiter.

Pour conclure, pour leur propre sécurité, je ne souhaite pas aux théoriciens que leur ascenseur soit régi par un "automate non déterministe" !

Mais je souhaite une révision concrète voire utilitariste du texte, plus motivante pour le lecteur curieux.

--Lf69100 20 avril 2013 à 19:38 (CEST)

Moins formel

J'aimerai bien que l'article soit moins formel. Un lecteur non mathématicien n'y comprend rien du tout. Là, on est obligé de se référer aux notations (les ensembles N, T, V, etc.). Ca ressemble beaucoup à un cours. On pourrait expliquer les concepts avec des phrases. Le style serait plus encyclopédique. Qu'en pensez-vous ? --Fschwarzentruber (discuter) 26 septembre 2016 à 13:53 (CEST)

D’accord. Cette simple page a déjà fait couler beaucoup d’encre. -- ManiacParisien (discuter) 26 septembre 2016 à 14:54 (CEST)

C au lieu de L

Des classes de langage qui s'appellent L... c'est très confus. Vaut mieux les appeler C... . Non ? --Fschwarzentruber (discuter) 28 septembre 2016 à 17:15 (CEST)

J'ai éludé la question en supprimant la notation qui n'est pas utile. Cela dit, « tout le monde » écrit L... -- ManiacParisien (discuter) 29 septembre 2016 à 07:31 (CEST)

Origine de la hiérarchie de Chomsky : 1956 ?

Ce texte indique que la hiérarchie de Chomsky a été décrite par Chomsky en 1956, dans un article intitulé Three models for the description of language. L'article cité n'utilise pas le terme de hiérarchie et ne parle d'ailleurs pas des quatre classes de base de la hiérarchie de Chomsky, mais argumente pour l'utilisation de grammaires transformationnelles (formalisme prouvé depuis équivalente au type 0 ; dans un papier de Peters et Ritchie en 1971, si je ne me trompe pas). La date, ou en tout cas la référence ne me semble donc pas appropriée (je pense que cette information a été reprise de l'article anglais). --Timothée M.R. Bernard (discuter) 2 novembre 2021 à 16:46 (CET)

Bien d'accord, l'article de 1956 ne mentionne pas les trois types, même s'il parle de différentes classes. J'ai modifié le RI en ce sens, je vais aussi mettre en forme les références. --ManiacParisien (discuter) 18 novembre 2021 à 08:55 (CET)

J'ai mis en forme la biblio, mais je n'ai pas changé le texte. -- ManiacParisien (discuter) 18 novembre 2021 à 10:31 (CET)